Lambda Learner: Fast Incremental Learning on Data Streams

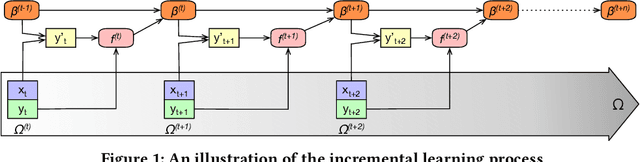
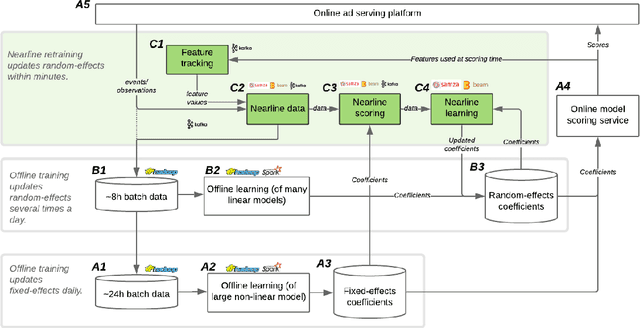
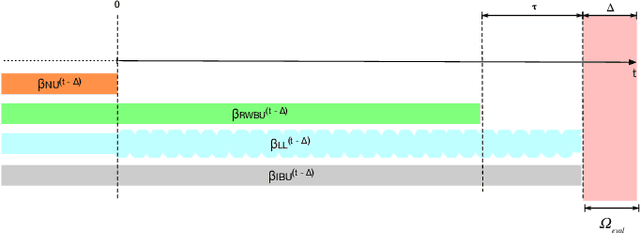
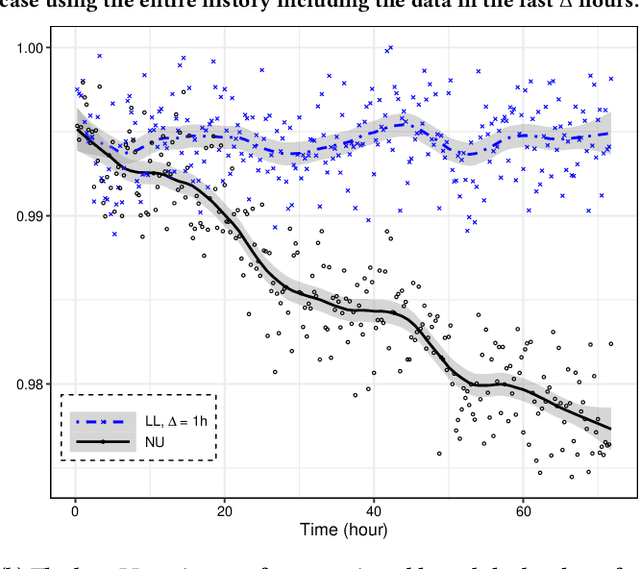
One of the most well-established applications of machine learning is in deciding what content to show website visitors. When observation data comes from high-velocity, user-generated data streams, machine learning methods perform a balancing act between model complexity, training time, and computational costs. Furthermore, when model freshness is critical, the training of models becomes time-constrained. Parallelized batch offline training, although horizontally scalable, is often not time-considerate or cost-effective. In this paper, we propose Lambda Learner, a new framework for training models by incremental updates in response to mini-batches from data streams. We show that the resulting model of our framework closely estimates a periodically updated model trained on offline data and outperforms it when model updates are time-sensitive. We provide theoretical proof that the incremental learning updates improve the loss-function over a stale batch model. We present a large-scale deployment on the sponsored content platform for a large social network, serving hundreds of millions of users across different channels (e.g., desktop, mobile). We address challenges and complexities from both algorithms and infrastructure perspectives, and illustrate the system details for computation, storage, and streaming production of training data.

Optimization Methods for Sparse Pseudo-Likelihood Graphical Model Selection

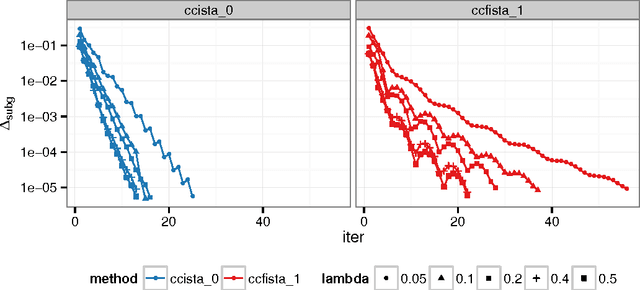
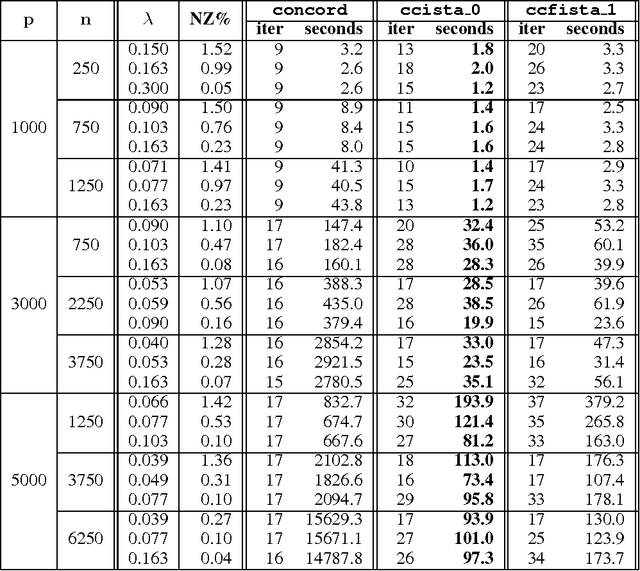
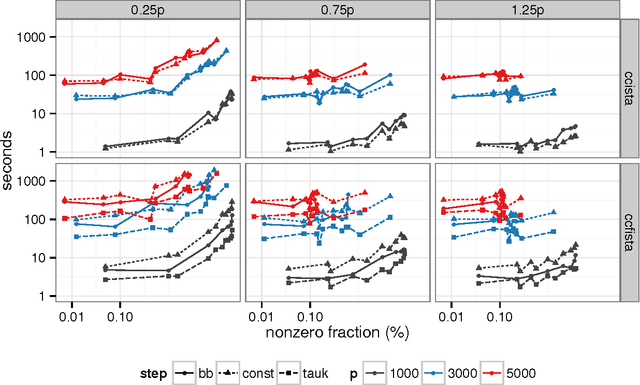
Sparse high dimensional graphical model selection is a popular topic in contemporary machine learning. To this end, various useful approaches have been proposed in the context of $\ell_1$-penalized estimation in the Gaussian framework. Though many of these inverse covariance estimation approaches are demonstrably scalable and have leveraged recent advances in convex optimization, they still depend on the Gaussian functional form. To address this gap, a convex pseudo-likelihood based partial correlation graph estimation method (CONCORD) has been recently proposed. This method uses coordinate-wise minimization of a regression based pseudo-likelihood, and has been shown to have robust model selection properties in comparison with the Gaussian approach. In direct contrast to the parallel work in the Gaussian setting however, this new convex pseudo-likelihood framework has not leveraged the extensive array of methods that have been proposed in the machine learning literature for convex optimization. In this paper, we address this crucial gap by proposing two proximal gradient methods (CONCORD-ISTA and CONCORD-FISTA) for performing $\ell_1$-regularized inverse covariance matrix estimation in the pseudo-likelihood framework. We present timing comparisons with coordinate-wise minimization and demonstrate that our approach yields tremendous payoffs for $\ell_1$-penalized partial correlation graph estimation outside the Gaussian setting, thus yielding the fastest and most scalable approach for such problems. We undertake a theoretical analysis of our approach and rigorously demonstrate convergence, and also derive rates thereof.

G-AMA: Sparse Gaussian graphical model estimation via alternating minimization

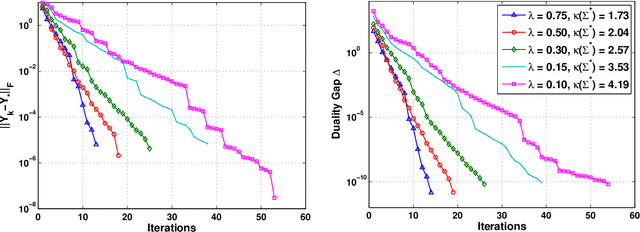
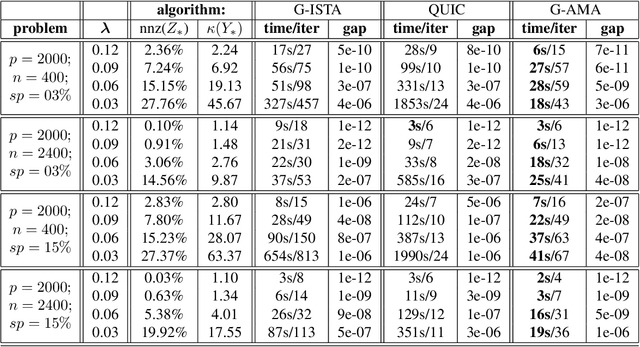
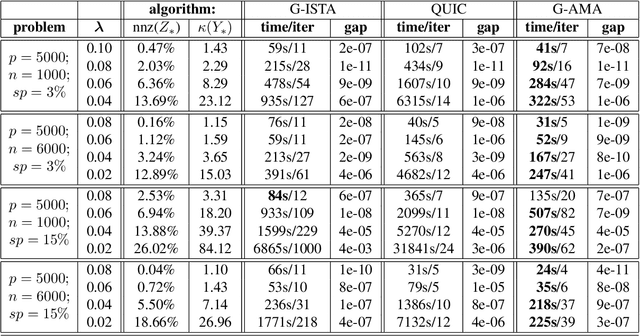
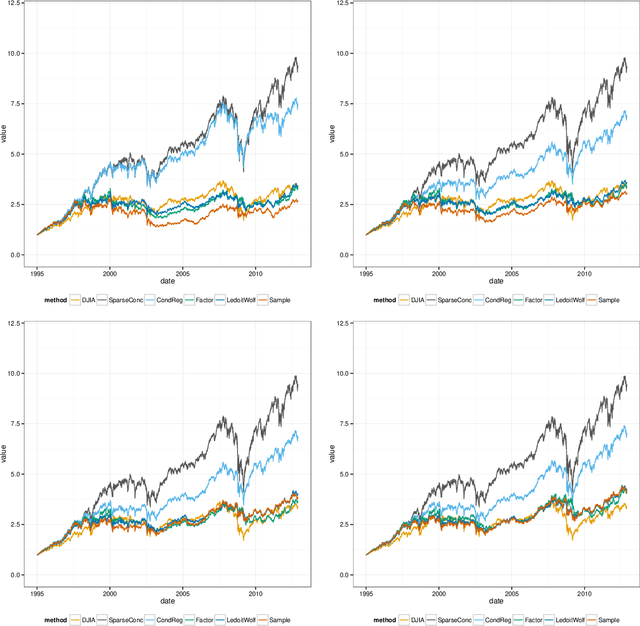
Several methods have been recently proposed for estimating sparse Gaussian graphical models using $\ell_{1}$ regularization on the inverse covariance matrix. Despite recent advances, contemporary applications require methods that are even faster in order to handle ill-conditioned high dimensional modern day datasets. In this paper, we propose a new method, G-AMA, to solve the sparse inverse covariance estimation problem using Alternating Minimization Algorithm (AMA), that effectively works as a proximal gradient algorithm on the dual problem. Our approach has several novel advantages over existing methods. First, we demonstrate that G-AMA is faster than the previous best algorithms by many orders of magnitude and is thus an ideal approach for modern high throughput applications. Second, global linear convergence of G-AMA is demonstrated rigorously, underscoring its good theoretical properties. Third, the dual algorithm operates on the covariance matrix, and thus easily facilitates incorporating additional constraints on pairwise/marginal relationships between feature pairs based on domain specific knowledge. Over and above estimating a sparse inverse covariance matrix, we also illustrate how to (1) incorporate constraints on the (bivariate) correlations and, (2) incorporate equality (equisparsity) or linear constraints between individual inverse covariance elements. Fourth, we also show that G-AMA is better adept at handling extremely ill-conditioned problems, as is often the case with real data. The methodology is demonstrated on both simulated and real datasets to illustrate its superior performance over recently proposed methods.