Optimization Methods for Sparse Pseudo-Likelihood Graphical Model Selection

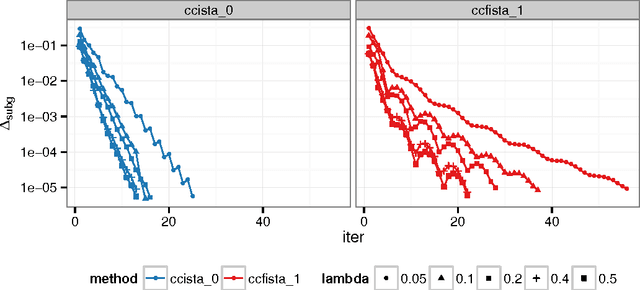
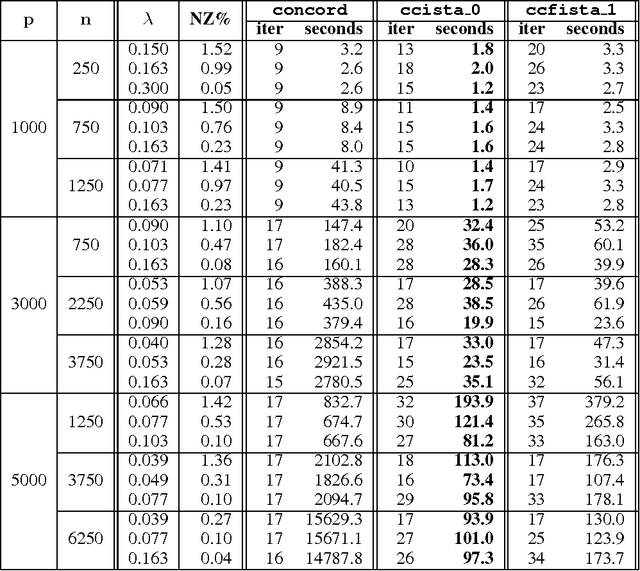
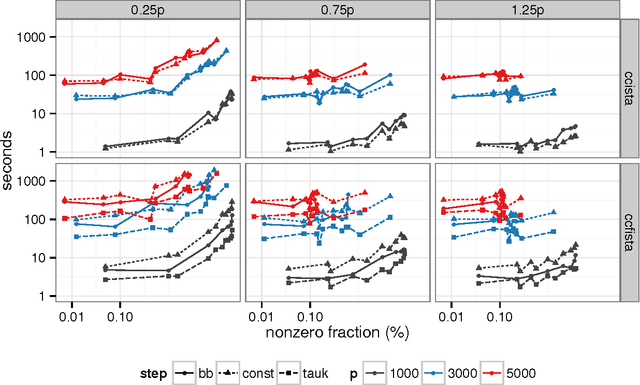
Sparse high dimensional graphical model selection is a popular topic in contemporary machine learning. To this end, various useful approaches have been proposed in the context of $\ell_1$-penalized estimation in the Gaussian framework. Though many of these inverse covariance estimation approaches are demonstrably scalable and have leveraged recent advances in convex optimization, they still depend on the Gaussian functional form. To address this gap, a convex pseudo-likelihood based partial correlation graph estimation method (CONCORD) has been recently proposed. This method uses coordinate-wise minimization of a regression based pseudo-likelihood, and has been shown to have robust model selection properties in comparison with the Gaussian approach. In direct contrast to the parallel work in the Gaussian setting however, this new convex pseudo-likelihood framework has not leveraged the extensive array of methods that have been proposed in the machine learning literature for convex optimization. In this paper, we address this crucial gap by proposing two proximal gradient methods (CONCORD-ISTA and CONCORD-FISTA) for performing $\ell_1$-regularized inverse covariance matrix estimation in the pseudo-likelihood framework. We present timing comparisons with coordinate-wise minimization and demonstrate that our approach yields tremendous payoffs for $\ell_1$-penalized partial correlation graph estimation outside the Gaussian setting, thus yielding the fastest and most scalable approach for such problems. We undertake a theoretical analysis of our approach and rigorously demonstrate convergence, and also derive rates thereof.