Easily parallelizable and distributable class of algorithms for structured sparsity, with optimal acceleration

Many statistical learning problems can be posed as minimization of a sum of two convex functions, one typically a composition of non-smooth and linear functions. Examples include regression under structured sparsity assumptions. Popular algorithms for solving such problems, e.g., ADMM, often involve non-trivial optimization subproblems or smoothing approximation. We consider two classes of primal-dual algorithms that do not incur these difficulties, and unify them from a perspective of monotone operator theory. From this unification we propose a continuum of preconditioned forward-backward operator splitting algorithms amenable to parallel and distributed computing. For the entire region of convergence of the whole continuum of algorithms, we establish its rates of convergence. For some known instances of this continuum, our analysis closes the gap in theory. We further exploit the unification to propose a continuum of accelerated algorithms. We show that the whole continuum attains the theoretically optimal rate of convergence. The scalability of the proposed algorithms, as well as their convergence behavior, is demonstrated up to 1.2 million variables with a distributed implementation.

Revealing Fundamental Physics from the Daya Bay Neutrino Experiment using Deep Neural Networks

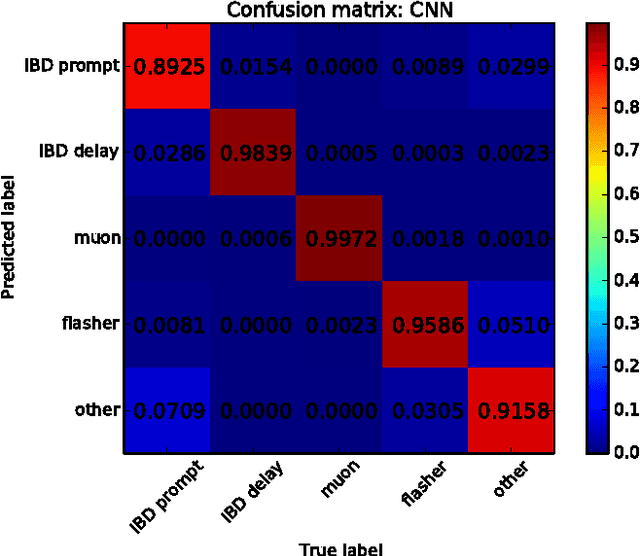
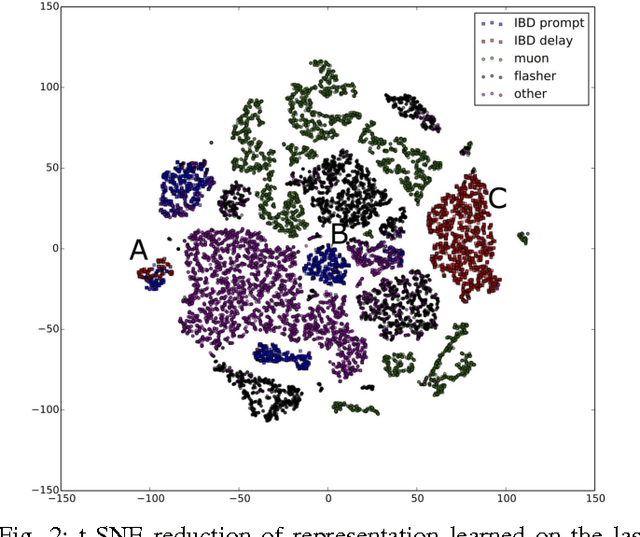
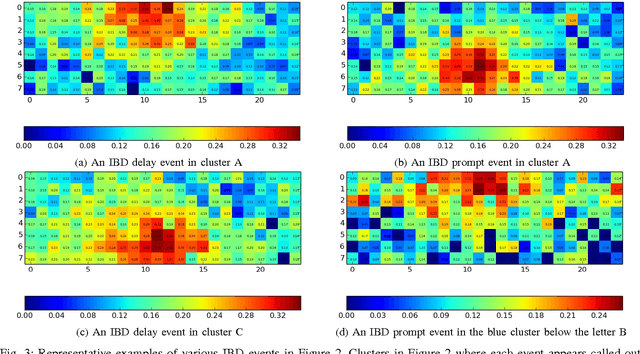
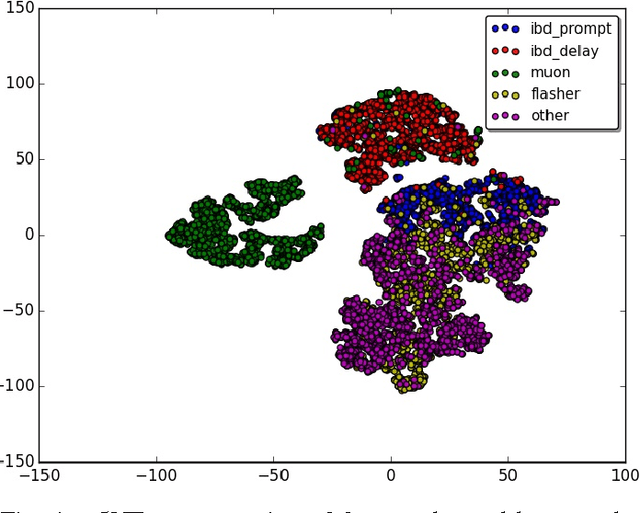
Experiments in particle physics produce enormous quantities of data that must be analyzed and interpreted by teams of physicists. This analysis is often exploratory, where scientists are unable to enumerate the possible types of signal prior to performing the experiment. Thus, tools for summarizing, clustering, visualizing and classifying high-dimensional data are essential. In this work, we show that meaningful physical content can be revealed by transforming the raw data into a learned high-level representation using deep neural networks, with measurements taken at the Daya Bay Neutrino Experiment as a case study. We further show how convolutional deep neural networks can provide an effective classification filter with greater than 97% accuracy across different classes of physics events, significantly better than other machine learning approaches.