Learning Massive-scale Partial Correlation Networks in Clinical Multi-omics Studies with HP-ACCORD

Graphical model estimation from modern multi-omics data requires a balance between statistical estimation performance and computational scalability. We introduce a novel pseudolikelihood-based graphical model framework that reparameterizes the target precision matrix while preserving sparsity pattern and estimates it by minimizing an $\ell_1$-penalized empirical risk based on a new loss function. The proposed estimator maintains estimation and selection consistency in various metrics under high-dimensional assumptions. The associated optimization problem allows for a provably fast computation algorithm using a novel operator-splitting approach and communication-avoiding distributed matrix multiplication. A high-performance computing implementation of our framework was tested in simulated data with up to one million variables demonstrating complex dependency structures akin to biological networks. Leveraging this scalability, we estimated partial correlation network from a dual-omic liver cancer data set. The co-expression network estimated from the ultrahigh-dimensional data showed superior specificity in prioritizing key transcription factors and co-activators by excluding the impact of epigenomic regulation, demonstrating the value of computational scalability in multi-omic data analysis. %derived from the gene expression data.

On the Correctness of the Generalized Isotonic Recursive Partitioning Algorithm

This paper presents an in-depth analysis of the generalized isotonic recursive partitioning (GIRP) algorithm for fitting isotonic models under separable convex losses, proposed by Luss and Rosset [J. Comput. Graph. Statist., 23 (2014), pp. 192--201] for differentiable losses and extended by Painsky and Rosset [IEEE Trans. Pattern Anal. Mach. Intell., 38 (2016), pp. 308-321] for nondifferentiable losses. The GIRP algorithm poseses an attractive feature that in each step of the algorithm, the intermediate solution satisfies the isotonicity constraint. The paper begins with an example showing that the GIRP algorithm as described in the literature may fail to produce an isotonic model, suggesting that the existence and uniqueness of the solution to the isotonic regression problem must be carefully addressed. It proceeds with showing that, among possibly many solutions, there indeed exists a solution that can be found by recursive binary partitioning of the set of observed data. A small modification of the GIRP algorithm suffices to obtain a correct solution and preserve the desired property that all the intermediate solutions are isotonic. This proposed modification includes a proper choice of intermediate solutions and a simplification of the partitioning step from ternary to binary.

$t^3$-Variational Autoencoder: Learning Heavy-tailed Data with Student's t and Power Divergence

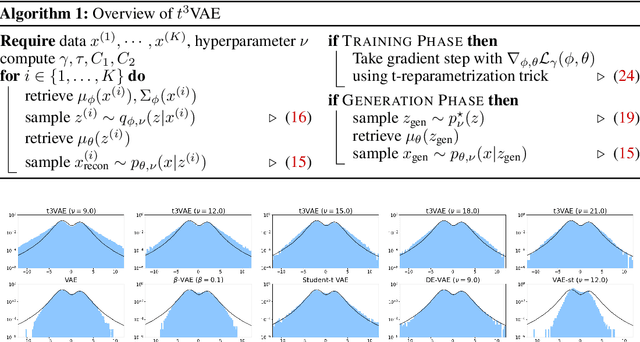
The variational autoencoder (VAE) typically employs a standard normal prior as a regularizer for the probabilistic latent encoder. However, the Gaussian tail often decays too quickly to effectively accommodate the encoded points, failing to preserve crucial structures hidden in the data. In this paper, we explore the use of heavy-tailed models to combat over-regularization. Drawing upon insights from information geometry, we propose $t^3$VAE, a modified VAE framework that incorporates Student's t-distributions for the prior, encoder, and decoder. This results in a joint model distribution of a power form which we argue can better fit real-world datasets. We derive a new objective by reformulating the evidence lower bound as joint optimization of KL divergence between two statistical manifolds and replacing with $\gamma$-power divergence, a natural alternative for power families. $t^3$VAE demonstrates superior generation of low-density regions when trained on heavy-tailed synthetic data. Furthermore, we show that $t^3$VAE significantly outperforms other models on CelebA and imbalanced CIFAR-100 datasets.

Wasserstein Geodesic Generator for Conditional Distributions

Generating samples given a specific label requires estimating conditional distributions. We derive a tractable upper bound of the Wasserstein distance between conditional distributions to lay the theoretical groundwork to learn conditional distributions. Based on this result, we propose a novel conditional generation algorithm where conditional distributions are fully characterized by a metric space defined by a statistical distance. We employ optimal transport theory to propose the Wasserstein geodesic generator, a new conditional generator that learns the Wasserstein geodesic. The proposed method learns both conditional distributions for observed domains and optimal transport maps between them. The conditional distributions given unobserved intermediate domains are on the Wasserstein geodesic between conditional distributions given two observed domain labels. Experiments on face images with light conditions as domain labels demonstrate the efficacy of the proposed method.

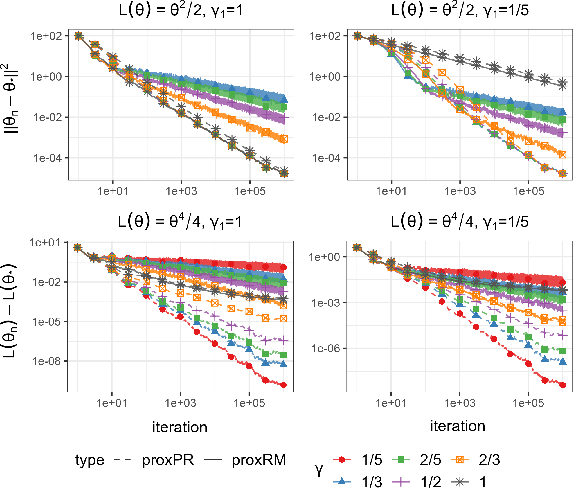
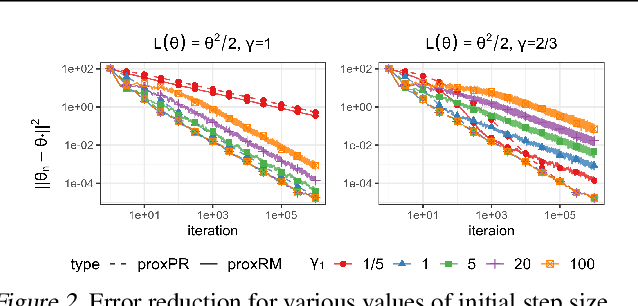
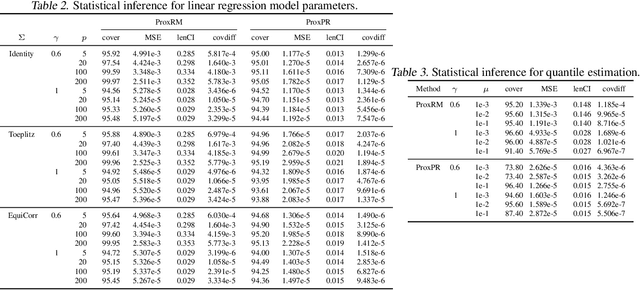
Statistical inference with implicit SGD: proximal Robbins-Monro vs. Polyak-Ruppert

The implicit stochastic gradient descent (ISGD), a proximal version of SGD, is gaining interest in the literature due to its stability over (explicit) SGD. In this paper, we conduct an in-depth analysis of the two modes of ISGD for smooth convex functions, namely proximal Robbins-Monro (proxRM) and proximal Poylak-Ruppert (proxPR) procedures, for their use in statistical inference on model parameters. Specifically, we derive non-asymptotic point estimation error bounds of both proxRM and proxPR iterates and their limiting distributions, and propose on-line estimators of their asymptotic covariance matrices that require only a single run of ISGD. The latter estimators are used to construct valid confidence intervals for the model parameters. Our analysis is free of the generalized linear model assumption that has limited the preceding analyses, and employs feasible procedures. Our on-line covariance matrix estimators appear to be the first of this kind in the ISGD literature.

Principled learning method for Wasserstein distributionally robust optimization with local perturbations

Wasserstein distributionally robust optimization (WDRO) attempts to learn a model that minimizes the local worst-case risk in the vicinity of the empirical data distribution defined by Wasserstein ball. While WDRO has received attention as a promising tool for inference since its introduction, its theoretical understanding has not been fully matured. Gao et al. (2017) proposed a minimizer based on a tractable approximation of the local worst-case risk, but without showing risk consistency. In this paper, we propose a minimizer based on a novel approximation theorem and provide the corresponding risk consistency results. Furthermore, we develop WDRO inference for locally perturbed data that include the Mixup (Zhang et al., 2017) as a special case. We show that our approximation and risk consistency results naturally extend to the cases when data are locally perturbed. Numerical experiments demonstrate robustness of the proposed method using image classification datasets. Our results show that the proposed method achieves significantly higher accuracy than baseline models on noisy datasets.

Easily parallelizable and distributable class of algorithms for structured sparsity, with optimal acceleration

Many statistical learning problems can be posed as minimization of a sum of two convex functions, one typically a composition of non-smooth and linear functions. Examples include regression under structured sparsity assumptions. Popular algorithms for solving such problems, e.g., ADMM, often involve non-trivial optimization subproblems or smoothing approximation. We consider two classes of primal-dual algorithms that do not incur these difficulties, and unify them from a perspective of monotone operator theory. From this unification we propose a continuum of preconditioned forward-backward operator splitting algorithms amenable to parallel and distributed computing. For the entire region of convergence of the whole continuum of algorithms, we establish its rates of convergence. For some known instances of this continuum, our analysis closes the gap in theory. We further exploit the unification to propose a continuum of accelerated algorithms. We show that the whole continuum attains the theoretically optimal rate of convergence. The scalability of the proposed algorithms, as well as their convergence behavior, is demonstrated up to 1.2 million variables with a distributed implementation.