Wasserstein Geodesic Generator for Conditional Distributions

Generating samples given a specific label requires estimating conditional distributions. We derive a tractable upper bound of the Wasserstein distance between conditional distributions to lay the theoretical groundwork to learn conditional distributions. Based on this result, we propose a novel conditional generation algorithm where conditional distributions are fully characterized by a metric space defined by a statistical distance. We employ optimal transport theory to propose the Wasserstein geodesic generator, a new conditional generator that learns the Wasserstein geodesic. The proposed method learns both conditional distributions for observed domains and optimal transport maps between them. The conditional distributions given unobserved intermediate domains are on the Wasserstein geodesic between conditional distributions given two observed domain labels. Experiments on face images with light conditions as domain labels demonstrate the efficacy of the proposed method.

Covariate-informed Representation Learning with Samplewise Optimal Identifiable Variational Autoencoders

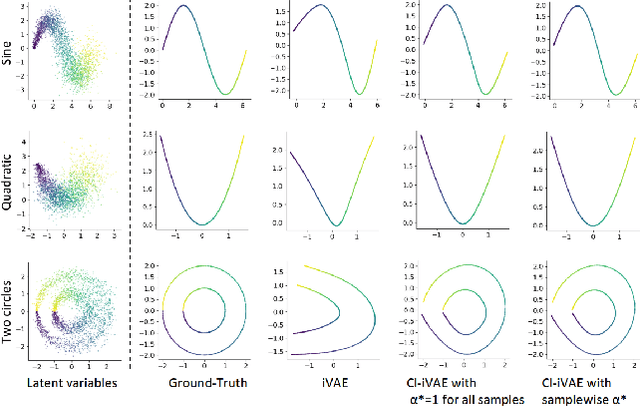
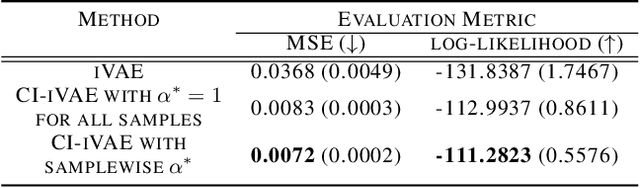
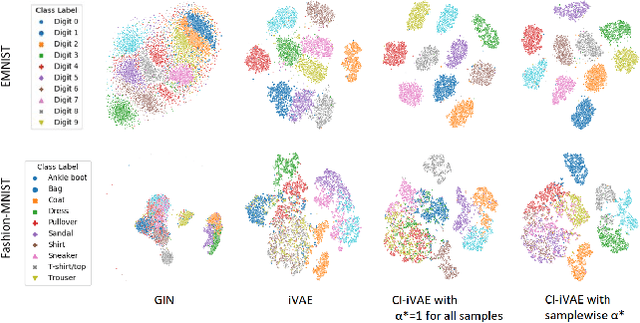
Recently proposed identifiable variational autoencoder (iVAE, Khemakhem et al. (2020)) framework provides a promising approach for learning latent independent components of the data. Although the identifiability is appealing, the objective function of iVAE does not enforce the inverse relation between encoders and decoders. Without the inverse relation, representations from the encoder in iVAE may not reconstruct observations,i.e., representations lose information in observations. To overcome this limitation, we develop a new approach, covariate-informed identifiable VAE (CI-iVAE). Different from previous iVAE implementations, our method critically leverages the posterior distribution of latent variables conditioned only on observations. In doing so, the objective function enforces the inverse relation, and learned representation contains more information of observations. Furthermore, CI-iVAE extends the original iVAE objective function to a larger class and finds the optimal one among them, thus providing a better fit to the data. Theoretically, our method has tighter evidence lower bounds (ELBOs) than the original iVAE. We demonstrate that our approach can more reliably learn features of various synthetic datasets, two benchmark image datasets (EMNIST and Fashion MNIST), and a large-scale brain imaging dataset for adolescent mental health research.

Kernel-convoluted Deep Neural Networks with Data Augmentation

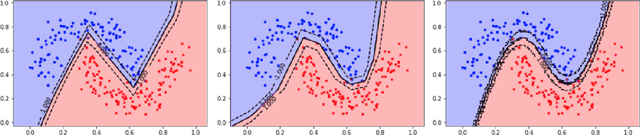
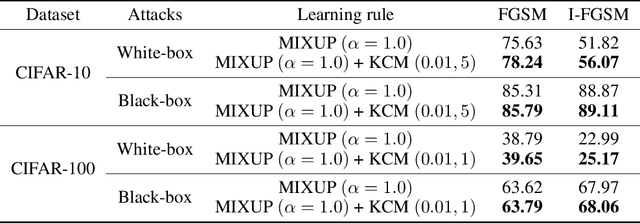
The Mixup method (Zhang et al. 2018), which uses linearly interpolated data, has emerged as an effective data augmentation tool to improve generalization performance and the robustness to adversarial examples. The motivation is to curtail undesirable oscillations by its implicit model constraint to behave linearly at in-between observed data points and promote smoothness. In this work, we formally investigate this premise, propose a way to explicitly impose smoothness constraints, and extend it to incorporate with implicit model constraints. First, we derive a new function class composed of kernel-convoluted models (KCM) where the smoothness constraint is directly imposed by locally averaging the original functions with a kernel function. Second, we propose to incorporate the Mixup method into KCM to expand the domains of smoothness. In both cases of KCM and the KCM adapted with the Mixup, we provide risk analysis, respectively, under some conditions for kernels. We show that the upper bound of the excess risk is not slower than that of the original function class. The upper bound of the KCM with the Mixup remains dominated by that of the KCM if the perturbation of the Mixup vanishes faster than \(O(n^{-1/2})\) where \(n\) is a sample size. Using CIFAR-10 and CIFAR-100 datasets, our experiments demonstrate that the KCM with the Mixup outperforms the Mixup method in terms of generalization and robustness to adversarial examples.