Doubly-Robust Off-Policy Evaluation with Estimated Logging Policy

We introduce a novel doubly-robust (DR) off-policy evaluation (OPE) estimator for Markov decision processes, DRUnknown, designed for situations where both the logging policy and the value function are unknown. The proposed estimator initially estimates the logging policy and then estimates the value function model by minimizing the asymptotic variance of the estimator while considering the estimating effect of the logging policy. When the logging policy model is correctly specified, DRUnknown achieves the smallest asymptotic variance within the class containing existing OPE estimators. When the value function model is also correctly specified, DRUnknown is optimal as its asymptotic variance reaches the semiparametric lower bound. We present experimental results conducted in contextual bandits and reinforcement learning to compare the performance of DRUnknown with that of existing methods.

Wasserstein Geodesic Generator for Conditional Distributions

Generating samples given a specific label requires estimating conditional distributions. We derive a tractable upper bound of the Wasserstein distance between conditional distributions to lay the theoretical groundwork to learn conditional distributions. Based on this result, we propose a novel conditional generation algorithm where conditional distributions are fully characterized by a metric space defined by a statistical distance. We employ optimal transport theory to propose the Wasserstein geodesic generator, a new conditional generator that learns the Wasserstein geodesic. The proposed method learns both conditional distributions for observed domains and optimal transport maps between them. The conditional distributions given unobserved intermediate domains are on the Wasserstein geodesic between conditional distributions given two observed domain labels. Experiments on face images with light conditions as domain labels demonstrate the efficacy of the proposed method.

Bandit-supported care planning for older people with complex health and care needs

Long-term care service for old people is in great demand in most of the aging societies. The number of nursing homes residents is increasing while the number of care providers is limited. Due to the care worker shortage, care to vulnerable older residents cannot be fully tailored to the unique needs and preference of each individual. This may bring negative impacts on health outcomes and quality of life among institutionalized older people. To improve care quality through personalized care planning and delivery with limited care workforce, we propose a new care planning model assisted by artificial intelligence. We apply bandit algorithms which optimize the clinical decision for care planning by adapting to the sequential feedback from the past decisions. We evaluate the proposed model on empirical data acquired from the Systems for Person-centered Elder Care (SPEC) study, a ICT-enhanced care management program.

Double Doubly Robust Thompson Sampling for Generalized Linear Contextual Bandits

We propose a novel contextual bandit algorithm for generalized linear rewards with an $\tilde{O}(\sqrt{\kappa^{-1} \phi T})$ regret over $T$ rounds where $\phi$ is the minimum eigenvalue of the covariance of contexts and $\kappa$ is a lower bound of the variance of rewards. In several practical cases where $\phi=O(d)$, our result is the first regret bound for generalized linear model (GLM) bandits with the order $\sqrt{d}$ without relying on the approach of Auer [2002]. We achieve this bound using a novel estimator called double doubly-robust (DDR) estimator, a subclass of doubly-robust (DR) estimator but with a tighter error bound. The approach of Auer [2002] achieves independence by discarding the observed rewards, whereas our algorithm achieves independence considering all contexts using our DDR estimator. We also provide an $O(\kappa^{-1} \phi \log (NT) \log T)$ regret bound for $N$ arms under a probabilistic margin condition. Regret bounds under the margin condition are given by Bastani and Bayati [2020] and Bastani et al. [2021] under the setting that contexts are common to all arms but coefficients are arm-specific. When contexts are different for all arms but coefficients are common, ours is the first regret bound under the margin condition for linear models or GLMs. We conduct empirical studies using synthetic data and real examples, demonstrating the effectiveness of our algorithm.

Squeeze All: Novel Estimator and Self-Normalized Bound for Linear Contextual Bandits

We propose a novel algorithm for linear contextual bandits with $O(\sqrt{dT \log T})$ regret bound, where $d$ is the dimension of contexts and $T$ is the time horizon. Our proposed algorithm is equipped with a novel estimator in which exploration is embedded through explicit randomization. Depending on the randomization, our proposed estimator takes contribution either from contexts of all arms or from selected contexts. We establish a self-normalized bound for our estimator, which allows a novel decomposition of the cumulative regret into additive dimension-dependent terms instead of multiplicative terms. We also prove a novel lower bound of $\Omega(\sqrt{dT})$ under our problem setting. Hence, the regret of our proposed algorithm matches the lower bound up to logarithmic factors. The numerical experiments support the theoretical guarantees and show that our proposed method outperforms the existing linear bandit algorithms.

Semi-Parametric Contextual Bandits with Graph-Laplacian Regularization

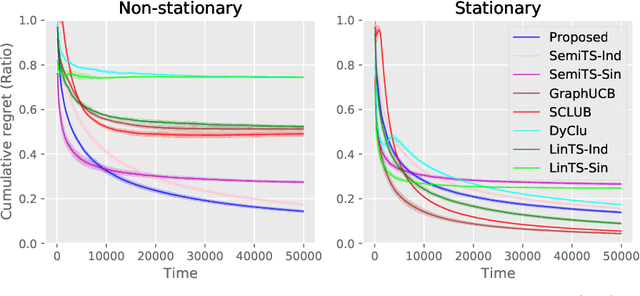
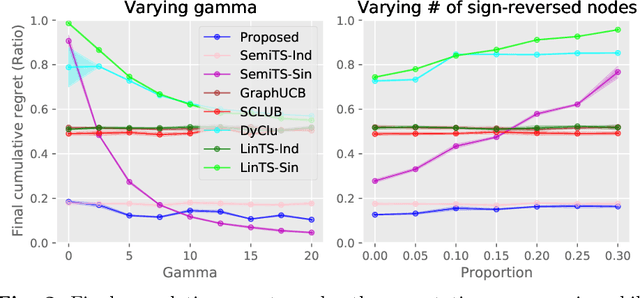
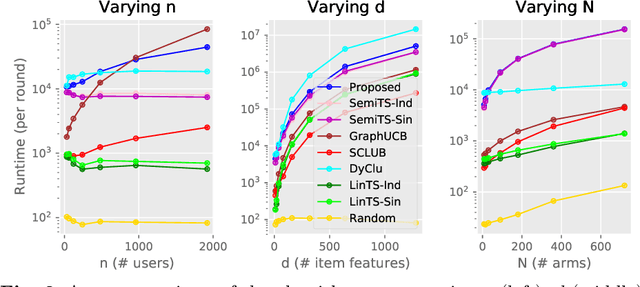
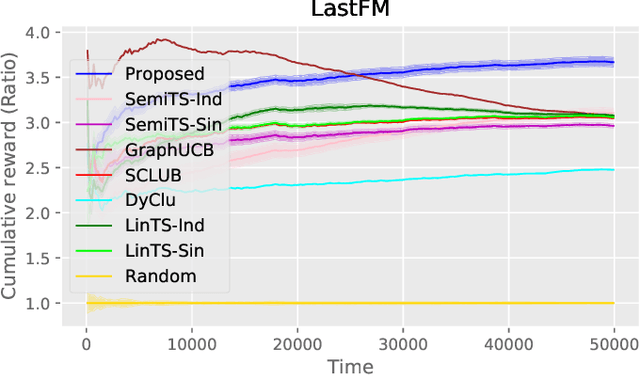
Non-stationarity is ubiquitous in human behavior and addressing it in the contextual bandits is challenging. Several works have addressed the problem by investigating semi-parametric contextual bandits and warned that ignoring non-stationarity could harm performances. Another prevalent human behavior is social interaction which has become available in a form of a social network or graph structure. As a result, graph-based contextual bandits have received much attention. In this paper, we propose "SemiGraphTS," a novel contextual Thompson-sampling algorithm for a graph-based semi-parametric reward model. Our algorithm is the first to be proposed in this setting. We derive an upper bound of the cumulative regret that can be expressed as a multiple of a factor depending on the graph structure and the order for the semi-parametric model without a graph. We evaluate the proposed and existing algorithms via simulation and real data example.

Doubly Robust Thompson Sampling for linear payoffs

A challenging aspect of the bandit problem is that a stochastic reward is observed only for the chosen arm and the rewards of other arms remain missing. Since the arm choice depends on the past context and reward pairs, the contexts of chosen arms suffer from correlation and render the analysis difficult. We propose a novel multi-armed contextual bandit algorithm called Doubly Robust (DR) Thompson Sampling (TS) that applies the DR technique used in missing data literature to TS. The proposed algorithm improves the bound of TS by a factor of $\sqrt{d}$, where $d$ is the dimension of the context. A benefit of the proposed method is that it uses all the context data, chosen or not chosen, thus allowing to circumvent the technical definition of unsaturated arms used in theoretical analysis of TS. Empirical studies show the advantage of the proposed algorithm over TS.

Kernel-convoluted Deep Neural Networks with Data Augmentation

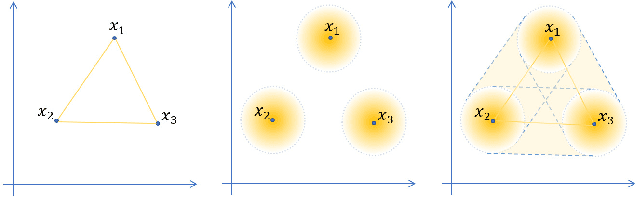
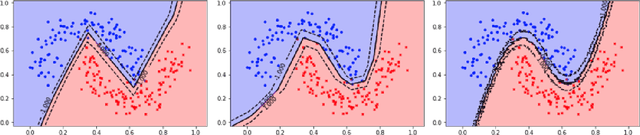
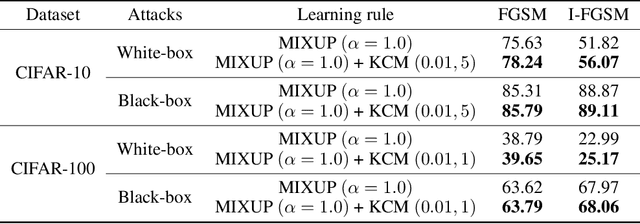
The Mixup method (Zhang et al. 2018), which uses linearly interpolated data, has emerged as an effective data augmentation tool to improve generalization performance and the robustness to adversarial examples. The motivation is to curtail undesirable oscillations by its implicit model constraint to behave linearly at in-between observed data points and promote smoothness. In this work, we formally investigate this premise, propose a way to explicitly impose smoothness constraints, and extend it to incorporate with implicit model constraints. First, we derive a new function class composed of kernel-convoluted models (KCM) where the smoothness constraint is directly imposed by locally averaging the original functions with a kernel function. Second, we propose to incorporate the Mixup method into KCM to expand the domains of smoothness. In both cases of KCM and the KCM adapted with the Mixup, we provide risk analysis, respectively, under some conditions for kernels. We show that the upper bound of the excess risk is not slower than that of the original function class. The upper bound of the KCM with the Mixup remains dominated by that of the KCM if the perturbation of the Mixup vanishes faster than \(O(n^{-1/2})\) where \(n\) is a sample size. Using CIFAR-10 and CIFAR-100 datasets, our experiments demonstrate that the KCM with the Mixup outperforms the Mixup method in terms of generalization and robustness to adversarial examples.

Principled learning method for Wasserstein distributionally robust optimization with local perturbations

Wasserstein distributionally robust optimization (WDRO) attempts to learn a model that minimizes the local worst-case risk in the vicinity of the empirical data distribution defined by Wasserstein ball. While WDRO has received attention as a promising tool for inference since its introduction, its theoretical understanding has not been fully matured. Gao et al. (2017) proposed a minimizer based on a tractable approximation of the local worst-case risk, but without showing risk consistency. In this paper, we propose a minimizer based on a novel approximation theorem and provide the corresponding risk consistency results. Furthermore, we develop WDRO inference for locally perturbed data that include the Mixup (Zhang et al., 2017) as a special case. We show that our approximation and risk consistency results naturally extend to the cases when data are locally perturbed. Numerical experiments demonstrate robustness of the proposed method using image classification datasets. Our results show that the proposed method achieves significantly higher accuracy than baseline models on noisy datasets.

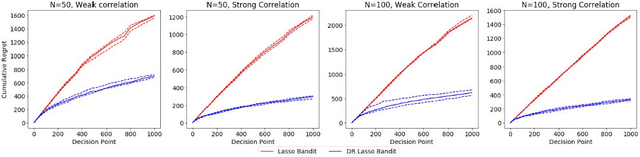
Doubly-Robust Lasso Bandit

Contextual multi-armed bandit algorithms are widely used in sequential decision tasks such as news article recommendation systems, web page ad placement algorithms, and mobile health. Most of the existing algorithms have regret proportional to a polynomial function of the context dimension, $d$. In many applications however, it is often the case that contexts are high-dimensional with only a sparse subset of size $s_0 (\ll d)$ being correlated with the reward. We propose a novel algorithm, namely the Doubly-Robust Lasso Bandit algorithm, which exploits the sparse structure as in Lasso, while blending the doubly-robust technique used in missing data literature. The high-probability upper bound of the regret incurred by the proposed algorithm does not depend on the number of arms, has better dependency on $s_0$ than previous works, and scales with $\mathrm{log}(d)$ instead of a polynomial function of $d$. The proposed algorithm shows good performance when contexts of different arms are correlated and requires less tuning parameters than existing methods.