ATLANTIS: AI-driven Threat Localization, Analysis, and Triage Intelligence System

We present ATLANTIS, the cyber reasoning system developed by Team Atlanta that won 1st place in the Final Competition of DARPA's AI Cyber Challenge (AIxCC) at DEF CON 33 (August 2025). AIxCC (2023-2025) challenged teams to build autonomous cyber reasoning systems capable of discovering and patching vulnerabilities at the speed and scale of modern software. ATLANTIS integrates large language models (LLMs) with program analysis -- combining symbolic execution, directed fuzzing, and static analysis -- to address limitations in automated vulnerability discovery and program repair. Developed by researchers at Georgia Institute of Technology, Samsung Research, KAIST, and POSTECH, the system addresses core challenges: scaling across diverse codebases from C to Java, achieving high precision while maintaining broad coverage, and producing semantically correct patches that preserve intended behavior. We detail the design philosophy, architectural decisions, and implementation strategies behind ATLANTIS, share lessons learned from pushing the boundaries of automated security when program analysis meets modern AI, and release artifacts to support reproducibility and future research.

Adaptive Data Augmentation for Thompson Sampling

In linear contextual bandits, the objective is to select actions that maximize cumulative rewards, modeled as a linear function with unknown parameters. Although Thompson Sampling performs well empirically, it does not achieve optimal regret bounds. This paper proposes a nearly minimax optimal Thompson Sampling for linear contextual bandits by developing a novel estimator with the adaptive augmentation and coupling of the hypothetical samples that are designed for efficient parameter learning. The proposed estimator accurately predicts rewards for all arms without relying on assumptions for the context distribution. Empirical results show robust performance and significant improvement over existing methods.

Linear Bandits with Partially Observable Features

We introduce a novel linear bandit problem with partially observable features, resulting in partial reward information and spurious estimates. Without proper address for latent part, regret possibly grows linearly in decision horizon $T$, as their influence on rewards are unknown. To tackle this, we propose a novel analysis to handle the latent features and an algorithm that achieves sublinear regret. The core of our algorithm involves (i) augmenting basis vectors orthogonal to the observed feature space, and (ii) introducing an efficient doubly robust estimator. Our approach achieves a regret bound of $\tilde{O}(\sqrt{(d + d_h)T})$, where $d$ is the dimension of observed features, and $d_h$ is the unknown dimension of the subspace of the unobserved features. Notably, our algorithm requires no prior knowledge of the unobserved feature space, which may expand as more features become hidden. Numerical experiments confirm that our algorithm outperforms both non-contextual multi-armed bandits and linear bandit algorithms depending solely on observed features.

A Doubly Robust Approach to Sparse Reinforcement Learning

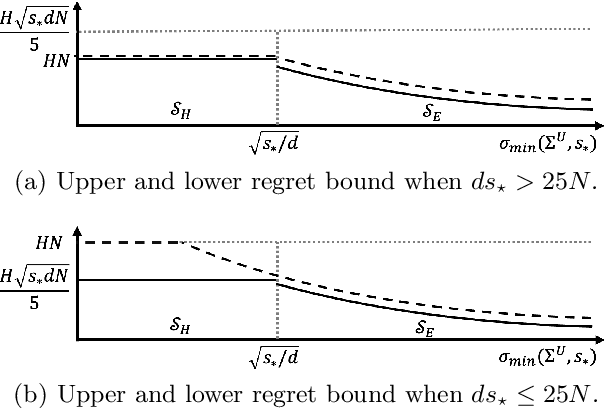
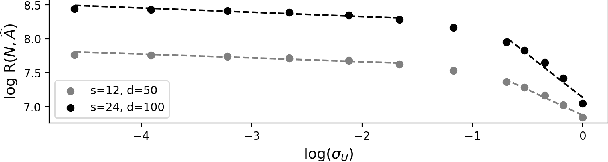
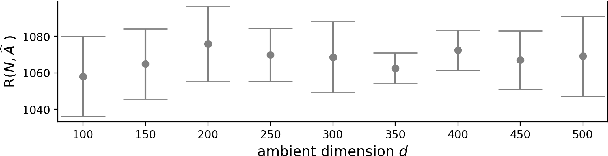
We propose a new regret minimization algorithm for episodic sparse linear Markov decision process (SMDP) where the state-transition distribution is a linear function of observed features. The only previously known algorithm for SMDP requires the knowledge of the sparsity parameter and oracle access to an unknown policy. We overcome these limitations by combining the doubly robust method that allows one to use feature vectors of \emph{all} actions with a novel analysis technique that enables the algorithm to use data from all periods in all episodes. The regret of the proposed algorithm is $\tilde{O}(\sigma^{-1}_{\min} s_{\star} H \sqrt{N})$, where $\sigma_{\min}$ denotes the restrictive the minimum eigenvalue of the average Gram matrix of feature vectors, $s_\star$ is the sparsity parameter, $H$ is the length of an episode, and $N$ is the number of rounds. We provide a lower regret bound that matches the upper bound up to logarithmic factors on a newly identified subclass of SMDPs. Our numerical experiments support our theoretical results and demonstrate the superior performance of our algorithm.

Pareto Front Identification with Regret Minimization

We consider Pareto front identification for linear bandits (PFILin) where the goal is to identify a set of arms whose reward vectors are not dominated by any of the others when the mean reward vector is a linear function of the context. PFILin includes the best arm identification problem and multi-objective active learning as special cases. The sample complexity of our proposed algorithm is $\tilde{O}(d/\Delta^2)$, where $d$ is the dimension of contexts and $\Delta$ is a measure of problem complexity. Our sample complexity is optimal up to a logarithmic factor. A novel feature of our algorithm is that it uses the contexts of all actions. In addition to efficiently identifying the Pareto front, our algorithm also guarantees $\tilde{O}(\sqrt{d/t})$ bound for instantaneous Pareto regret when the number of samples is larger than $\Omega(d\log dL)$ for $L$ dimensional vector rewards. By using the contexts of all arms, our proposed algorithm simultaneously provides efficient Pareto front identification and regret minimization. Numerical experiments demonstrate that the proposed algorithm successfully identifies the Pareto front while minimizing the regret.

Improved Algorithms for Multi-period Multi-class Packing Problems with~Bandit~Feedback

We consider the linear contextual multi-class multi-period packing problem~(LMMP) where the goal is to pack items such that the total vector of consumption is below a given budget vector and the total value is as large as possible. We consider the setting where the reward and the consumption vector associated with each action is a class-dependent linear function of the context, and the decision-maker receives bandit feedback. LMMP includes linear contextual bandits with knapsacks and online revenue management as special cases. We establish a new more efficient estimator which guarantees a faster convergence rate, and consequently, a lower regret in such problems. We propose a bandit policy that is a closed-form function of said estimated parameters. When the contexts are non-degenerate, the regret of the proposed policy is sublinear in the context dimension, the number of classes, and the time horizon~$T$ when the budget grows at least as $\sqrt{T}$. We also resolve an open problem posed in Agrawal & Devanur (2016), and extend the result to a multi-class setting. Our numerical experiments clearly demonstrate that the performance of our policy is superior to other benchmarks in the literature.

Double Doubly Robust Thompson Sampling for Generalized Linear Contextual Bandits

We propose a novel contextual bandit algorithm for generalized linear rewards with an $\tilde{O}(\sqrt{\kappa^{-1} \phi T})$ regret over $T$ rounds where $\phi$ is the minimum eigenvalue of the covariance of contexts and $\kappa$ is a lower bound of the variance of rewards. In several practical cases where $\phi=O(d)$, our result is the first regret bound for generalized linear model (GLM) bandits with the order $\sqrt{d}$ without relying on the approach of Auer [2002]. We achieve this bound using a novel estimator called double doubly-robust (DDR) estimator, a subclass of doubly-robust (DR) estimator but with a tighter error bound. The approach of Auer [2002] achieves independence by discarding the observed rewards, whereas our algorithm achieves independence considering all contexts using our DDR estimator. We also provide an $O(\kappa^{-1} \phi \log (NT) \log T)$ regret bound for $N$ arms under a probabilistic margin condition. Regret bounds under the margin condition are given by Bastani and Bayati [2020] and Bastani et al. [2021] under the setting that contexts are common to all arms but coefficients are arm-specific. When contexts are different for all arms but coefficients are common, ours is the first regret bound under the margin condition for linear models or GLMs. We conduct empirical studies using synthetic data and real examples, demonstrating the effectiveness of our algorithm.

Squeeze All: Novel Estimator and Self-Normalized Bound for Linear Contextual Bandits

We propose a novel algorithm for linear contextual bandits with $O(\sqrt{dT \log T})$ regret bound, where $d$ is the dimension of contexts and $T$ is the time horizon. Our proposed algorithm is equipped with a novel estimator in which exploration is embedded through explicit randomization. Depending on the randomization, our proposed estimator takes contribution either from contexts of all arms or from selected contexts. We establish a self-normalized bound for our estimator, which allows a novel decomposition of the cumulative regret into additive dimension-dependent terms instead of multiplicative terms. We also prove a novel lower bound of $\Omega(\sqrt{dT})$ under our problem setting. Hence, the regret of our proposed algorithm matches the lower bound up to logarithmic factors. The numerical experiments support the theoretical guarantees and show that our proposed method outperforms the existing linear bandit algorithms.

Doubly Robust Thompson Sampling for linear payoffs

A challenging aspect of the bandit problem is that a stochastic reward is observed only for the chosen arm and the rewards of other arms remain missing. Since the arm choice depends on the past context and reward pairs, the contexts of chosen arms suffer from correlation and render the analysis difficult. We propose a novel multi-armed contextual bandit algorithm called Doubly Robust (DR) Thompson Sampling (TS) that applies the DR technique used in missing data literature to TS. The proposed algorithm improves the bound of TS by a factor of $\sqrt{d}$, where $d$ is the dimension of the context. A benefit of the proposed method is that it uses all the context data, chosen or not chosen, thus allowing to circumvent the technical definition of unsaturated arms used in theoretical analysis of TS. Empirical studies show the advantage of the proposed algorithm over TS.

Principled learning method for Wasserstein distributionally robust optimization with local perturbations

Wasserstein distributionally robust optimization (WDRO) attempts to learn a model that minimizes the local worst-case risk in the vicinity of the empirical data distribution defined by Wasserstein ball. While WDRO has received attention as a promising tool for inference since its introduction, its theoretical understanding has not been fully matured. Gao et al. (2017) proposed a minimizer based on a tractable approximation of the local worst-case risk, but without showing risk consistency. In this paper, we propose a minimizer based on a novel approximation theorem and provide the corresponding risk consistency results. Furthermore, we develop WDRO inference for locally perturbed data that include the Mixup (Zhang et al., 2017) as a special case. We show that our approximation and risk consistency results naturally extend to the cases when data are locally perturbed. Numerical experiments demonstrate robustness of the proposed method using image classification datasets. Our results show that the proposed method achieves significantly higher accuracy than baseline models on noisy datasets.