Model-Free Approximate Bayesian Learning for Large-Scale Conversion Funnel Optimization

The flexibility of choosing the ad action as a function of the consumer state is critical for modern-day marketing campaigns. We study the problem of identifying the optimal sequential personalized interventions that maximize the adoption probability for a new product. We model consumer behavior by a conversion funnel that captures the state of each consumer (e.g., interaction history with the firm) and allows the consumer behavior to vary as a function of both her state and firm's sequential interventions. We show our model captures consumer behavior with very high accuracy (out-of-sample AUC of over 0.95) in a real-world email marketing dataset. However, it results in a very large-scale learning problem, where the firm must learn the state-specific effects of various interventions from consumer interactions. We propose a novel attribution-based decision-making algorithm for this problem that we call model-free approximate Bayesian learning. Our algorithm inherits the interpretability and scalability of Thompson sampling for bandits and maintains an approximate belief over the value of each state-specific intervention. The belief is updated as the algorithm interacts with the consumers. Despite being an approximation to the Bayes update, we prove the asymptotic optimality of our algorithm and analyze its convergence rate. We show that our algorithm significantly outperforms traditional approaches on extensive simulations calibrated to a real-world email marketing dataset.

A Doubly Robust Approach to Sparse Reinforcement Learning

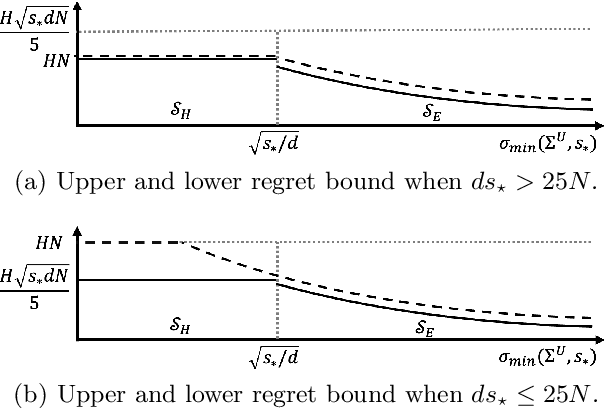
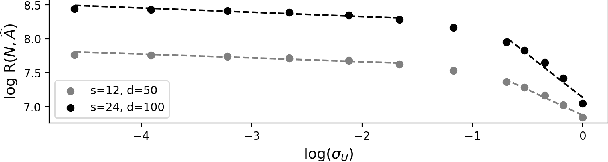
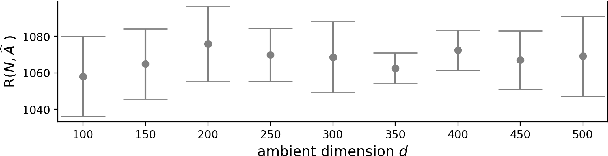
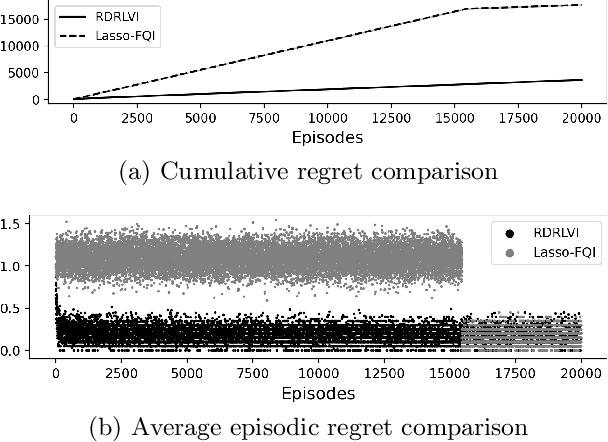
We propose a new regret minimization algorithm for episodic sparse linear Markov decision process (SMDP) where the state-transition distribution is a linear function of observed features. The only previously known algorithm for SMDP requires the knowledge of the sparsity parameter and oracle access to an unknown policy. We overcome these limitations by combining the doubly robust method that allows one to use feature vectors of \emph{all} actions with a novel analysis technique that enables the algorithm to use data from all periods in all episodes. The regret of the proposed algorithm is $\tilde{O}(\sigma^{-1}_{\min} s_{\star} H \sqrt{N})$, where $\sigma_{\min}$ denotes the restrictive the minimum eigenvalue of the average Gram matrix of feature vectors, $s_\star$ is the sparsity parameter, $H$ is the length of an episode, and $N$ is the number of rounds. We provide a lower regret bound that matches the upper bound up to logarithmic factors on a newly identified subclass of SMDPs. Our numerical experiments support our theoretical results and demonstrate the superior performance of our algorithm.

Scalable Computation of Causal Bounds

We consider the problem of computing bounds for causal queries on causal graphs with unobserved confounders and discrete valued observed variables, where identifiability does not hold. Existing non-parametric approaches for computing such bounds use linear programming (LP) formulations that quickly become intractable for existing solvers because the size of the LP grows exponentially in the number of edges in the causal graph. We show that this LP can be significantly pruned, allowing us to compute bounds for significantly larger causal inference problems compared to existing techniques. This pruning procedure allows us to compute bounds in closed form for a special class of problems, including a well-studied family of problems where multiple confounded treatments influence an outcome. We extend our pruning methodology to fractional LPs which compute bounds for causal queries which incorporate additional observations about the unit. We show that our methods provide significant runtime improvement compared to benchmarks in experiments and extend our results to the finite data setting. For causal inference without additional observations, we propose an efficient greedy heuristic that produces high quality bounds, and scales to problems that are several orders of magnitude larger than those for which the pruned LP can be solved.

Optimizer's Information Criterion: Dissecting and Correcting Bias in Data-Driven Optimization

In data-driven optimization, the sample performance of the obtained decision typically incurs an optimistic bias against the true performance, a phenomenon commonly known as the Optimizer's Curse and intimately related to overfitting in machine learning. Common techniques to correct this bias, such as cross-validation, require repeatedly solving additional optimization problems and are therefore computationally expensive. We develop a general bias correction approach, building on what we call Optimizer's Information Criterion (OIC), that directly approximates the first-order bias and does not require solving any additional optimization problems. Our OIC generalizes the celebrated Akaike Information Criterion to evaluate the objective performance in data-driven optimization, which crucially involves not only model fitting but also its interplay with the downstream optimization. As such it can be used for decision selection instead of only model selection. We apply our approach to a range of data-driven optimization formulations comprising empirical and parametric models, their regularized counterparts, and furthermore contextual optimization. Finally, we provide numerical validation on the superior performance of our approach under synthetic and real-world datasets.

Pareto Front Identification with Regret Minimization

We consider Pareto front identification for linear bandits (PFILin) where the goal is to identify a set of arms whose reward vectors are not dominated by any of the others when the mean reward vector is a linear function of the context. PFILin includes the best arm identification problem and multi-objective active learning as special cases. The sample complexity of our proposed algorithm is $\tilde{O}(d/\Delta^2)$, where $d$ is the dimension of contexts and $\Delta$ is a measure of problem complexity. Our sample complexity is optimal up to a logarithmic factor. A novel feature of our algorithm is that it uses the contexts of all actions. In addition to efficiently identifying the Pareto front, our algorithm also guarantees $\tilde{O}(\sqrt{d/t})$ bound for instantaneous Pareto regret when the number of samples is larger than $\Omega(d\log dL)$ for $L$ dimensional vector rewards. By using the contexts of all arms, our proposed algorithm simultaneously provides efficient Pareto front identification and regret minimization. Numerical experiments demonstrate that the proposed algorithm successfully identifies the Pareto front while minimizing the regret.

Improved Algorithms for Multi-period Multi-class Packing Problems with~Bandit~Feedback

We consider the linear contextual multi-class multi-period packing problem~(LMMP) where the goal is to pack items such that the total vector of consumption is below a given budget vector and the total value is as large as possible. We consider the setting where the reward and the consumption vector associated with each action is a class-dependent linear function of the context, and the decision-maker receives bandit feedback. LMMP includes linear contextual bandits with knapsacks and online revenue management as special cases. We establish a new more efficient estimator which guarantees a faster convergence rate, and consequently, a lower regret in such problems. We propose a bandit policy that is a closed-form function of said estimated parameters. When the contexts are non-degenerate, the regret of the proposed policy is sublinear in the context dimension, the number of classes, and the time horizon~$T$ when the budget grows at least as $\sqrt{T}$. We also resolve an open problem posed in Agrawal & Devanur (2016), and extend the result to a multi-class setting. Our numerical experiments clearly demonstrate that the performance of our policy is superior to other benchmarks in the literature.

Hedging against Complexity: Distributionally Robust Optimization with Parametric Approximation

Empirical risk minimization (ERM) and distributionally robust optimization (DRO) are popular approaches for solving stochastic optimization problems that appear in operations management and machine learning. Existing generalization error bounds for these methods depend on either the complexity of the cost function or dimension of the uncertain parameters; consequently, the performance of these methods is poor for high-dimensional problems with objective functions under high complexity. We propose a simple approach in which the distribution of uncertain parameters is approximated using a parametric family of distributions. This mitigates both sources of complexity; however, it introduces a model misspecification error. We show that this new source of error can be controlled by suitable DRO formulations. Our proposed parametric DRO approach has significantly improved generalization bounds over existing ERM / DRO methods and parametric ERM for a wide variety of settings. Our method is particularly effective under distribution shifts. We also illustrate the superior performance of our approach on both synthetic and real-data portfolio optimization and regression tasks.

Multinomial Logit Contextual Bandits: Provable Optimality and Practicality

We consider a sequential assortment selection problem where the user choice is given by a multinomial logit (MNL) choice model whose parameters are unknown. In each period, the learning agent observes a $d$-dimensional contextual information about the user and the $N$ available items, and offers an assortment of size $K$ to the user, and observes the bandit feedback of the item chosen from the assortment. We propose upper confidence bound based algorithms for this MNL contextual bandit. The first algorithm is a simple and practical method which achieves an $\tilde{\mathcal{O}}(d\sqrt{T})$ regret over $T$ rounds. Next, we propose a second algorithm which achieves a $\tilde{\mathcal{O}}(\sqrt{dT})$ regret. This matches the lower bound for the MNL bandit problem, up to logarithmic terms, and improves on the best known result by a $\sqrt{d}$ factor. To establish this sharper regret bound, we present a non-asymptotic confidence bound for the maximum likelihood estimator of the MNL model that may be of independent interest as its own theoretical contribution. We then revisit the simpler, significantly more practical, first algorithm and show that a simple variant of the algorithm achieves the optimal regret for a broad class of important applications.

Sparsity-Agnostic Lasso Bandit

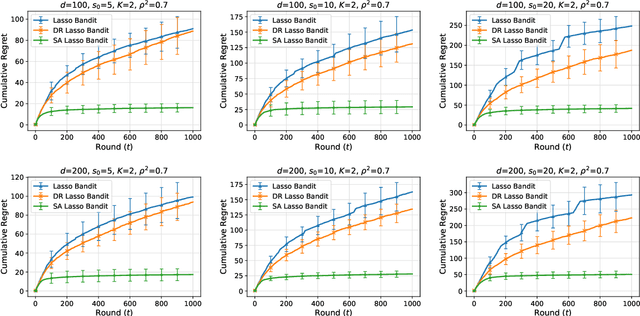
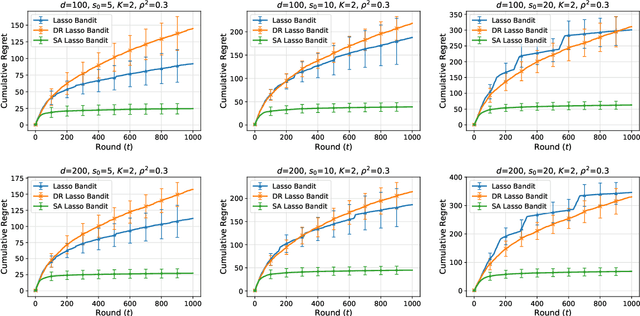
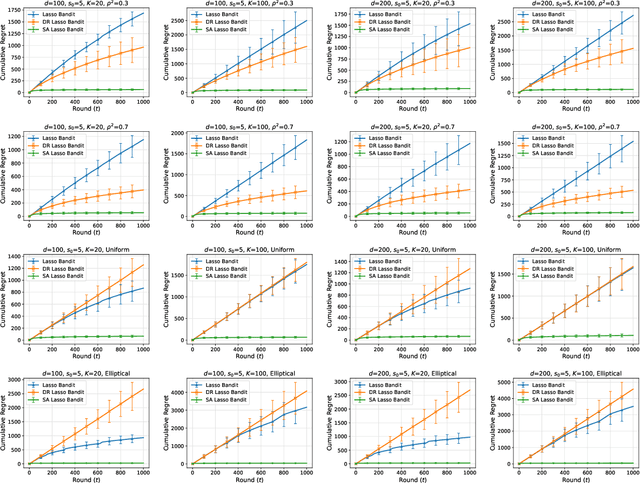
We consider a stochastic contextual bandit problem where the dimension $d$ of the feature vectors is potentially large, however, only a sparse subset of features of cardinality $s_0 \ll d$ affect the reward function. Essentially all existing algorithms for sparse bandits require a priori knowledge of the value of the sparsity index $s_0$. This knowledge is almost never available in practice, and misspecification of this parameter can lead to severe deterioration in the performance of existing methods. The main contribution of this paper is to propose an algorithm that does \emph{not} require prior knowledge of the sparsity index $s_0$ and establish tight regret bounds on its performance under mild conditions. We also comprehensively evaluate our proposed algorithm numerically and show that it consistently outperforms existing methods, even when the correct sparsity index is revealed to them but is kept hidden from our algorithm.

Sequential Anomaly Detection using Inverse Reinforcement Learning

One of the most interesting application scenarios in anomaly detection is when sequential data are targeted. For example, in a safety-critical environment, it is crucial to have an automatic detection system to screen the streaming data gathered by monitoring sensors and to report abnormal observations if detected in real-time. Oftentimes, stakes are much higher when these potential anomalies are intentional or goal-oriented. We propose an end-to-end framework for sequential anomaly detection using inverse reinforcement learning (IRL), whose objective is to determine the decision-making agent's underlying function which triggers his/her behavior. The proposed method takes the sequence of actions of a target agent (and possibly other meta information) as input. The agent's normal behavior is then understood by the reward function which is inferred via IRL. We use a neural network to represent a reward function. Using a learned reward function, we evaluate whether a new observation from the target agent follows a normal pattern. In order to construct a reliable anomaly detection method and take into consideration the confidence of the predicted anomaly score, we adopt a Bayesian approach for IRL. The empirical study on publicly available real-world data shows that our proposed method is effective in identifying anomalies.