A Counterfactual Analysis of the Dishonest Casino

The dishonest casino is a well-known hidden Markov model (HMM) used in educational settings to introduce HMMs and graphical models. Here, a sequence of die rolls is observed, with the casino switching between a fair and a loaded die. Typically, the goal is to use the observed rolls to infer the pattern of fair and loaded dice, leading to filtering, smoothing, and Viterbi algorithms. This paper, however, explores how much of the winnings is attributable to the casino's cheating, a counterfactual question beyond the scope of HMM primitives. To address this, we introduce a structural causal model (SCM) consistent with the HMM and show that the expected winnings attributable to cheating (EWAC) can be bounded using linear programs (LPs). Through numerical experiments, we compute these bounds and develop intuition using benchmark SCMs based on independence, comonotonic, and counter-monotonic copulas. We show that tighter bounds are obtained with a time-homogeneity condition on the SCM, while looser bounds allow for an almost explicit LP solution. Domain-specific knowledge like pathwise monotonicity or counterfactual stability can be incorporated via linear constraints. Our work contributes to bounding counterfactuals in causal inference and is the first to develop LP bounds in a dynamic HMM setting, benefiting educational contexts where counterfactual inference is taught.

Model-Free Approximate Bayesian Learning for Large-Scale Conversion Funnel Optimization

The flexibility of choosing the ad action as a function of the consumer state is critical for modern-day marketing campaigns. We study the problem of identifying the optimal sequential personalized interventions that maximize the adoption probability for a new product. We model consumer behavior by a conversion funnel that captures the state of each consumer (e.g., interaction history with the firm) and allows the consumer behavior to vary as a function of both her state and firm's sequential interventions. We show our model captures consumer behavior with very high accuracy (out-of-sample AUC of over 0.95) in a real-world email marketing dataset. However, it results in a very large-scale learning problem, where the firm must learn the state-specific effects of various interventions from consumer interactions. We propose a novel attribution-based decision-making algorithm for this problem that we call model-free approximate Bayesian learning. Our algorithm inherits the interpretability and scalability of Thompson sampling for bandits and maintains an approximate belief over the value of each state-specific intervention. The belief is updated as the algorithm interacts with the consumers. Despite being an approximation to the Bayes update, we prove the asymptotic optimality of our algorithm and analyze its convergence rate. We show that our algorithm significantly outperforms traditional approaches on extensive simulations calibrated to a real-world email marketing dataset.

Counterfactual Analysis in Dynamic Models: Copulas and Bounds

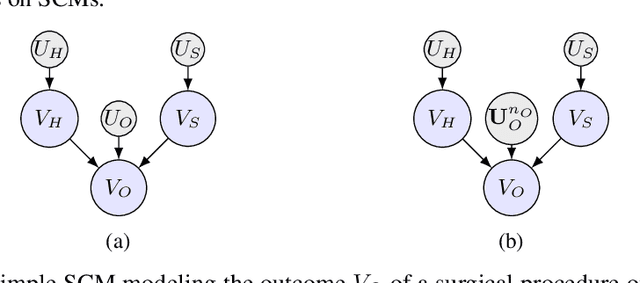
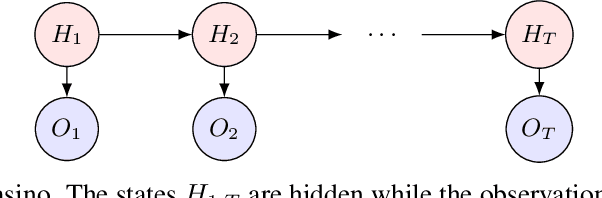
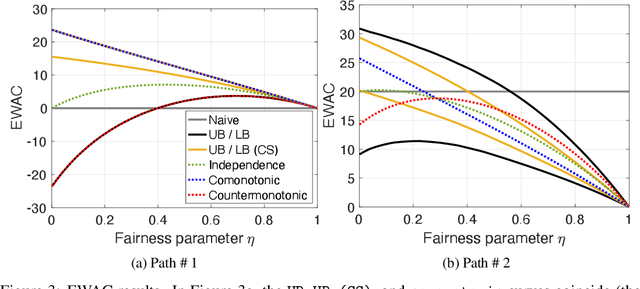
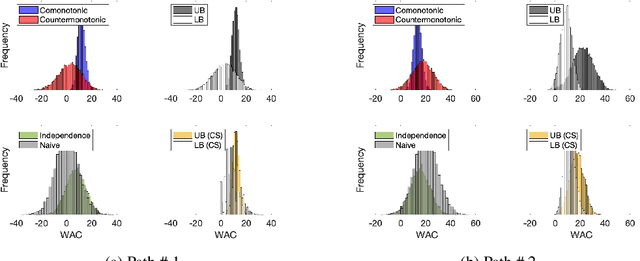
We provide an explicit model of the causal mechanism in a structural causal model (SCM) with the goal of estimating counterfactual quantities of interest (CQIs). We propose some standard dependence structures, i.e. copulas, as base cases for the causal mechanism. While these base cases can be used to construct more interesting copulas, there are uncountably many copulas in general and so we formulate optimization problems for bounding the CQIs. As our ultimate goal is counterfactual reasoning in dynamic models which may have latent-states, we show by way of example that filtering / smoothing / sampling methods for these models can be integrated with our modeling of the causal mechanism. Specifically, we consider the "cheating-at-the-casino" application of a hidden Markov model and use linear programming (LP) to construct lower and upper bounds on the casino's winnings due to cheating. These bounds are considerably tighter when we constrain the copulas in the LPs to be time-independent. We can characterize the entire space of SCMs obeying counterfactual stability (CS), and we use it to negatively answer the open question of Oberst and Sontag [18] regarding the uniqueness of the Gumbel-max mechanism for modeling CS. Our work has applications in epidemiology and legal reasoning, and more generally in counterfactual off-policy evaluation, a topic of increasing interest in the reinforcement learning community.

A Finite Time Analysis of Temporal Difference Learning With Linear Function Approximation

Temporal difference learning (TD) is a simple iterative algorithm used to estimate the value function corresponding to a given policy in a Markov decision process. Although TD is one of the most widely used algorithms in reinforcement learning, its theoretical analysis has proved challenging and few guarantees on its statistical efficiency are available. In this work, we provide a simple and explicit finite time analysis of temporal difference learning with linear function approximation. Except for a few key insights, our analysis mirrors standard techniques for analyzing stochastic gradient descent algorithms, and therefore inherits the simplicity and elegance of that literature. Final sections of the paper show how all of our main results extend to the study of TD learning with eligibility traces, known as TD($\lambda$), and to Q-learning applied in high-dimensional optimal stopping problems.