Counterfactual Analysis in Dynamic Models: Copulas and Bounds
Paper and Code
May 27, 2022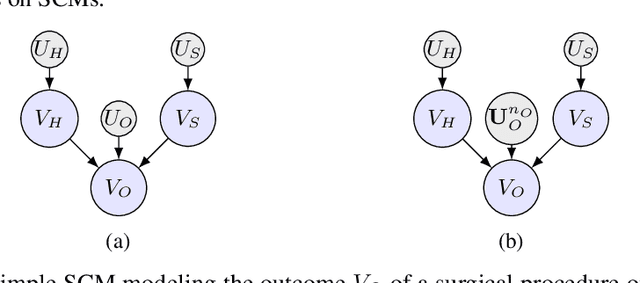
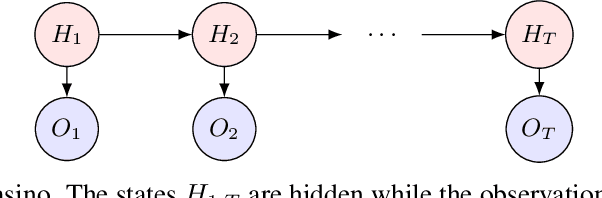
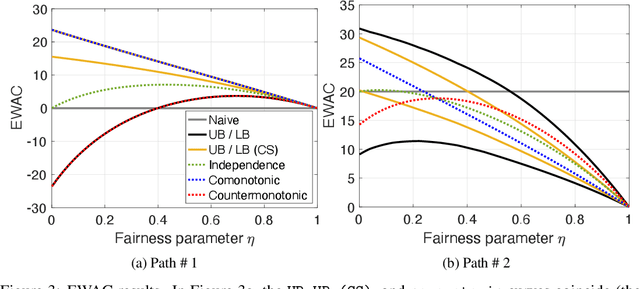
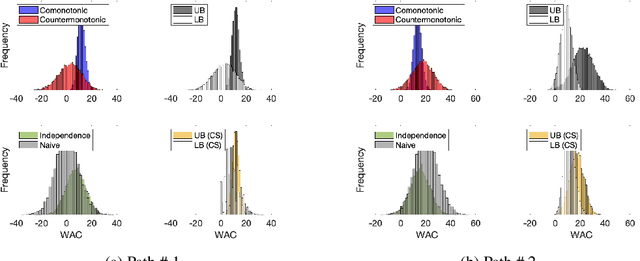
We provide an explicit model of the causal mechanism in a structural causal model (SCM) with the goal of estimating counterfactual quantities of interest (CQIs). We propose some standard dependence structures, i.e. copulas, as base cases for the causal mechanism. While these base cases can be used to construct more interesting copulas, there are uncountably many copulas in general and so we formulate optimization problems for bounding the CQIs. As our ultimate goal is counterfactual reasoning in dynamic models which may have latent-states, we show by way of example that filtering / smoothing / sampling methods for these models can be integrated with our modeling of the causal mechanism. Specifically, we consider the "cheating-at-the-casino" application of a hidden Markov model and use linear programming (LP) to construct lower and upper bounds on the casino's winnings due to cheating. These bounds are considerably tighter when we constrain the copulas in the LPs to be time-independent. We can characterize the entire space of SCMs obeying counterfactual stability (CS), and we use it to negatively answer the open question of Oberst and Sontag [18] regarding the uniqueness of the Gumbel-max mechanism for modeling CS. Our work has applications in epidemiology and legal reasoning, and more generally in counterfactual off-policy evaluation, a topic of increasing interest in the reinforcement learning community.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge