DRO: A Python Library for Distributionally Robust Optimization in Machine Learning

We introduce dro, an open-source Python library for distributionally robust optimization (DRO) for regression and classification problems. The library implements 14 DRO formulations and 9 backbone models, enabling 79 distinct DRO methods. Furthermore, dro is compatible with both scikit-learn and PyTorch. Through vectorization and optimization approximation techniques, dro reduces runtime by 10x to over 1000x compared to baseline implementations on large-scale datasets. Comprehensive documentation is available at https://python-dro.org.

Extreme Conformal Prediction: Reliable Intervals for High-Impact Events

Conformal prediction is a popular method to construct prediction intervals for black-box machine learning models with marginal coverage guarantees. In applications with potentially high-impact events, such as flooding or financial crises, regulators often require very high confidence for such intervals. However, if the desired level of confidence is too large relative to the amount of data used for calibration, then classical conformal methods provide infinitely wide, thus, uninformative prediction intervals. In this paper, we propose a new method to overcome this limitation. We bridge extreme value statistics and conformal prediction to provide reliable and informative prediction intervals with high-confidence coverage, which can be constructed using any black-box extreme quantile regression method. The advantages of this extreme conformal prediction method are illustrated in a simulation study and in an application to flood risk forecasting.

Stochastic Optimization with Optimal Importance Sampling

Importance Sampling (IS) is a widely used variance reduction technique for enhancing the efficiency of Monte Carlo methods, particularly in rare-event simulation and related applications. Despite its power, the performance of IS is often highly sensitive to the choice of the proposal distribution and frequently requires stochastic calibration techniques. While the design and analysis of IS have been extensively studied in estimation settings, applying IS within stochastic optimization introduces a unique challenge: the decision and the IS distribution are mutually dependent, creating a circular optimization structure. This interdependence complicates both the analysis of convergence for decision iterates and the efficiency of the IS scheme. In this paper, we propose an iterative gradient-based algorithm that jointly updates the decision variable and the IS distribution without requiring time-scale separation between the two. Our method achieves the lowest possible asymptotic variance and guarantees global convergence under convexity of the objective and mild assumptions on the IS distribution family. Furthermore, we show that these properties are preserved under linear constraints by incorporating a recent variant of Nesterov's dual averaging method.

Prediction-Enhanced Monte Carlo: A Machine Learning View on Control Variate

Despite being an essential tool across engineering and finance, Monte Carlo simulation can be computationally intensive, especially in large-scale, path-dependent problems that hinder straightforward parallelization. A natural alternative is to replace simulation with machine learning or surrogate prediction, though this introduces challenges in understanding the resulting errors.We introduce a Prediction-Enhanced Monte Carlo (PEMC) framework where we leverage machine learning prediction as control variates, thus maintaining unbiased evaluations instead of the direct use of ML predictors. Traditional control variate methods require knowledge of means and focus on per-sample variance reduction. In contrast, PEMC aims at overall cost-aware variance reduction, eliminating the need for mean knowledge. PEMC leverages pre-trained neural architectures to construct effective control variates and replaces computationally expensive sample-path generation with efficient neural network evaluations. This allows PEMC to address scenarios where no good control variates are known. We showcase the efficacy of PEMC through two production-grade exotic option-pricing problems: swaption pricing in HJM model and the variance swap pricing in a stochastic local volatility model.

LLM Embeddings Improve Test-time Adaptation to Tabular $Y|X$-Shifts

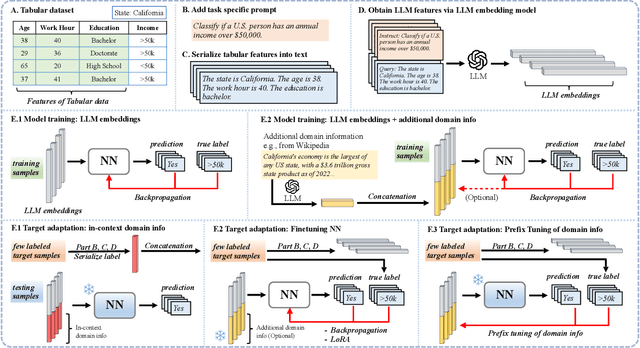
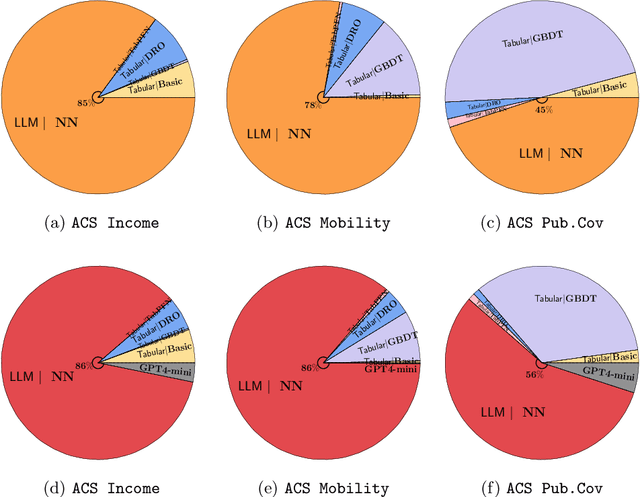
For tabular datasets, the change in the relationship between the label and covariates ($Y|X$-shifts) is common due to missing variables (a.k.a. confounders). Since it is impossible to generalize to a completely new and unknown domain, we study models that are easy to adapt to the target domain even with few labeled examples. We focus on building more informative representations of tabular data that can mitigate $Y|X$-shifts, and propose to leverage the prior world knowledge in LLMs by serializing (write down) the tabular data to encode it. We find LLM embeddings alone provide inconsistent improvements in robustness, but models trained on them can be well adapted/finetuned to the target domain even using 32 labeled observations. Our finding is based on a comprehensive and systematic study consisting of 7650 source-target pairs and benchmark against 261,000 model configurations trained by 22 algorithms. Our observation holds when ablating the size of accessible target data and different adaptation strategies. The code is available at https://github.com/namkoong-lab/LLM-Tabular-Shifts.

Bayesian Bandit Algorithms with Approximate Inference in Stochastic Linear Bandits

Bayesian bandit algorithms with approximate Bayesian inference have been widely used in real-world applications. Nevertheless, their theoretical justification is less investigated in the literature, especially for contextual bandit problems. To fill this gap, we propose a general theoretical framework to analyze stochastic linear bandits in the presence of approximate inference and conduct regret analysis on two Bayesian bandit algorithms, Linear Thompson sampling (LinTS) and the extension of Bayesian Upper Confidence Bound, namely Linear Bayesian Upper Confidence Bound (LinBUCB). We demonstrate that both LinTS and LinBUCB can preserve their original rates of regret upper bound but with a sacrifice of larger constant terms when applied with approximate inference. These results hold for general Bayesian inference approaches, under the assumption that the inference error measured by two different $\alpha$-divergences is bounded. Additionally, by introducing a new definition of well-behaved distributions, we show that LinBUCB improves the regret rate of LinTS from $\tilde{O}(d^{3/2}\sqrt{T})$ to $\tilde{O}(d\sqrt{T})$, matching the minimax optimal rate. To our knowledge, this work provides the first regret bounds in the setting of stochastic linear bandits with bounded approximate inference errors.

Mallows-DPO: Fine-Tune Your LLM with Preference Dispersions

Direct Preference Optimization (DPO) has recently emerged as a popular approach to improve reinforcement learning with human feedback (RLHF), leading to better techniques to fine-tune large language models (LLM). A weakness of DPO, however, lies in its lack of capability to characterize the diversity of human preferences. Inspired by Mallows' theory of preference ranking, we develop in this paper a new approach, the Mallows-DPO. A distinct feature of this approach is a dispersion index, which reflects the dispersion of human preference to prompts. We show that existing DPO models can be reduced to special cases of this dispersion index, thus unified with Mallows-DPO. More importantly, we demonstrate (empirically) how to use this dispersion index to enhance the performance of DPO in a broad array of benchmark tasks, from synthetic bandit selection to controllable generations and dialogues, while maintaining great generalization capabilities.

Bagging Improves Generalization Exponentially

Bagging is a popular ensemble technique to improve the accuracy of machine learning models. It hinges on the well-established rationale that, by repeatedly retraining on resampled data, the aggregated model exhibits lower variance and hence higher stability, especially for discontinuous base learners. In this paper, we provide a new perspective on bagging: By suitably aggregating the base learners at the parametrization instead of the output level, bagging improves generalization performances exponentially, a strength that is significantly more powerful than variance reduction. More precisely, we show that for general stochastic optimization problems that suffer from slowly (i.e., polynomially) decaying generalization errors, bagging can effectively reduce these errors to an exponential decay. Moreover, this power of bagging is agnostic to the solution schemes, including common empirical risk minimization, distributionally robust optimization, and various regularizations. We demonstrate how bagging can substantially improve generalization performances in a range of examples involving heavy-tailed data that suffer from intrinsically slow rates.

Learning from Sparse Offline Datasets via Conservative Density Estimation

Offline reinforcement learning (RL) offers a promising direction for learning policies from pre-collected datasets without requiring further interactions with the environment. However, existing methods struggle to handle out-of-distribution (OOD) extrapolation errors, especially in sparse reward or scarce data settings. In this paper, we propose a novel training algorithm called Conservative Density Estimation (CDE), which addresses this challenge by explicitly imposing constraints on the state-action occupancy stationary distribution. CDE overcomes the limitations of existing approaches, such as the stationary distribution correction method, by addressing the support mismatch issue in marginal importance sampling. Our method achieves state-of-the-art performance on the D4RL benchmark. Notably, CDE consistently outperforms baselines in challenging tasks with sparse rewards or insufficient data, demonstrating the advantages of our approach in addressing the extrapolation error problem in offline RL.

Resampling Stochastic Gradient Descent Cheaply for Efficient Uncertainty Quantification

Stochastic gradient descent (SGD) or stochastic approximation has been widely used in model training and stochastic optimization. While there is a huge literature on analyzing its convergence, inference on the obtained solutions from SGD has only been recently studied, yet is important due to the growing need for uncertainty quantification. We investigate two computationally cheap resampling-based methods to construct confidence intervals for SGD solutions. One uses multiple, but few, SGDs in parallel via resampling with replacement from the data, and another operates this in an online fashion. Our methods can be regarded as enhancements of established bootstrap schemes to substantially reduce the computation effort in terms of resampling requirements, while at the same time bypassing the intricate mixing conditions in existing batching methods. We achieve these via a recent so-called cheap bootstrap idea and Berry-Esseen-type bound for SGD.