Prediction-Enhanced Monte Carlo: A Machine Learning View on Control Variate

Despite being an essential tool across engineering and finance, Monte Carlo simulation can be computationally intensive, especially in large-scale, path-dependent problems that hinder straightforward parallelization. A natural alternative is to replace simulation with machine learning or surrogate prediction, though this introduces challenges in understanding the resulting errors.We introduce a Prediction-Enhanced Monte Carlo (PEMC) framework where we leverage machine learning prediction as control variates, thus maintaining unbiased evaluations instead of the direct use of ML predictors. Traditional control variate methods require knowledge of means and focus on per-sample variance reduction. In contrast, PEMC aims at overall cost-aware variance reduction, eliminating the need for mean knowledge. PEMC leverages pre-trained neural architectures to construct effective control variates and replaces computationally expensive sample-path generation with efficient neural network evaluations. This allows PEMC to address scenarios where no good control variates are known. We showcase the efficacy of PEMC through two production-grade exotic option-pricing problems: swaption pricing in HJM model and the variance swap pricing in a stochastic local volatility model.

Deep Learning-based Approaches for State Space Models: A Selective Review

State-space models (SSMs) offer a powerful framework for dynamical system analysis, wherein the temporal dynamics of the system are assumed to be captured through the evolution of the latent states, which govern the values of the observations. This paper provides a selective review of recent advancements in deep neural network-based approaches for SSMs, and presents a unified perspective for discrete time deep state space models and continuous time ones such as latent neural Ordinary Differential and Stochastic Differential Equations. It starts with an overview of the classical maximum likelihood based approach for learning SSMs, reviews variational autoencoder as a general learning pipeline for neural network-based approaches in the presence of latent variables, and discusses in detail representative deep learning models that fall under the SSM framework. Very recent developments, where SSMs are used as standalone architectural modules for improving efficiency in sequence modeling, are also examined. Finally, examples involving mixed frequency and irregularly-spaced time series data are presented to demonstrate the advantage of SSMs in these settings.

A VAE-based Framework for Learning Multi-Level Neural Granger-Causal Connectivity

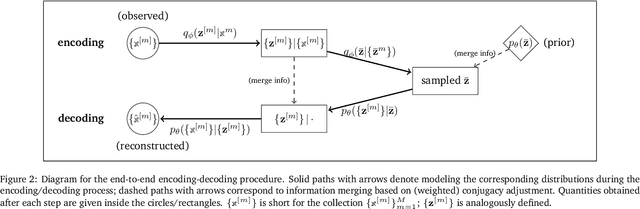
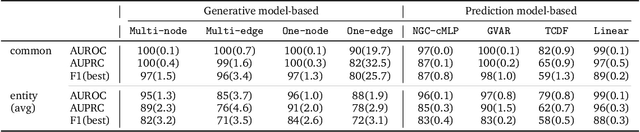
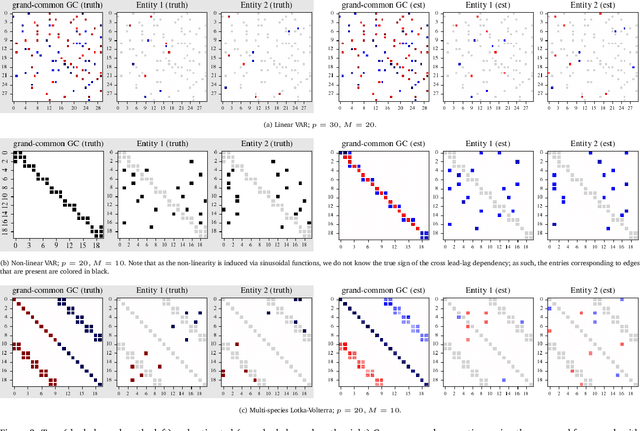
Granger causality has been widely used in various application domains to capture lead-lag relationships amongst the components of complex dynamical systems, and the focus in extant literature has been on a single dynamical system. In certain applications in macroeconomics and neuroscience, one has access to data from a collection of related such systems, wherein the modeling task of interest is to extract the shared common structure that is embedded across them, as well as to identify the idiosyncrasies within individual ones. This paper introduces a Variational Autoencoder (VAE) based framework that jointly learns Granger-causal relationships amongst components in a collection of related-yet-heterogeneous dynamical systems, and handles the aforementioned task in a principled way. The performance of the proposed framework is evaluated on several synthetic data settings and benchmarked against existing approaches designed for individual system learning. The method is further illustrated on a real dataset involving time series data from a neurophysiological experiment and produces interpretable results.