Haoxian Chen
VMonarch: Efficient Video Diffusion Transformers with Structured Attention
Jan 29, 2026Abstract:The quadratic complexity of the attention mechanism severely limits the context scalability of Video Diffusion Transformers (DiTs). We find that the highly sparse spatio-temporal attention patterns exhibited in Video DiTs can be naturally represented by the Monarch matrix. It is a class of structured matrices with flexible sparsity, enabling sub-quadratic attention via an alternating minimization algorithm. Accordingly, we propose VMonarch, a novel attention mechanism for Video DiTs that enables efficient computation over the dynamic sparse patterns with structured Monarch matrices. First, we adapt spatio-temporal Monarch factorization to explicitly capture the intra-frame and inter-frame correlations of the video data. Second, we introduce a recomputation strategy to mitigate artifacts arising from instabilities during alternating minimization of Monarch matrices. Third, we propose a novel online entropy algorithm fused into FlashAttention, enabling fast Monarch matrix updates for long sequences. Extensive experiments demonstrate that VMonarch achieves comparable or superior generation quality to full attention on VBench after minimal tuning. It overcomes the attention bottleneck in Video DiTs, reduces attention FLOPs by a factor of 17.5, and achieves a speedup of over 5x in attention computation for long videos, surpassing state-of-the-art sparse attention methods at 90% sparsity.
Token-Level Uncertainty Estimation for Large Language Model Reasoning
May 16, 2025Abstract:While Large Language Models (LLMs) have demonstrated impressive capabilities, their output quality remains inconsistent across various application scenarios, making it difficult to identify trustworthy responses, especially in complex tasks requiring multi-step reasoning. In this paper, we propose a token-level uncertainty estimation framework to enable LLMs to self-assess and self-improve their generation quality in mathematical reasoning. Specifically, we introduce low-rank random weight perturbation to LLM decoding, generating predictive distributions that we use to estimate token-level uncertainties. We then aggregate these uncertainties to reflect semantic uncertainty of the generated sequences. Experiments on mathematical reasoning datasets of varying difficulty demonstrate that our token-level uncertainty metrics strongly correlate with answer correctness and model robustness. Additionally, we explore using uncertainty to directly enhance the model's reasoning performance through multiple generations and the particle filtering algorithm. Our approach consistently outperforms existing uncertainty estimation methods, establishing effective uncertainty estimation as a valuable tool for both evaluating and improving reasoning generation in LLMs.
Fine-Tuning Diffusion Generative Models via Rich Preference Optimization
Mar 13, 2025
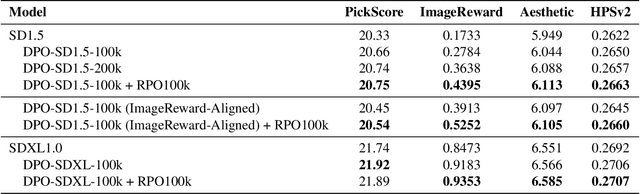
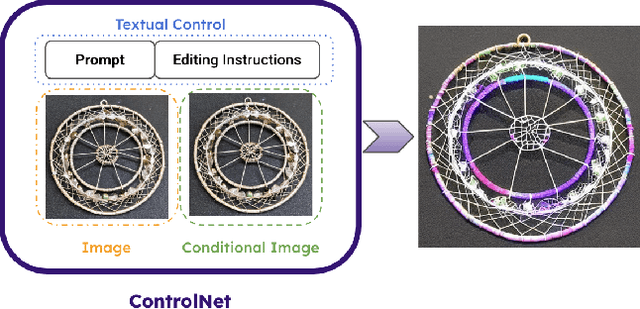
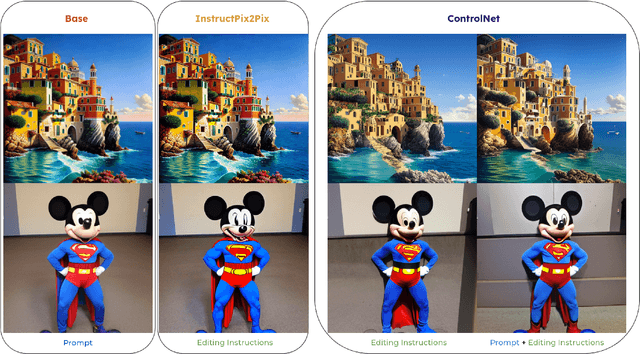
Abstract:We introduce Rich Preference Optimization (RPO), a novel pipeline that leverages rich feedback signals to improve the curation of preference pairs for fine-tuning text-to-image diffusion models. Traditional methods, like Diffusion-DPO, often rely solely on reward model labeling, which can be opaque, offer limited insights into the rationale behind preferences, and are prone to issues such as reward hacking or overfitting. In contrast, our approach begins with generating detailed critiques of synthesized images to extract reliable and actionable image editing instructions. By implementing these instructions, we create refined images, resulting in synthetic, informative preference pairs that serve as enhanced tuning datasets. We demonstrate the effectiveness of our pipeline and the resulting datasets in fine-tuning state-of-the-art diffusion models.
Score as Action: Fine-Tuning Diffusion Generative Models by Continuous-time Reinforcement Learning
Feb 03, 2025



Abstract:Reinforcement learning from human feedback (RLHF), which aligns a diffusion model with input prompt, has become a crucial step in building reliable generative AI models. Most works in this area use a discrete-time formulation, which is prone to induced errors, and often not applicable to models with higher-order/black-box solvers. The objective of this study is to develop a disciplined approach to fine-tune diffusion models using continuous-time RL, formulated as a stochastic control problem with a reward function that aligns the end result (terminal state) with input prompt. The key idea is to treat score matching as controls or actions, and thereby making connections to policy optimization and regularization in continuous-time RL. To carry out this idea, we lay out a new policy optimization framework for continuous-time RL, and illustrate its potential in enhancing the value networks design space via leveraging the structural property of diffusion models. We validate the advantages of our method by experiments in downstream tasks of fine-tuning large-scale Text2Image models of Stable Diffusion v1.5.
Prediction-Enhanced Monte Carlo: A Machine Learning View on Control Variate
Dec 15, 2024



Abstract:Despite being an essential tool across engineering and finance, Monte Carlo simulation can be computationally intensive, especially in large-scale, path-dependent problems that hinder straightforward parallelization. A natural alternative is to replace simulation with machine learning or surrogate prediction, though this introduces challenges in understanding the resulting errors.We introduce a Prediction-Enhanced Monte Carlo (PEMC) framework where we leverage machine learning prediction as control variates, thus maintaining unbiased evaluations instead of the direct use of ML predictors. Traditional control variate methods require knowledge of means and focus on per-sample variance reduction. In contrast, PEMC aims at overall cost-aware variance reduction, eliminating the need for mean knowledge. PEMC leverages pre-trained neural architectures to construct effective control variates and replaces computationally expensive sample-path generation with efficient neural network evaluations. This allows PEMC to address scenarios where no good control variates are known. We showcase the efficacy of PEMC through two production-grade exotic option-pricing problems: swaption pricing in HJM model and the variance swap pricing in a stochastic local volatility model.
Scores as Actions: a framework of fine-tuning diffusion models by continuous-time reinforcement learning
Sep 12, 2024Abstract:Reinforcement Learning from human feedback (RLHF) has been shown a promising direction for aligning generative models with human intent and has also been explored in recent works for alignment of diffusion generative models. In this work, we provide a rigorous treatment by formulating the task of fine-tuning diffusion models, with reward functions learned from human feedback, as an exploratory continuous-time stochastic control problem. Our key idea lies in treating the score-matching functions as controls/actions, and upon this, we develop a unified framework from a continuous-time perspective, to employ reinforcement learning (RL) algorithms in terms of improving the generation quality of diffusion models. We also develop the corresponding continuous-time RL theory for policy optimization and regularization under assumptions of stochastic different equations driven environment. Experiments on the text-to-image (T2I) generation will be reported in the accompanied paper.
Mallows-DPO: Fine-Tune Your LLM with Preference Dispersions
May 23, 2024



Abstract:Direct Preference Optimization (DPO) has recently emerged as a popular approach to improve reinforcement learning with human feedback (RLHF), leading to better techniques to fine-tune large language models (LLM). A weakness of DPO, however, lies in its lack of capability to characterize the diversity of human preferences. Inspired by Mallows' theory of preference ranking, we develop in this paper a new approach, the Mallows-DPO. A distinct feature of this approach is a dispersion index, which reflects the dispersion of human preference to prompts. We show that existing DPO models can be reduced to special cases of this dispersion index, thus unified with Mallows-DPO. More importantly, we demonstrate (empirically) how to use this dispersion index to enhance the performance of DPO in a broad array of benchmark tasks, from synthetic bandit selection to controllable generations and dialogues, while maintaining great generalization capabilities.
Pseudo-Bayesian Optimization
Oct 15, 2023Abstract:Bayesian Optimization is a popular approach for optimizing expensive black-box functions. Its key idea is to use a surrogate model to approximate the objective and, importantly, quantify the associated uncertainty that allows a sequential search of query points that balance exploitation-exploration. Gaussian process (GP) has been a primary candidate for the surrogate model, thanks to its Bayesian-principled uncertainty quantification power and modeling flexibility. However, its challenges have also spurred an array of alternatives whose convergence properties could be more opaque. Motivated by these, we study in this paper an axiomatic framework that elicits the minimal requirements to guarantee black-box optimization convergence that could apply beyond GP-related methods. Moreover, we leverage the design freedom in our framework, which we call Pseudo-Bayesian Optimization, to construct empirically superior algorithms. In particular, we show how using simple local regression, and a suitable "randomized prior" construction to quantify uncertainty, not only guarantees convergence but also consistently outperforms state-of-the-art benchmarks in examples ranging from high-dimensional synthetic experiments to realistic hyperparameter tuning and robotic applications.
Hybrid Random Features
Oct 13, 2021
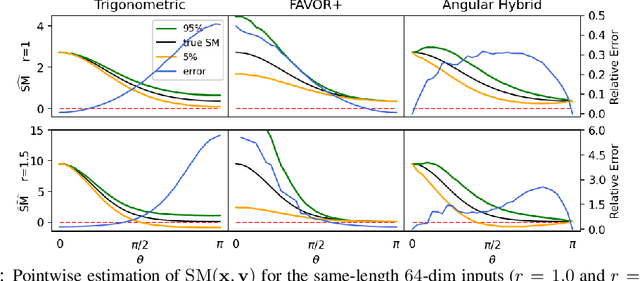
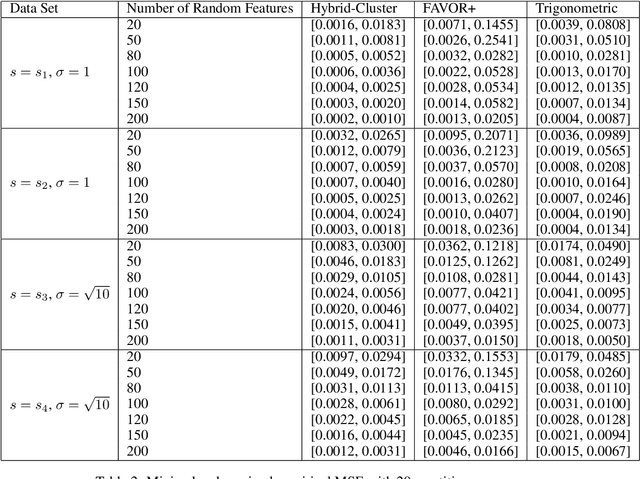
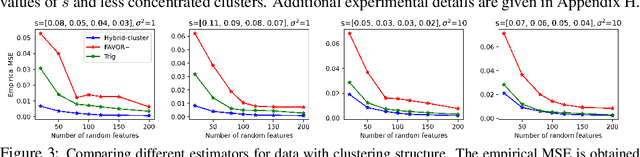
Abstract:We propose a new class of random feature methods for linearizing softmax and Gaussian kernels called hybrid random features (HRFs) that automatically adapt the quality of kernel estimation to provide most accurate approximation in the defined regions of interest. Special instantiations of HRFs lead to well-known methods such as trigonometric (Rahimi and Recht, 2007) or (recently introduced in the context of linear-attention Transformers) positive random features (Choromanski et al., 2021). By generalizing Bochner's Theorem for softmax/Gaussian kernels and leveraging random features for compositional kernels, the HRF-mechanism provides strong theoretical guarantees - unbiased approximation and strictly smaller worst-case relative errors than its counterparts. We conduct exhaustive empirical evaluation of HRF ranging from pointwise kernel estimation experiments, through tests on data admitting clustering structure to benchmarking implicit-attention Transformers (also for downstream Robotics applications), demonstrating its quality in a wide spectrum of machine learning problems.
Graph Kernel Attention Transformers
Jul 16, 2021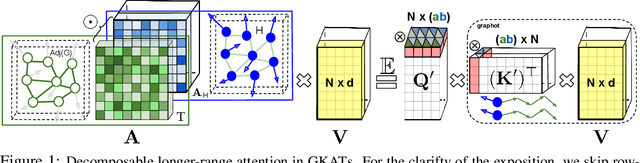
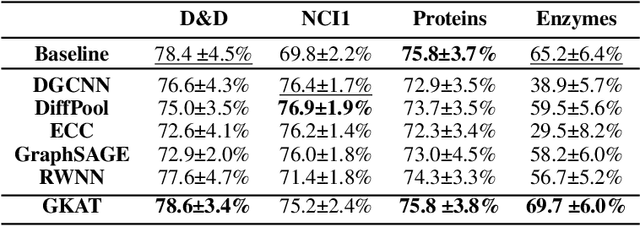
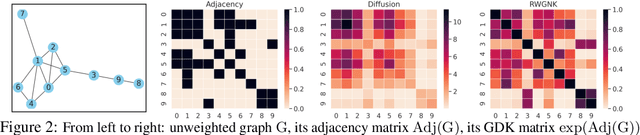

Abstract:We introduce a new class of graph neural networks (GNNs), by combining several concepts that were so far studied independently - graph kernels, attention-based networks with structural priors and more recently, efficient Transformers architectures applying small memory footprint implicit attention methods via low rank decomposition techniques. The goal of the paper is twofold. Proposed by us Graph Kernel Attention Transformers (or GKATs) are much more expressive than SOTA GNNs as capable of modeling longer-range dependencies within a single layer. Consequently, they can use more shallow architecture design. Furthermore, GKAT attention layers scale linearly rather than quadratically in the number of nodes of the input graphs, even when those graphs are dense, requiring less compute than their regular graph attention counterparts. They achieve it by applying new classes of graph kernels admitting random feature map decomposition via random walks on graphs. As a byproduct of the introduced techniques, we obtain a new class of learnable graph sketches, called graphots, compactly encoding topological graph properties as well as nodes' features. We conducted exhaustive empirical comparison of our method with nine different GNN classes on tasks ranging from motif detection through social network classification to bioinformatics challenges, showing consistent gains coming from GKATs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge