UniGen: Unified Modeling of Initial Agent States and Trajectories for Generating Autonomous Driving Scenarios

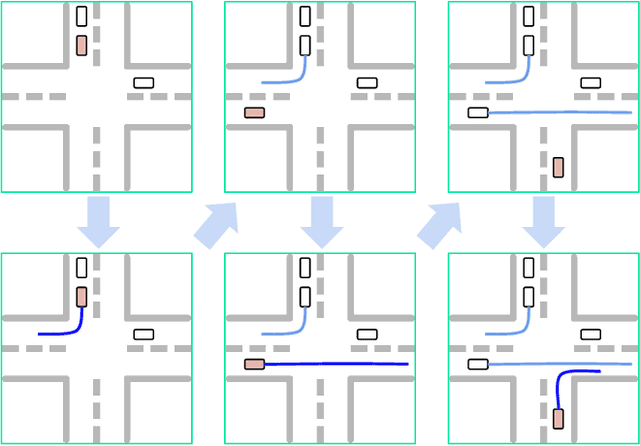
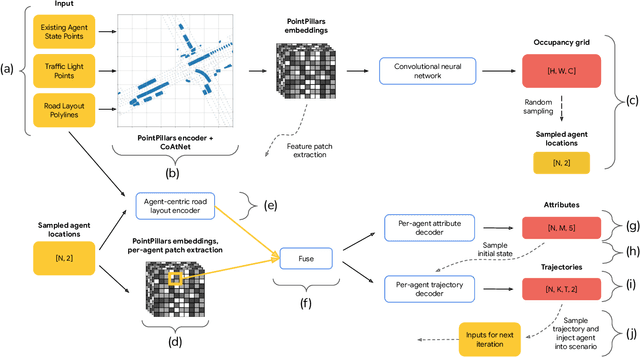
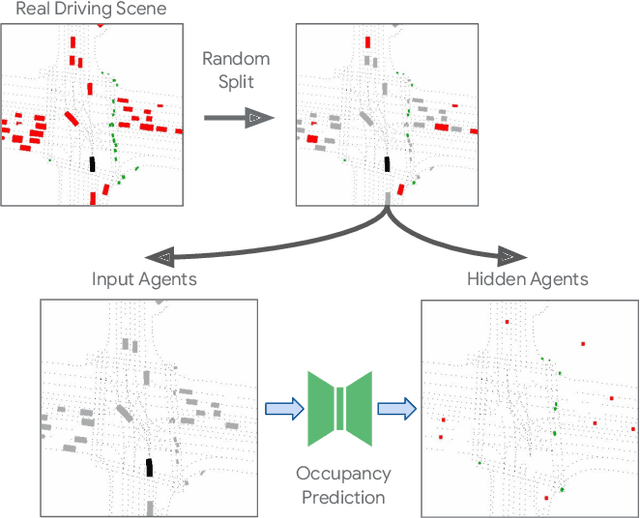
This paper introduces UniGen, a novel approach to generating new traffic scenarios for evaluating and improving autonomous driving software through simulation. Our approach models all driving scenario elements in a unified model: the position of new agents, their initial state, and their future motion trajectories. By predicting the distributions of all these variables from a shared global scenario embedding, we ensure that the final generated scenario is fully conditioned on all available context in the existing scene. Our unified modeling approach, combined with autoregressive agent injection, conditions the placement and motion trajectory of every new agent on all existing agents and their trajectories, leading to realistic scenarios with low collision rates. Our experimental results show that UniGen outperforms prior state of the art on the Waymo Open Motion Dataset.

Scalable Neural Network Kernels

We introduce the concept of scalable neural network kernels (SNNKs), the replacements of regular feedforward layers (FFLs), capable of approximating the latter, but with favorable computational properties. SNNKs effectively disentangle the inputs from the parameters of the neural network in the FFL, only to connect them in the final computation via the dot-product kernel. They are also strictly more expressive, as allowing to model complicated relationships beyond the functions of the dot-products of parameter-input vectors. We also introduce the neural network bundling process that applies SNNKs to compactify deep neural network architectures, resulting in additional compression gains. In its extreme version, it leads to the fully bundled network whose optimal parameters can be expressed via explicit formulae for several loss functions (e.g. mean squared error), opening a possibility to bypass backpropagation. As a by-product of our analysis, we introduce the mechanism of the universal random features (or URFs), applied to instantiate several SNNK variants, and interesting on its own in the context of scalable kernel methods. We provide rigorous theoretical analysis of all these concepts as well as an extensive empirical evaluation, ranging from point-wise kernel estimation to Transformers' fine-tuning with novel adapter layers inspired by SNNKs. Our mechanism provides up to 5x reduction in the number of trainable parameters, while maintaining competitive accuracy.

Efficient Graph Field Integrators Meet Point Clouds

We present two new classes of algorithms for efficient field integration on graphs encoding point clouds. The first class, SeparatorFactorization(SF), leverages the bounded genus of point cloud mesh graphs, while the second class, RFDiffusion(RFD), uses popular epsilon-nearest-neighbor graph representations for point clouds. Both can be viewed as providing the functionality of Fast Multipole Methods (FMMs), which have had a tremendous impact on efficient integration, but for non-Euclidean spaces. We focus on geometries induced by distributions of walk lengths between points (e.g., shortest-path distance). We provide an extensive theoretical analysis of our algorithms, obtaining new results in structural graph theory as a byproduct. We also perform exhaustive empirical evaluation, including on-surface interpolation for rigid and deformable objects (particularly for mesh-dynamics modeling), Wasserstein distance computations for point clouds, and the Gromov-Wasserstein variant.

Learning a Fourier Transform for Linear Relative Positional Encodings in Transformers

We propose a new class of linear Transformers called FourierLearner-Transformers (FLTs), which incorporate a wide range of relative positional encoding mechanisms (RPEs). These include regular RPE techniques applied for nongeometric data, as well as novel RPEs operating on the sequences of tokens embedded in higher-dimensional Euclidean spaces (e.g. point clouds). FLTs construct the optimal RPE mechanism implicitly by learning its spectral representation. As opposed to other architectures combining efficient low-rank linear attention with RPEs, FLTs remain practical in terms of their memory usage and do not require additional assumptions about the structure of the RPE-mask. FLTs allow also for applying certain structural inductive bias techniques to specify masking strategies, e.g. they provide a way to learn the so-called local RPEs introduced in this paper and providing accuracy gains as compared with several other linear Transformers for language modeling. We also thoroughly tested FLTs on other data modalities and tasks, such as: image classification and 3D molecular modeling. For 3D-data FLTs are, to the best of our knowledge, the first Transformers architectures providing RPE-enhanced linear attention.

FAVOR#: Sharp Attention Kernel Approximations via New Classes of Positive Random Features

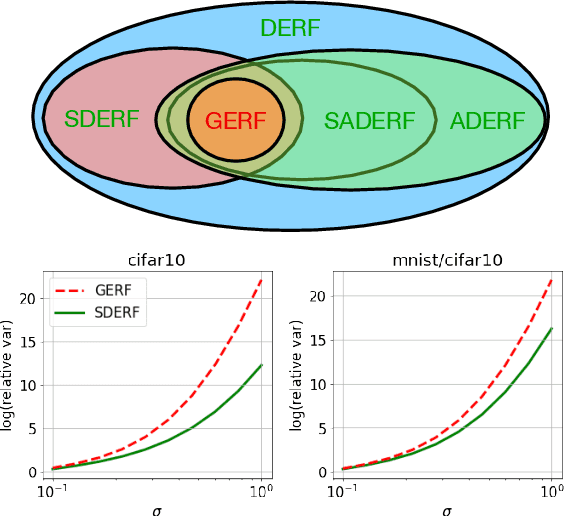
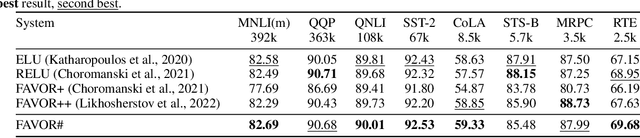
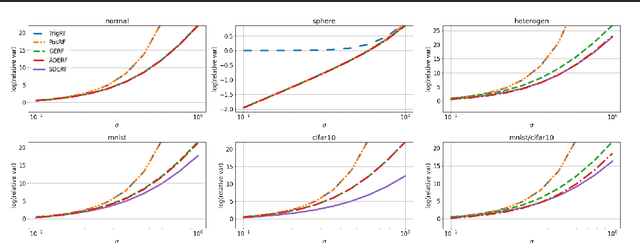
The problem of efficient approximation of a linear operator induced by the Gaussian or softmax kernel is often addressed using random features (RFs) which yield an unbiased approximation of the operator's result. Such operators emerge in important applications ranging from kernel methods to efficient Transformers. We propose parameterized, positive, non-trigonometric RFs which approximate Gaussian and softmax-kernels. In contrast to traditional RF approximations, parameters of these new methods can be optimized to reduce the variance of the approximation, and the optimum can be expressed in closed form. We show that our methods lead to variance reduction in practice ($e^{10}$-times smaller variance and beyond) and outperform previous methods in a kernel regression task. Using our proposed mechanism, we also present FAVOR#, a method for self-attention approximation in Transformers. We show that FAVOR# outperforms other random feature methods in speech modelling and natural language processing.

Simplex Random Features

We present Simplex Random Features (SimRFs), a new random feature (RF) mechanism for unbiased approximation of the softmax and Gaussian kernels by geometrical correlation of random projection vectors. We prove that SimRFs provide the smallest possible mean square error (MSE) on unbiased estimates of these kernels among the class of weight-independent geometrically-coupled positive random feature (PRF) mechanisms, substantially outperforming the previously most accurate Orthogonal Random Features at no observable extra cost. We present a more computationally expensive SimRFs+ variant, which we prove is asymptotically optimal in the broader family of weight-dependent geometrical coupling schemes (which permit correlations between random vector directions and norms). In extensive empirical studies, we show consistent gains provided by SimRFs in settings including pointwise kernel estimation, nonparametric classification and scalable Transformers.

Adaptive Computation with Elastic Input Sequence

When solving a problem, human beings have the adaptive ability in terms of the type of information they use, the procedure they take, and the amount of time they spend approaching and solving the problem. However, most standard neural networks have the same function type and fixed computation budget on different samples regardless of their nature and difficulty. Adaptivity is a powerful paradigm as it not only imbues practitioners with flexibility pertaining to the downstream usage of these models but can also serve as a powerful inductive bias for solving certain challenging classes of problems. In this work, we propose a new strategy, AdaTape, that enables dynamic computation in neural networks via adaptive tape tokens. AdaTape employs an elastic input sequence by equipping an existing architecture with a dynamic read-and-write tape. Specifically, we adaptively generate input sequences using tape tokens obtained from a tape bank that can either be trainable or generated from input data. We analyze the challenges and requirements to obtain dynamic sequence content and length, and propose the Adaptive Tape Reader (ATR) algorithm to achieve both objectives. Via extensive experiments on image recognition tasks, we show that AdaTape can achieve better performance while maintaining the computational cost.

Automated Deep Aberration Detection from Chromosome Karyotype Images

Chromosome analysis is essential for diagnosing genetic disorders. For hematologic malignancies, identification of somatic clonal aberrations by karyotype analysis remains the standard of care. However, karyotyping is costly and time-consuming because of the largely manual process and the expertise required in identifying and annotating aberrations. Efforts to automate karyotype analysis to date fell short in aberration detection. Using a training set of ~10k patient specimens and ~50k karyograms from over 5 years from the Fred Hutchinson Cancer Center, we created a labeled set of images representing individual chromosomes. These individual chromosomes were used to train and assess deep learning models for classifying the 24 human chromosomes and identifying chromosomal aberrations. The top-accuracy models utilized the recently introduced Topological Vision Transformers (TopViTs) with 2-level-block-Toeplitz masking, to incorporate structural inductive bias. TopViT outperformed CNN (Inception) models with >99.3% accuracy for chromosome identification, and exhibited accuracies >99% for aberration detection in most aberrations. Notably, we were able to show high-quality performance even in "few shot" learning scenarios. Incorporating the definition of clonality substantially improved both precision and recall (sensitivity). When applied to "zero shot" scenarios, the model captured aberrations without training, with perfect precision at >50% recall. Together these results show that modern deep learning models can approach expert-level performance for chromosome aberration detection. To our knowledge, this is the first study demonstrating the downstream effectiveness of TopViTs. These results open up exciting opportunities for not only expediting patient results but providing a scalable technology for early screening of low-abundance chromosomal lesions.

Chefs' Random Tables: Non-Trigonometric Random Features

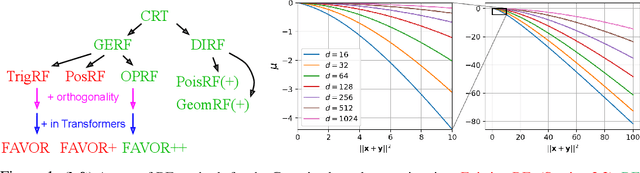
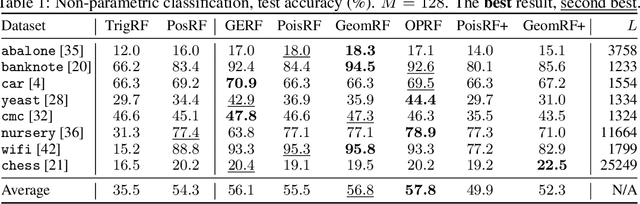
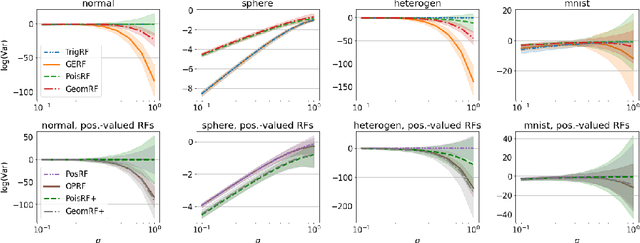
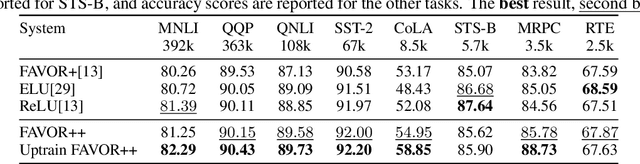
We introduce chefs' random tables (CRTs), a new class of non-trigonometric random features (RFs) to approximate Gaussian and softmax kernels. CRTs are an alternative to standard random kitchen sink (RKS) methods, which inherently rely on the trigonometric maps. We present variants of CRTs where RFs are positive, a key requirement for applications in recent low-rank Transformers. Further variance reduction is possible by leveraging statistics which are simple to compute. One instantiation of CRTs, the optimal positive random features (OPRFs), is to our knowledge the first RF method for unbiased softmax kernel estimation with positive and bounded RFs, resulting in exponentially small tails and much lower variance than its counterparts. As we show, orthogonal random features applied in OPRFs provide additional variance reduction for any dimensionality $d$ (not only asymptotically for sufficiently large $d$, as for RKS). We test CRTs on many tasks ranging from non-parametric classification to training Transformers for text, speech and image data, obtaining new state-of-the-art results for low-rank text Transformers, while providing linear space and time complexity.

PolyViT: Co-training Vision Transformers on Images, Videos and Audio

Can we train a single transformer model capable of processing multiple modalities and datasets, whilst sharing almost all of its learnable parameters? We present PolyViT, a model trained on image, audio and video which answers this question. By co-training different tasks on a single modality, we are able to improve the accuracy of each individual task and achieve state-of-the-art results on 5 standard video- and audio-classification datasets. Co-training PolyViT on multiple modalities and tasks leads to a model that is even more parameter-efficient, and learns representations that generalize across multiple domains. Moreover, we show that co-training is simple and practical to implement, as we do not need to tune hyperparameters for each combination of datasets, but can simply adapt those from standard, single-task training.