Optimal Time Complexity Algorithms for Computing General Random Walk Graph Kernels on Sparse Graphs

We present the first linear time complexity randomized algorithms for unbiased approximation of the celebrated family of general random walk kernels (RWKs) for sparse graphs. This includes both labelled and unlabelled instances. The previous fastest methods for general RWKs were of cubic time complexity and not applicable to labelled graphs. Our method samples dependent random walks to compute novel graph embeddings in $\mathbb{R}^d$ whose dot product is equal to the true RWK in expectation. It does so without instantiating the direct product graph in memory, meaning we can scale to massive datasets that cannot be stored on a single machine. We derive exponential concentration bounds to prove that our estimator is sharp, and show that the ability to approximate general RWKs (rather than just special cases) unlocks efficient implicit graph kernel learning. Our method is up to $\mathbf{27\times}$ faster than its counterparts for efficient computation on large graphs and scales to graphs $\mathbf{128 \times}$ bigger than largest examples amenable to brute-force computation.

Linear Transformer Topological Masking with Graph Random Features

When training transformers on graph-structured data, incorporating information about the underlying topology is crucial for good performance. Topological masking, a type of relative position encoding, achieves this by upweighting or downweighting attention depending on the relationship between the query and keys in a graph. In this paper, we propose to parameterise topological masks as a learnable function of a weighted adjacency matrix -- a novel, flexible approach which incorporates a strong structural inductive bias. By approximating this mask with graph random features (for which we prove the first known concentration bounds), we show how this can be made fully compatible with linear attention, preserving $\mathcal{O}(N)$ time and space complexity with respect to the number of input tokens. The fastest previous alternative was $\mathcal{O}(N \log N)$ and only suitable for specific graphs. Our efficient masking algorithms provide strong performance gains for tasks on image and point cloud data, including with $>30$k nodes.

Variance-Reducing Couplings for Random Features: Perspectives from Optimal Transport

Random features (RFs) are a popular technique to scale up kernel methods in machine learning, replacing exact kernel evaluations with stochastic Monte Carlo estimates. They underpin models as diverse as efficient transformers (by approximating attention) to sparse spectrum Gaussian processes (by approximating the covariance function). Efficiency can be further improved by speeding up the convergence of these estimates: a variance reduction problem. We tackle this through the unifying framework of optimal transport, using theoretical insights and numerical algorithms to develop novel, high-performing RF couplings for kernels defined on Euclidean and discrete input spaces. They enjoy concrete theoretical performance guarantees and sometimes provide strong empirical downstream gains, including for scalable approximate inference on graphs. We reach surprising conclusions about the benefits and limitations of variance reduction as a paradigm.

Universal Graph Random Features

We propose a novel random walk-based algorithm for unbiased estimation of arbitrary functions of a weighted adjacency matrix, coined universal graph random features (u-GRFs). This includes many of the most popular examples of kernels defined on the nodes of a graph. Our algorithm enjoys subquadratic time complexity with respect to the number of nodes, overcoming the notoriously prohibitive cubic scaling of exact graph kernel evaluation. It can also be trivially distributed across machines, permitting learning on much larger networks. At the heart of the algorithm is a modulation function which upweights or downweights the contribution from different random walks depending on their lengths. We show that by parameterising it with a neural network we can obtain u-GRFs that give higher-quality kernel estimates or perform efficient, scalable kernel learning. We provide robust theoretical analysis and support our findings with experiments including pointwise estimation of fixed graph kernels, solving non-homogeneous graph ordinary differential equations, node clustering and kernel regression on triangular meshes.

Repelling Random Walks

We present a novel quasi-Monte Carlo mechanism to improve graph-based sampling, coined repelling random walks. By inducing correlations between the trajectories of an interacting ensemble such that their marginal transition probabilities are unmodified, we are able to explore the graph more efficiently, improving the concentration of statistical estimators whilst leaving them unbiased. The mechanism has a trivial drop-in implementation. We showcase the effectiveness of repelling random walks in a range of settings including estimation of graph kernels, the PageRank vector and graphlet concentrations. We provide detailed experimental evaluation and robust theoretical guarantees. To our knowledge, repelling random walks constitute the first rigorously studied quasi-Monte Carlo scheme correlating the directions of walkers on a graph, inviting new research in this exciting nascent domain.

Quasi-Monte Carlo Graph Random Features

We present a novel mechanism to improve the accuracy of the recently-introduced class of graph random features (GRFs). Our method induces negative correlations between the lengths of the algorithm's random walks by imposing antithetic termination: a procedure to sample more diverse random walks which may be of independent interest. It has a trivial drop-in implementation. We derive strong theoretical guarantees on the properties of these quasi-Monte Carlo GRFs (q-GRFs), proving that they yield lower-variance estimators of the 2-regularised Laplacian kernel under mild conditions. Remarkably, our results hold for any graph topology. We demonstrate empirical accuracy improvements on a variety of tasks including a new practical application: time-efficient approximation of the graph diffusion process. To our knowledge, q-GRFs constitute the first rigorously studied quasi-Monte Carlo scheme for kernels defined on combinatorial objects, inviting new research on correlations between graph random walks.

Simplex Random Features

We present Simplex Random Features (SimRFs), a new random feature (RF) mechanism for unbiased approximation of the softmax and Gaussian kernels by geometrical correlation of random projection vectors. We prove that SimRFs provide the smallest possible mean square error (MSE) on unbiased estimates of these kernels among the class of weight-independent geometrically-coupled positive random feature (PRF) mechanisms, substantially outperforming the previously most accurate Orthogonal Random Features at no observable extra cost. We present a more computationally expensive SimRFs+ variant, which we prove is asymptotically optimal in the broader family of weight-dependent geometrical coupling schemes (which permit correlations between random vector directions and norms). In extensive empirical studies, we show consistent gains provided by SimRFs in settings including pointwise kernel estimation, nonparametric classification and scalable Transformers.

Why Flatness Correlates With Generalization For Deep Neural Networks

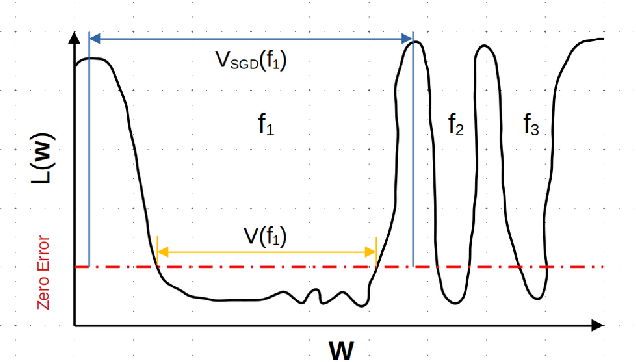
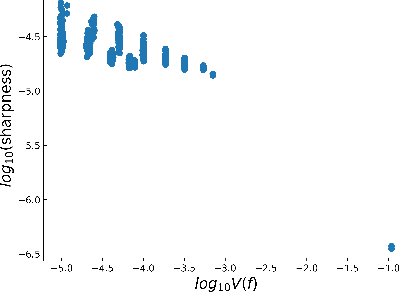
The intuition that local flatness of the loss landscape is correlated with better generalization for deep neural networks (DNNs) has been explored for decades, spawning many different local flatness measures. Here we argue that these measures correlate with generalization because they are local approximations to a global property, the volume of the set of parameters mapping to a specific function. This global volume is equivalent to the Bayesian prior upon initialization. For functions that give zero error on a test set, it is directly proportional to the Bayesian posterior, making volume a more robust and theoretically better grounded predictor of generalization than flatness. Whilst flatness measures fail under parameter re-scaling, volume remains invariant and therefore continues to correlate well with generalization. Moreover, some variants of SGD can break the flatness-generalization correlation, while the volume-generalization correlation remains intact.