Stratis Markou
Skillful joint probabilistic weather forecasting from marginals
Jun 12, 2025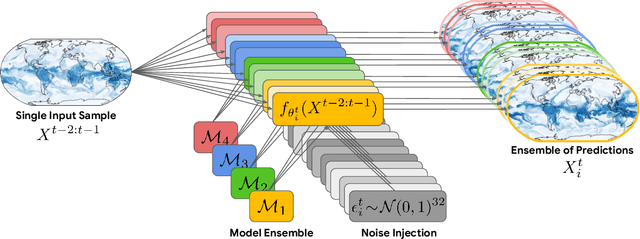
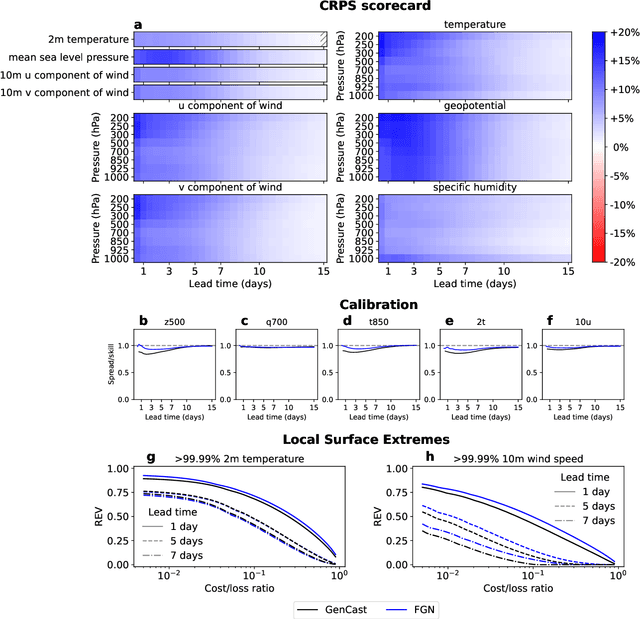
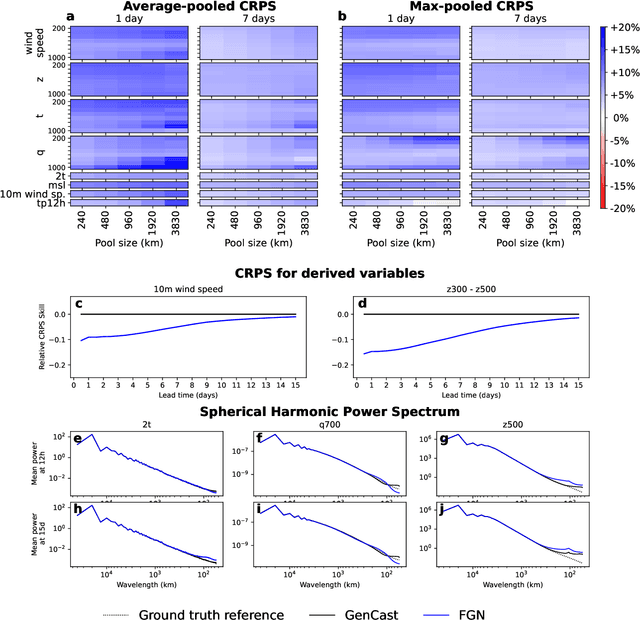
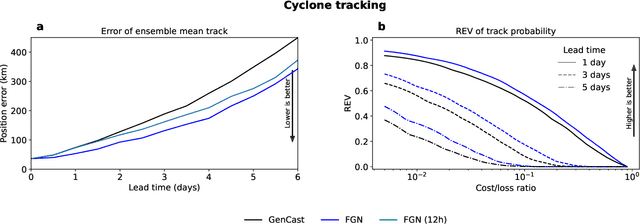
Abstract:Machine learning (ML)-based weather models have rapidly risen to prominence due to their greater accuracy and speed than traditional forecasts based on numerical weather prediction (NWP), recently outperforming traditional ensembles in global probabilistic weather forecasting. This paper presents FGN, a simple, scalable and flexible modeling approach which significantly outperforms the current state-of-the-art models. FGN generates ensembles via learned model-perturbations with an ensemble of appropriately constrained models. It is trained directly to minimize the continuous rank probability score (CRPS) of per-location forecasts. It produces state-of-the-art ensemble forecasts as measured by a range of deterministic and probabilistic metrics, makes skillful ensemble tropical cyclone track predictions, and captures joint spatial structure despite being trained only on marginals.
Translation Equivariant Transformer Neural Processes
Jun 18, 2024



Abstract:The effectiveness of neural processes (NPs) in modelling posterior prediction maps -- the mapping from data to posterior predictive distributions -- has significantly improved since their inception. This improvement can be attributed to two principal factors: (1) advancements in the architecture of permutation invariant set functions, which are intrinsic to all NPs; and (2) leveraging symmetries present in the true posterior predictive map, which are problem dependent. Transformers are a notable development in permutation invariant set functions, and their utility within NPs has been demonstrated through the family of models we refer to as TNPs. Despite significant interest in TNPs, little attention has been given to incorporating symmetries. Notably, the posterior prediction maps for data that are stationary -- a common assumption in spatio-temporal modelling -- exhibit translation equivariance. In this paper, we introduce of a new family of translation equivariant TNPs that incorporate translation equivariance. Through an extensive range of experiments on synthetic and real-world spatio-temporal data, we demonstrate the effectiveness of TE-TNPs relative to their non-translation-equivariant counterparts and other NP baselines.
Noise-Aware Differentially Private Regression via Meta-Learning
Jun 12, 2024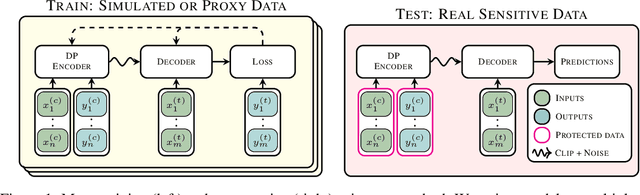
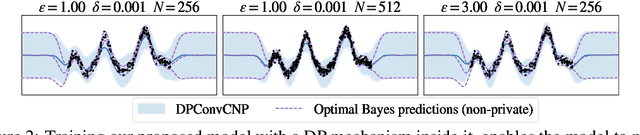

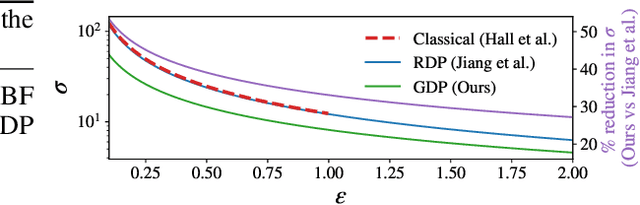
Abstract:Many high-stakes applications require machine learning models that protect user privacy and provide well-calibrated, accurate predictions. While Differential Privacy (DP) is the gold standard for protecting user privacy, standard DP mechanisms typically significantly impair performance. One approach to mitigating this issue is pre-training models on simulated data before DP learning on the private data. In this work we go a step further, using simulated data to train a meta-learning model that combines the Convolutional Conditional Neural Process (ConvCNP) with an improved functional DP mechanism of Hall et al. [2013] yielding the DPConvCNP. DPConvCNP learns from simulated data how to map private data to a DP predictive model in one forward pass, and then provides accurate, well-calibrated predictions. We compare DPConvCNP with a DP Gaussian Process (GP) baseline with carefully tuned hyperparameters. The DPConvCNP outperforms the GP baseline, especially on non-Gaussian data, yet is much faster at test time and requires less tuning.
Variance-Reducing Couplings for Random Features: Perspectives from Optimal Transport
May 26, 2024



Abstract:Random features (RFs) are a popular technique to scale up kernel methods in machine learning, replacing exact kernel evaluations with stochastic Monte Carlo estimates. They underpin models as diverse as efficient transformers (by approximating attention) to sparse spectrum Gaussian processes (by approximating the covariance function). Efficiency can be further improved by speeding up the convergence of these estimates: a variance reduction problem. We tackle this through the unifying framework of optimal transport, using theoretical insights and numerical algorithms to develop novel, high-performing RF couplings for kernels defined on Euclidean and discrete input spaces. They enjoy concrete theoretical performance guarantees and sometimes provide strong empirical downstream gains, including for scalable approximate inference on graphs. We reach surprising conclusions about the benefits and limitations of variance reduction as a paradigm.
Aardvark Weather: end-to-end data-driven weather forecasting
Mar 30, 2024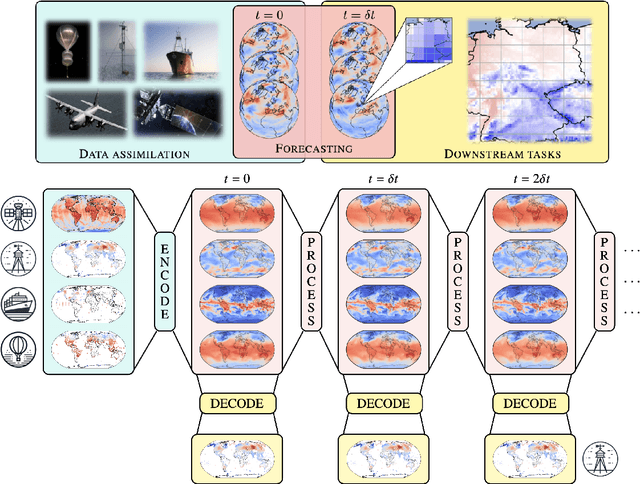
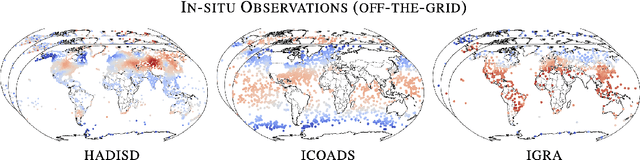
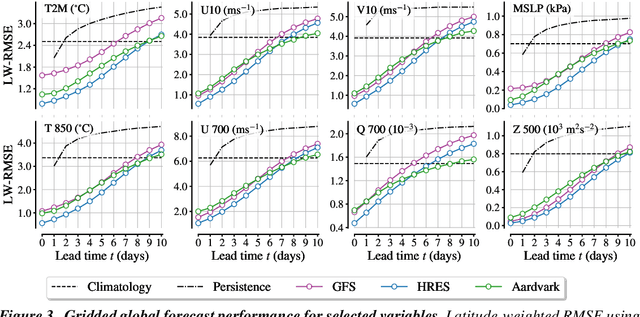
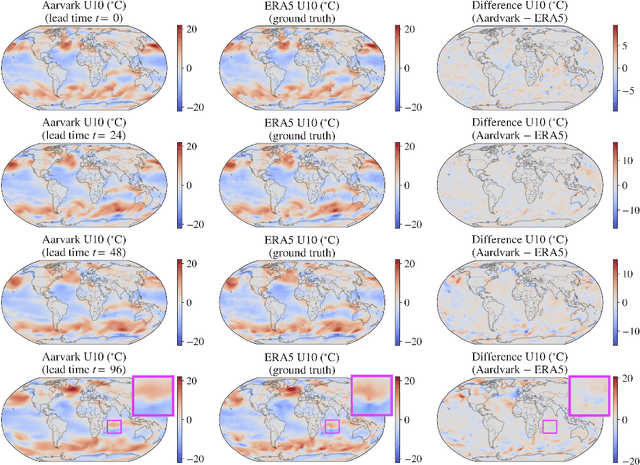
Abstract:Machine learning is revolutionising medium-range weather prediction. However it has only been applied to specific and individual components of the weather prediction pipeline. Consequently these data-driven approaches are unable to be deployed without input from conventional operational numerical weather prediction (NWP) systems, which is computationally costly and does not support end-to-end optimisation. In this work, we take a radically different approach and replace the entire NWP pipeline with a machine learning model. We present Aardvark Weather, the first end-to-end data-driven forecasting system which takes raw observations as input and provides both global and local forecasts. These global forecasts are produced for 24 variables at multiple pressure levels at one-degree spatial resolution and 24 hour temporal resolution, and are skillful with respect to hourly climatology at five to seven day lead times. Local forecasts are produced for temperature, mean sea level pressure, and wind speed at a geographically diverse set of weather stations, and are skillful with respect to an IFS-HRES interpolation baseline at multiple lead-times. Aardvark, by virtue of its simplicity and scalability, opens the door to a new paradigm for performing accurate and efficient data-driven medium-range weather forecasting.
Denoising Diffusion Probabilistic Models in Six Simple Steps
Feb 10, 2024Abstract:Denoising Diffusion Probabilistic Models (DDPMs) are a very popular class of deep generative model that have been successfully applied to a diverse range of problems including image and video generation, protein and material synthesis, weather forecasting, and neural surrogates of partial differential equations. Despite their ubiquity it is hard to find an introduction to DDPMs which is simple, comprehensive, clean and clear. The compact explanations necessary in research papers are not able to elucidate all of the different design steps taken to formulate the DDPM and the rationale of the steps that are presented is often omitted to save space. Moreover, the expositions are typically presented from the variational lower bound perspective which is unnecessary and arguably harmful as it obfuscates why the method is working and suggests generalisations that do not perform well in practice. On the other hand, perspectives that take the continuous time-limit are beautiful and general, but they have a high barrier-to-entry as they require background knowledge of stochastic differential equations and probability flow. In this note, we distill down the formulation of the DDPM into six simple steps each of which comes with a clear rationale. We assume that the reader is familiar with fundamental topics in machine learning including basic probabilistic modelling, Gaussian distributions, maximum likelihood estimation, and deep learning.
Autoregressive Conditional Neural Processes
Mar 25, 2023

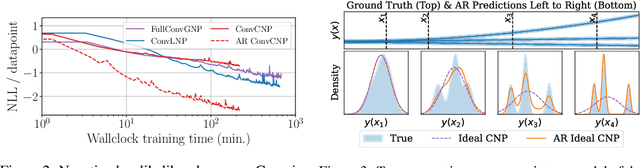
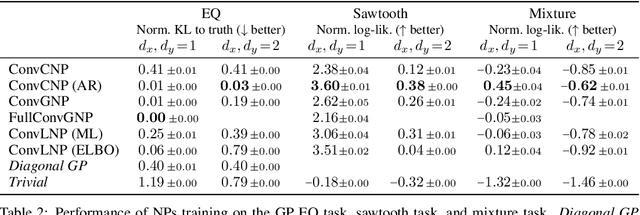
Abstract:Conditional neural processes (CNPs; Garnelo et al., 2018a) are attractive meta-learning models which produce well-calibrated predictions and are trainable via a simple maximum likelihood procedure. Although CNPs have many advantages, they are unable to model dependencies in their predictions. Various works propose solutions to this, but these come at the cost of either requiring approximate inference or being limited to Gaussian predictions. In this work, we instead propose to change how CNPs are deployed at test time, without any modifications to the model or training procedure. Instead of making predictions independently for every target point, we autoregressively define a joint predictive distribution using the chain rule of probability, taking inspiration from the neural autoregressive density estimator (NADE) literature. We show that this simple procedure allows factorised Gaussian CNPs to model highly dependent, non-Gaussian predictive distributions. Perhaps surprisingly, in an extensive range of tasks with synthetic and real data, we show that CNPs in autoregressive (AR) mode not only significantly outperform non-AR CNPs, but are also competitive with more sophisticated models that are significantly more computationally expensive and challenging to train. This performance is remarkable given that AR CNPs are not trained to model joint dependencies. Our work provides an example of how ideas from neural distribution estimation can benefit neural processes, and motivates research into the AR deployment of other neural process models.
Trieste: Efficiently Exploring The Depths of Black-box Functions with TensorFlow
Feb 16, 2023Abstract:We present Trieste, an open-source Python package for Bayesian optimization and active learning benefiting from the scalability and efficiency of TensorFlow. Our library enables the plug-and-play of popular TensorFlow-based models within sequential decision-making loops, e.g. Gaussian processes from GPflow or GPflux, or neural networks from Keras. This modular mindset is central to the package and extends to our acquisition functions and the internal dynamics of the decision-making loop, both of which can be tailored and extended by researchers or engineers when tackling custom use cases. Trieste is a research-friendly and production-ready toolkit backed by a comprehensive test suite, extensive documentation, and available at https://github.com/secondmind-labs/trieste.
Active Learning with Convolutional Gaussian Neural Processes for Environmental Sensor Placement
Nov 22, 2022Abstract:Deploying environmental measurement stations can be a costly and time-consuming procedure, especially in remote regions that are difficult to access, such as Antarctica. Therefore, it is crucial that sensors are placed as efficiently as possible, maximising the informativeness of their measurements. This can be tackled by fitting a probabilistic model to existing data and identifying placements that would maximally reduce the model's uncertainty. The models most widely used for this purpose are Gaussian processes (GPs). However, designing a GP covariance which captures the complex behaviour of non-stationary spatiotemporal data is a difficult task. Further, the computational cost of GPs makes them challenging to scale to large environmental datasets. In this work, we explore using a convolutional Gaussian neural process (ConvGNP) to address these issues. A ConvGNP is a meta-learning model that uses neural networks to parameterise a GP predictive. Our model is data-driven, flexible, efficient, and permits multiple input predictors of gridded or scattered modalities. Using simulated surface air temperature fields over Antarctica as ground truth, we show that a ConvGNP significantly outperforms a non-stationary GP baseline in terms of predictive performance. We then use the ConvGNP in an Antarctic sensor placement toy experiment, yielding promising results.
Practical Conditional Neural Processes Via Tractable Dependent Predictions
Mar 16, 2022
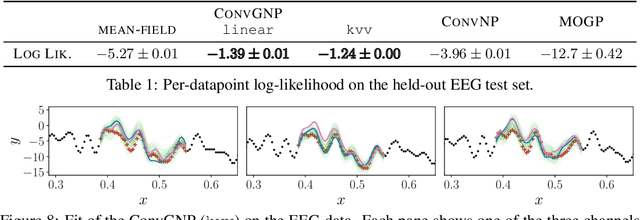
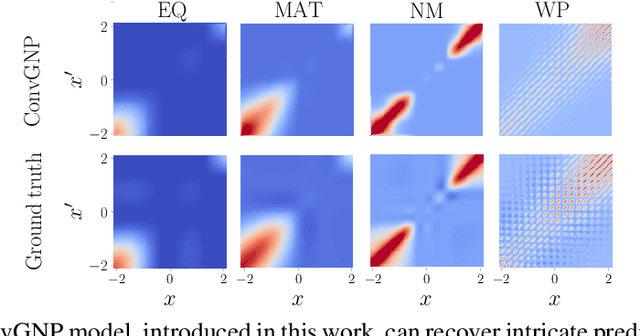

Abstract:Conditional Neural Processes (CNPs; Garnelo et al., 2018a) are meta-learning models which leverage the flexibility of deep learning to produce well-calibrated predictions and naturally handle off-the-grid and missing data. CNPs scale to large datasets and train with ease. Due to these features, CNPs appear well-suited to tasks from environmental sciences or healthcare. Unfortunately, CNPs do not produce correlated predictions, making them fundamentally inappropriate for many estimation and decision making tasks. Predicting heat waves or floods, for example, requires modelling dependencies in temperature or precipitation over time and space. Existing approaches which model output dependencies, such as Neural Processes (NPs; Garnelo et al., 2018b) or the FullConvGNP (Bruinsma et al., 2021), are either complicated to train or prohibitively expensive. What is needed is an approach which provides dependent predictions, but is simple to train and computationally tractable. In this work, we present a new class of Neural Process models that make correlated predictions and support exact maximum likelihood training that is simple and scalable. We extend the proposed models by using invertible output transformations, to capture non-Gaussian output distributions. Our models can be used in downstream estimation tasks which require dependent function samples. By accounting for output dependencies, our models show improved predictive performance on a range of experiments with synthetic and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge