On conditional diffusion models for PDE simulations

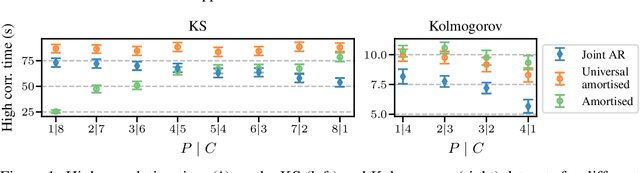
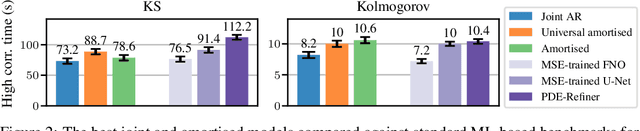
Modelling partial differential equations (PDEs) is of crucial importance in science and engineering, and it includes tasks ranging from forecasting to inverse problems, such as data assimilation. However, most previous numerical and machine learning approaches that target forecasting cannot be applied out-of-the-box for data assimilation. Recently, diffusion models have emerged as a powerful tool for conditional generation, being able to flexibly incorporate observations without retraining. In this work, we perform a comparative study of score-based diffusion models for forecasting and assimilation of sparse observations. In particular, we focus on diffusion models that are either trained in a conditional manner, or conditioned after unconditional training. We address the shortcomings of existing models by proposing 1) an autoregressive sampling approach that significantly improves performance in forecasting, 2) a new training strategy for conditional score-based models that achieves stable performance over a range of history lengths, and 3) a hybrid model which employs flexible pre-training conditioning on initial conditions and flexible post-training conditioning to handle data assimilation. We empirically show that these modifications are crucial for successfully tackling the combination of forecasting and data assimilation, a task commonly encountered in real-world scenarios.

Gridded Transformer Neural Processes for Large Unstructured Spatio-Temporal Data

Many important problems require modelling large-scale spatio-temporal datasets, with one prevalent example being weather forecasting. Recently, transformer-based approaches have shown great promise in a range of weather forecasting problems. However, these have mostly focused on gridded data sources, neglecting the wealth of unstructured, off-the-grid data from observational measurements such as those at weather stations. A promising family of models suitable for such tasks are neural processes (NPs), notably the family of transformer neural processes (TNPs). Although TNPs have shown promise on small spatio-temporal datasets, they are unable to scale to the quantities of data used by state-of-the-art weather and climate models. This limitation stems from their lack of efficient attention mechanisms. We address this shortcoming through the introduction of gridded pseudo-token TNPs which employ specialised encoders and decoders to handle unstructured observations and utilise a processor containing gridded pseudo-tokens that leverage efficient attention mechanisms. Our method consistently outperforms a range of strong baselines on various synthetic and real-world regression tasks involving large-scale data, while maintaining competitive computational efficiency. The real-life experiments are performed on weather data, demonstrating the potential of our approach to bring performance and computational benefits when applied at scale in a weather modelling pipeline.

Approximately Equivariant Neural Processes

Equivariant deep learning architectures exploit symmetries in learning problems to improve the sample efficiency of neural-network-based models and their ability to generalise. However, when modelling real-world data, learning problems are often not exactly equivariant, but only approximately. For example, when estimating the global temperature field from weather station observations, local topographical features like mountains break translation equivariance. In these scenarios, it is desirable to construct architectures that can flexibly depart from exact equivariance in a data-driven way. In this paper, we develop a general approach to achieving this using existing equivariant architectures. Our approach is agnostic to both the choice of symmetry group and model architecture, making it widely applicable. We consider the use of approximately equivariant architectures in neural processes (NPs), a popular family of meta-learning models. We demonstrate the effectiveness of our approach on a number of synthetic and real-world regression experiments, demonstrating that approximately equivariant NP models can outperform both their non-equivariant and strictly equivariant counterparts.

In-Context In-Context Learning with Transformer Neural Processes

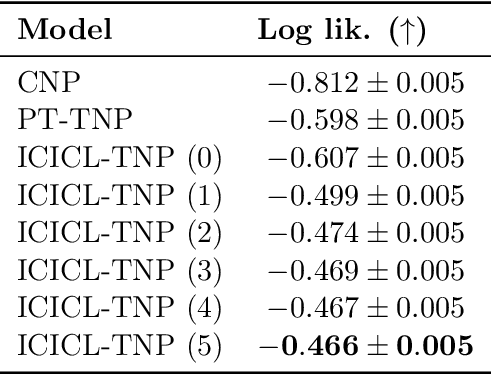
Neural processes (NPs) are a powerful family of meta-learning models that seek to approximate the posterior predictive map of the ground-truth stochastic process from which each dataset in a meta-dataset is sampled. There are many cases in which practitioners, besides having access to the dataset of interest, may also have access to other datasets that share similarities with it. In this case, integrating these datasets into the NP can improve predictions. We equip NPs with this functionality and describe this paradigm as in-context in-context learning. Standard NP architectures, such as the convolutional conditional NP (ConvCNP) or the family of transformer neural processes (TNPs), are not capable of in-context in-context learning, as they are only able to condition on a single dataset. We address this shortcoming by developing the in-context in-context learning pseudo-token TNP (ICICL-TNP). The ICICL-TNP builds on the family of PT-TNPs, which utilise pseudo-token-based transformer architectures to sidestep the quadratic computational complexity associated with regular transformer architectures. Importantly, the ICICL-TNP is capable of conditioning on both sets of datapoints and sets of datasets, enabling it to perform in-context in-context learning. We demonstrate the importance of in-context in-context learning and the effectiveness of the ICICL-TNP in a number of experiments.

Translation Equivariant Transformer Neural Processes

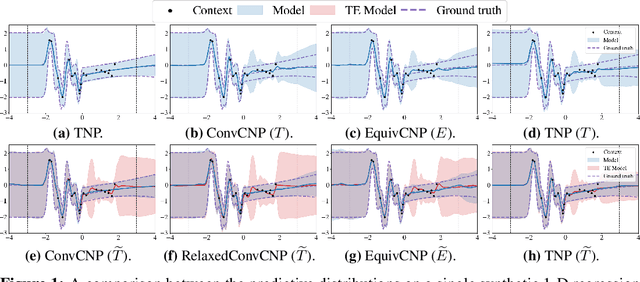
The effectiveness of neural processes (NPs) in modelling posterior prediction maps -- the mapping from data to posterior predictive distributions -- has significantly improved since their inception. This improvement can be attributed to two principal factors: (1) advancements in the architecture of permutation invariant set functions, which are intrinsic to all NPs; and (2) leveraging symmetries present in the true posterior predictive map, which are problem dependent. Transformers are a notable development in permutation invariant set functions, and their utility within NPs has been demonstrated through the family of models we refer to as TNPs. Despite significant interest in TNPs, little attention has been given to incorporating symmetries. Notably, the posterior prediction maps for data that are stationary -- a common assumption in spatio-temporal modelling -- exhibit translation equivariance. In this paper, we introduce of a new family of translation equivariant TNPs that incorporate translation equivariance. Through an extensive range of experiments on synthetic and real-world spatio-temporal data, we demonstrate the effectiveness of TE-TNPs relative to their non-translation-equivariant counterparts and other NP baselines.