On conditional diffusion models for PDE simulations

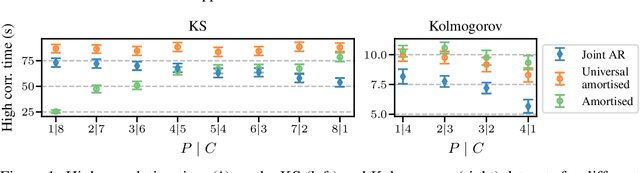
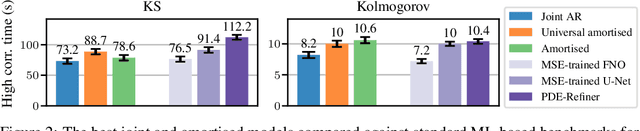
Modelling partial differential equations (PDEs) is of crucial importance in science and engineering, and it includes tasks ranging from forecasting to inverse problems, such as data assimilation. However, most previous numerical and machine learning approaches that target forecasting cannot be applied out-of-the-box for data assimilation. Recently, diffusion models have emerged as a powerful tool for conditional generation, being able to flexibly incorporate observations without retraining. In this work, we perform a comparative study of score-based diffusion models for forecasting and assimilation of sparse observations. In particular, we focus on diffusion models that are either trained in a conditional manner, or conditioned after unconditional training. We address the shortcomings of existing models by proposing 1) an autoregressive sampling approach that significantly improves performance in forecasting, 2) a new training strategy for conditional score-based models that achieves stable performance over a range of history lengths, and 3) a hybrid model which employs flexible pre-training conditioning on initial conditions and flexible post-training conditioning to handle data assimilation. We empirically show that these modifications are crucial for successfully tackling the combination of forecasting and data assimilation, a task commonly encountered in real-world scenarios.

Riemannian Laplace approximations for Bayesian neural networks

Bayesian neural networks often approximate the weight-posterior with a Gaussian distribution. However, practical posteriors are often, even locally, highly non-Gaussian, and empirical performance deteriorates. We propose a simple parametric approximate posterior that adapts to the shape of the true posterior through a Riemannian metric that is determined by the log-posterior gradient. We develop a Riemannian Laplace approximation where samples naturally fall into weight-regions with low negative log-posterior. We show that these samples can be drawn by solving a system of ordinary differential equations, which can be done efficiently by leveraging the structure of the Riemannian metric and automatic differentiation. Empirically, we demonstrate that our approach consistently improves over the conventional Laplace approximation across tasks. We further show that, unlike the conventional Laplace approximation, our method is not overly sensitive to the choice of prior, which alleviates a practical pitfall of current approaches.

Model-agnostic out-of-distribution detection using combined statistical tests

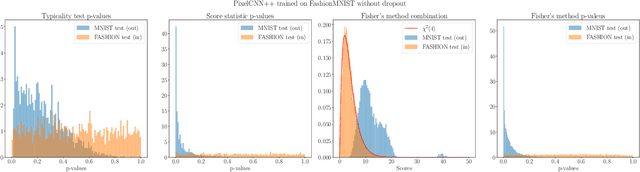
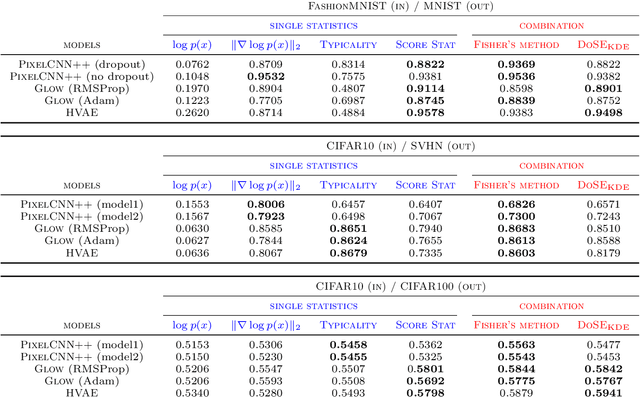
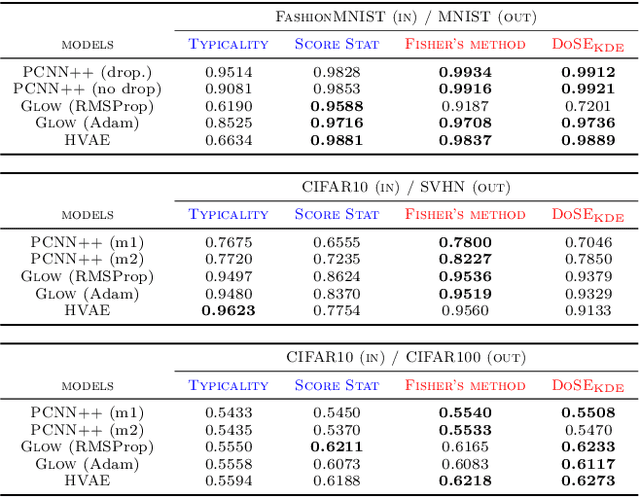
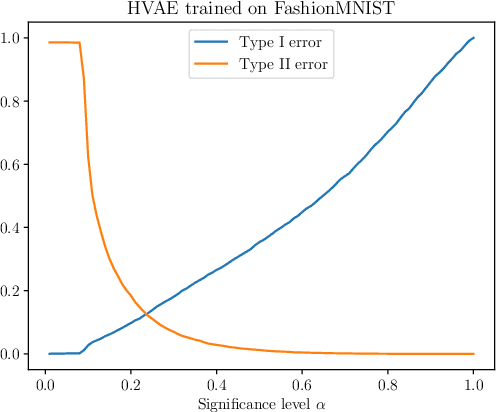
We present simple methods for out-of-distribution detection using a trained generative model. These techniques, based on classical statistical tests, are model-agnostic in the sense that they can be applied to any differentiable generative model. The idea is to combine a classical parametric test (Rao's score test) with the recently introduced typicality test. These two test statistics are both theoretically well-founded and exploit different sources of information based on the likelihood for the typicality test and its gradient for the score test. We show that combining them using Fisher's method overall leads to a more accurate out-of-distribution test. We also discuss the benefits of casting out-of-distribution detection as a statistical testing problem, noting in particular that false positive rate control can be valuable for practical out-of-distribution detection. Despite their simplicity and generality, these methods can be competitive with model-specific out-of-distribution detection algorithms without any assumptions on the out-distribution.