ChronosX: Adapting Pretrained Time Series Models with Exogenous Variables

Covariates provide valuable information on external factors that influence time series and are critical in many real-world time series forecasting tasks. For example, in retail, covariates may indicate promotions or peak dates such as holiday seasons that heavily influence demand forecasts. Recent advances in pretraining large language model architectures for time series forecasting have led to highly accurate forecasters. However, the majority of these models do not readily use covariates as they are often specific to a certain task or domain. This paper introduces a new method to incorporate covariates into pretrained time series forecasting models. Our proposed approach incorporates covariate information into pretrained forecasting models through modular blocks that inject past and future covariate information, without necessarily modifying the pretrained model in consideration. In order to evaluate our approach, we introduce a benchmark composed of 32 different synthetic datasets with varying dynamics to evaluate the effectivity of forecasting models with covariates. Extensive evaluations on both synthetic and real datasets show that our approach effectively incorporates covariate information into pretrained models, outperforming existing baselines.

Learning Energy-Based Models by Self-normalising the Likelihood

Training an energy-based model (EBM) with maximum likelihood is challenging due to the intractable normalisation constant. Traditional methods rely on expensive Markov chain Monte Carlo (MCMC) sampling to estimate the gradient of logartihm of the normalisation constant. We propose a novel objective called self-normalised log-likelihood (SNL) that introduces a single additional learnable parameter representing the normalisation constant compared to the regular log-likelihood. SNL is a lower bound of the log-likelihood, and its optimum corresponds to both the maximum likelihood estimate of the model parameters and the normalisation constant. We show that the SNL objective is concave in the model parameters for exponential family distributions. Unlike the regular log-likelihood, the SNL can be directly optimised using stochastic gradient techniques by sampling from a crude proposal distribution. We validate the effectiveness of our proposed method on various density estimation tasks as well as EBMs for regression. Our results show that the proposed method, while simpler to implement and tune, outperforms existing techniques.

Model-agnostic out-of-distribution detection using combined statistical tests

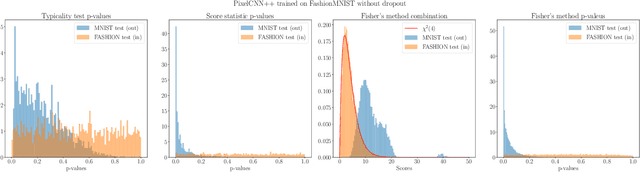
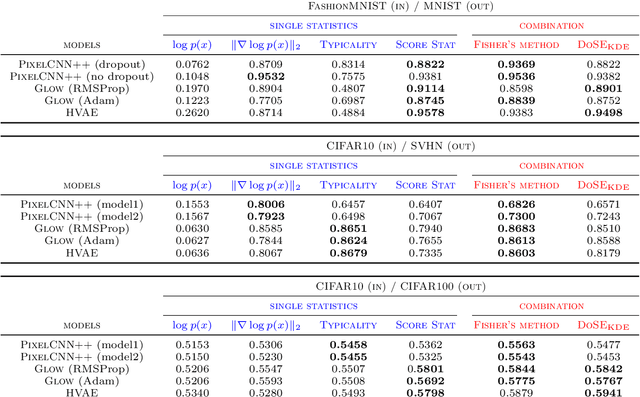
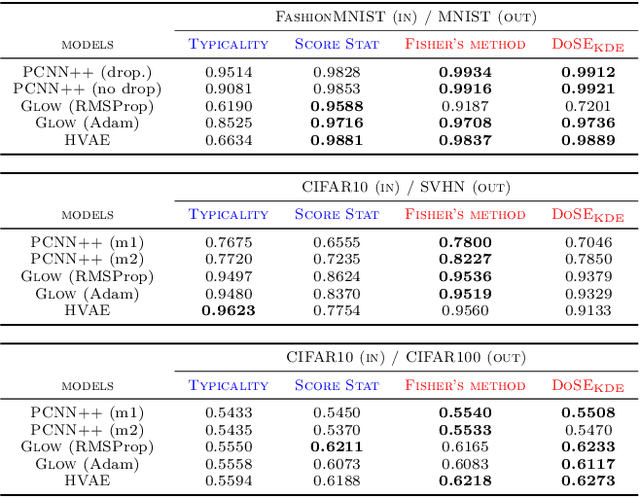
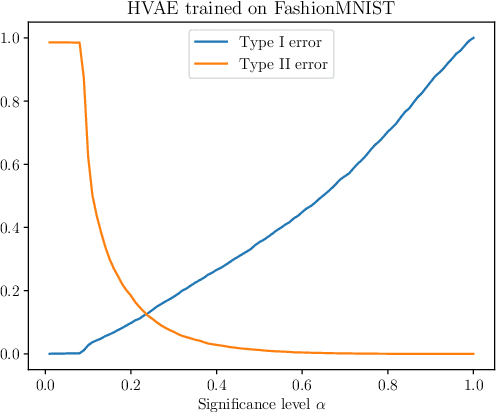
We present simple methods for out-of-distribution detection using a trained generative model. These techniques, based on classical statistical tests, are model-agnostic in the sense that they can be applied to any differentiable generative model. The idea is to combine a classical parametric test (Rao's score test) with the recently introduced typicality test. These two test statistics are both theoretically well-founded and exploit different sources of information based on the likelihood for the typicality test and its gradient for the score test. We show that combining them using Fisher's method overall leads to a more accurate out-of-distribution test. We also discuss the benefits of casting out-of-distribution detection as a statistical testing problem, noting in particular that false positive rate control can be valuable for practical out-of-distribution detection. Despite their simplicity and generality, these methods can be competitive with model-specific out-of-distribution detection algorithms without any assumptions on the out-distribution.