Chronos: Learning the Language of Time Series

We introduce Chronos, a simple yet effective framework for pretrained probabilistic time series models. Chronos tokenizes time series values using scaling and quantization into a fixed vocabulary and trains existing transformer-based language model architectures on these tokenized time series via the cross-entropy loss. We pretrained Chronos models based on the T5 family (ranging from 20M to 710M parameters) on a large collection of publicly available datasets, complemented by a synthetic dataset that we generated via Gaussian processes to improve generalization. In a comprehensive benchmark consisting of 42 datasets, and comprising both classical local models and deep learning methods, we show that Chronos models: (a) significantly outperform other methods on datasets that were part of the training corpus; and (b) have comparable and occasionally superior zero-shot performance on new datasets, relative to methods that were trained specifically on them. Our results demonstrate that Chronos models can leverage time series data from diverse domains to improve zero-shot accuracy on unseen forecasting tasks, positioning pretrained models as a viable tool to greatly simplify forecasting pipelines.

Generalized Matrix Means for Semi-Supervised Learning with Multilayer Graphs

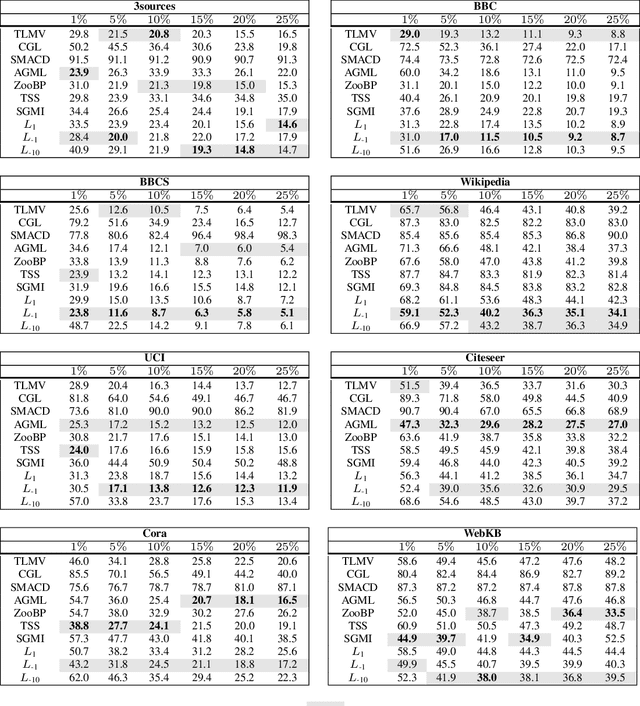
We study the task of semi-supervised learning on multilayer graphs by taking into account both labeled and unlabeled observations together with the information encoded by each individual graph layer. We propose a regularizer based on the generalized matrix mean, which is a one-parameter family of matrix means that includes the arithmetic, geometric and harmonic means as particular cases. We analyze it in expectation under a Multilayer Stochastic Block Model and verify numerically that it outperforms state of the art methods. Moreover, we introduce a matrix-free numerical scheme based on contour integral quadratures and Krylov subspace solvers that scales to large sparse multilayer graphs.

Spectral Clustering of Signed Graphs via Matrix Power Means

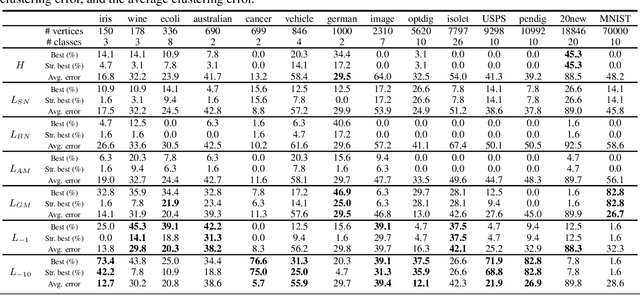
Signed graphs encode positive (attractive) and negative (repulsive) relations between nodes. We extend spectral clustering to signed graphs via the one-parameter family of Signed Power Mean Laplacians, defined as the matrix power mean of normalized standard and signless Laplacians of positive and negative edges. We provide a thorough analysis of the proposed approach in the setting of a general Stochastic Block Model that includes models such as the Labeled Stochastic Block Model and the Censored Block Model. We show that in expectation the signed power mean Laplacian captures the ground truth clusters under reasonable settings where state-of-the-art approaches fail. Moreover, we prove that the eigenvalues and eigenvector of the signed power mean Laplacian concentrate around their expectation under reasonable conditions in the general Stochastic Block Model. Extensive experiments on random graphs and real world datasets confirm the theoretically predicted behaviour of the signed power mean Laplacian and show that it compares favourably with state-of-the-art methods.

Community detection in networks via nonlinear modularity eigenvectors

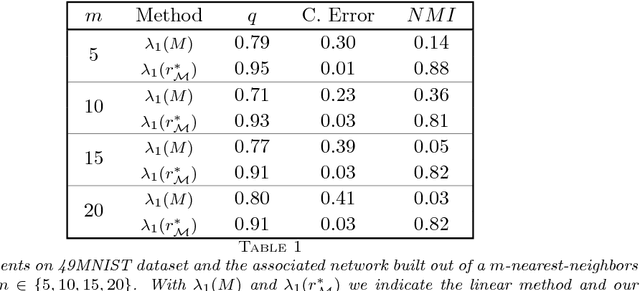
Revealing a community structure in a network or dataset is a central problem arising in many scientific areas. The modularity function $Q$ is an established measure quantifying the quality of a community, being identified as a set of nodes having high modularity. In our terminology, a set of nodes with positive modularity is called a \textit{module} and a set that maximizes $Q$ is thus called \textit{leading module}. Finding a leading module in a network is an important task, however the dimension of real-world problems makes the maximization of $Q$ unfeasible. This poses the need of approximation techniques which are typically based on a linear relaxation of $Q$, induced by the spectrum of the modularity matrix $M$. In this work we propose a nonlinear relaxation which is instead based on the spectrum of a nonlinear modularity operator $\mathcal M$. We show that extremal eigenvalues of $\mathcal M$ provide an exact relaxation of the modularity measure $Q$, however at the price of being more challenging to be computed than those of $M$. Thus we extend the work made on nonlinear Laplacians, by proposing a computational scheme, named \textit{generalized RatioDCA}, to address such extremal eigenvalues. We show monotonic ascent and convergence of the method. We finally apply the new method to several synthetic and real-world data sets, showing both effectiveness of the model and performance of the method.

Node classification for signed networks using diffuse interface methods

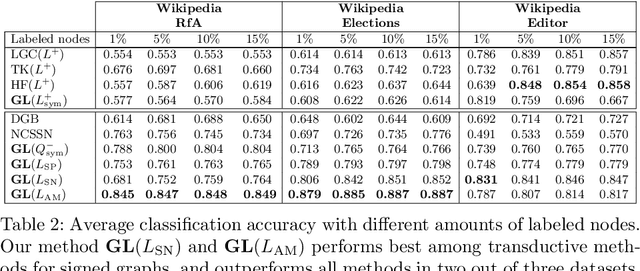
Signed networks are a crucial tool when modeling friend and foe relationships. In contrast to classical undirected, weighted graphs, the edge weights for signed graphs are positive and negative. Crucial network properties are often derived from the study of the associated graph Laplacians. We here study several different signed network Laplacians with a focus on the task of classifying the nodes of the graph. We here extend a recently introduced technique based on a partial differential equation defined on the signed network, namely the Allen-Cahn-equation, to classify the nodes into two or more classes. We illustrate the performance of this approach on several real-world networks.

The Power Mean Laplacian for Multilayer Graph Clustering

Multilayer graphs encode different kind of interactions between the same set of entities. When one wants to cluster such a multilayer graph, the natural question arises how one should merge the information different layers. We introduce in this paper a one-parameter family of matrix power means for merging the Laplacians from different layers and analyze it in expectation in the stochastic block model. We show that this family allows to recover ground truth clusters under different settings and verify this in real world data. While computing the matrix power mean can be very expensive for large graphs, we introduce a numerical scheme to efficiently compute its eigenvectors for the case of large sparse graphs.

Clustering Signed Networks with the Geometric Mean of Laplacians

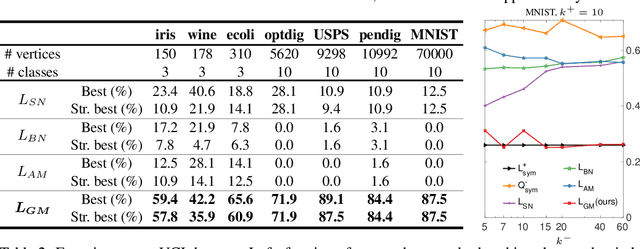
Signed networks allow to model positive and negative relationships. We analyze existing extensions of spectral clustering to signed networks. It turns out that existing approaches do not recover the ground truth clustering in several situations where either the positive or the negative network structures contain no noise. Our analysis shows that these problems arise as existing approaches take some form of arithmetic mean of the Laplacians of the positive and negative part. As a solution we propose to use the geometric mean of the Laplacians of positive and negative part and show that it outperforms the existing approaches. While the geometric mean of matrices is computationally expensive, we show that eigenvectors of the geometric mean can be computed efficiently, leading to a numerical scheme for sparse matrices which is of independent interest.