End-to-End Probabilistic Framework for Learning with Hard Constraints

We present a general purpose probabilistic forecasting framework, ProbHardE2E, to learn systems that can incorporate operational/physical constraints as hard requirements. ProbHardE2E enforces hard constraints by exploiting variance information in a novel way; and thus it is also capable of performing uncertainty quantification (UQ) on the model. Our methodology uses a novel differentiable probabilistic projection layer (DPPL) that can be combined with a wide range of neural network architectures. This DPPL allows the model to learn the system in an end-to-end manner, compared to other approaches where the constraints are satisfied either through a post-processing step or at inference. In addition, ProbHardE2E can optimize a strictly proper scoring rule, without making any distributional assumptions on the target, which enables it to obtain robust distributional estimates (in contrast to existing approaches that generally optimize likelihood-based objectives, which are heavily biased by their distributional assumptions and model choices); and it can incorporate a range of non-linear constraints (increasing the power of modeling and flexibility). We apply ProbHardE2E to problems in learning partial differential equations with uncertainty estimates and to probabilistic time-series forecasting, showcasing it as a broadly applicable general setup that connects these seemingly disparate domains.

ChronosX: Adapting Pretrained Time Series Models with Exogenous Variables

Covariates provide valuable information on external factors that influence time series and are critical in many real-world time series forecasting tasks. For example, in retail, covariates may indicate promotions or peak dates such as holiday seasons that heavily influence demand forecasts. Recent advances in pretraining large language model architectures for time series forecasting have led to highly accurate forecasters. However, the majority of these models do not readily use covariates as they are often specific to a certain task or domain. This paper introduces a new method to incorporate covariates into pretrained time series forecasting models. Our proposed approach incorporates covariate information into pretrained forecasting models through modular blocks that inject past and future covariate information, without necessarily modifying the pretrained model in consideration. In order to evaluate our approach, we introduce a benchmark composed of 32 different synthetic datasets with varying dynamics to evaluate the effectivity of forecasting models with covariates. Extensive evaluations on both synthetic and real datasets show that our approach effectively incorporates covariate information into pretrained models, outperforming existing baselines.

Enhancing Foundation Models for Time Series Forecasting via Wavelet-based Tokenization

How to best develop foundational models for time series forecasting remains an important open question. Tokenization is a crucial consideration in this effort: what is an effective discrete vocabulary for a real-valued sequential input? To address this question, we develop WaveToken, a wavelet-based tokenizer that allows models to learn complex representations directly in the space of time-localized frequencies. Our method first scales and decomposes the input time series, then thresholds and quantizes the wavelet coefficients, and finally pre-trains an autoregressive model to forecast coefficients for the forecast horizon. By decomposing coarse and fine structures in the inputs, wavelets provide an eloquent and compact language for time series forecasting that simplifies learning. Empirical results on a comprehensive benchmark, including 42 datasets for both in-domain and zero-shot settings, show that WaveToken: i) provides better accuracy than recently proposed foundation models for forecasting while using a much smaller vocabulary (1024 tokens), and performs on par or better than modern deep learning models trained specifically on each dataset; and ii) exhibits superior generalization capabilities, achieving the best average rank across all datasets for three complementary metrics. In addition, we show that our method can easily capture complex temporal patterns of practical relevance that are challenging for other recent pre-trained models, including trends, sparse spikes, and non-stationary time series with varying frequencies evolving over time.

Hard Constraint Guided Flow Matching for Gradient-Free Generation of PDE Solutions

Generative models that satisfy hard constraints are crucial in many scientific and engineering applications where physical laws or system requirements must be strictly respected. However, many existing constrained generative models, especially those developed for computer vision, rely heavily on gradient information, often sparse or computationally expensive in fields like partial differential equations (PDEs). In this work, we introduce a novel framework for adapting pre-trained, unconstrained flow-matching models to satisfy constraints exactly in a zero-shot manner without requiring expensive gradient computations or fine-tuning. Our framework, ECI sampling, alternates between extrapolation (E), correction (C), and interpolation (I) stages during each iterative sampling step of flow matching sampling to ensure accurate integration of constraint information while preserving the validity of the generation. We demonstrate the effectiveness of our approach across various PDE systems, showing that ECI-guided generation strictly adheres to physical constraints and accurately captures complex distribution shifts induced by these constraints. Empirical results demonstrate that our framework consistently outperforms baseline approaches in various zero-shot constrained generation tasks and also achieves competitive results in the regression tasks without additional fine-tuning.

AhmedML: High-Fidelity Computational Fluid Dynamics Dataset for Incompressible, Low-Speed Bluff Body Aerodynamics

The development of Machine Learning (ML) methods for Computational Fluid Dynamics (CFD) is currently limited by the lack of openly available training data. This paper presents a new open-source dataset comprising of high fidelity, scale-resolving CFD simulations of 500 geometric variations of the Ahmed Car Body - a simplified car-like shape that exhibits many of the flow topologies that are present on bluff bodies such as road vehicles. The dataset contains simulation results that exhibit a broad set of fundamental flow physics such as geometry and pressure-induced flow separation as well as 3D vortical structures. Each variation of the Ahmed car body were run using a high-fidelity, time-accurate, hybrid Reynolds-Averaged Navier-Stokes (RANS) - Large-Eddy Simulation (LES) turbulence modelling approach using the open-source CFD code OpenFOAM. The dataset contains boundary, volume, geometry, and time-averaged forces/moments in widely used open-source formats. In addition, the OpenFOAM case setup is provided so that others can reproduce or extend the dataset. This represents to the authors knowledge, the first open-source large-scale dataset using high-fidelity CFD methods for the widely used Ahmed car body that is available to freely download with a permissive license (CC-BY-SA).

WindsorML -- High-Fidelity Computational Fluid Dynamics Dataset For Automotive Aerodynamics

This paper presents a new open-source high-fidelity dataset for Machine Learning (ML) containing 355 geometric variants of the Windsor body, to help the development and testing of ML surrogate models for external automotive aerodynamics. Each Computational Fluid Dynamics (CFD) simulation was run with a GPU-native high-fidelity Wall-Modeled Large-Eddy Simulations (WMLES) using a Cartesian immersed-boundary method using more than 280M cells to ensure the greatest possible accuracy. The dataset contains geometry variants that exhibits a wide range of flow characteristics that are representative of those observed on road-cars. The dataset itself contains the 3D time-averaged volume & boundary data as well as the geometry and force & moment coefficients. This paper discusses the validation of the underlying CFD methods as well as contents and structure of the dataset. To the authors knowledge, this represents the first, large-scale high-fidelity CFD dataset for the Windsor body with a permissive open-source license (CC-BY-SA).

Comparing and Contrasting Deep Learning Weather Prediction Backbones on Navier-Stokes and Atmospheric Dynamics

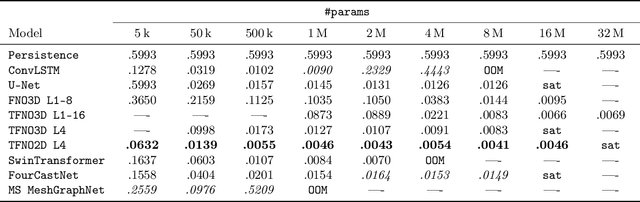
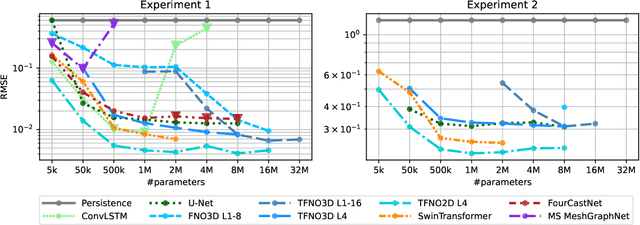
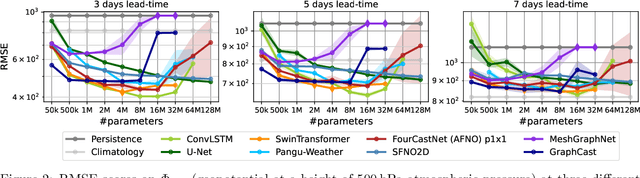
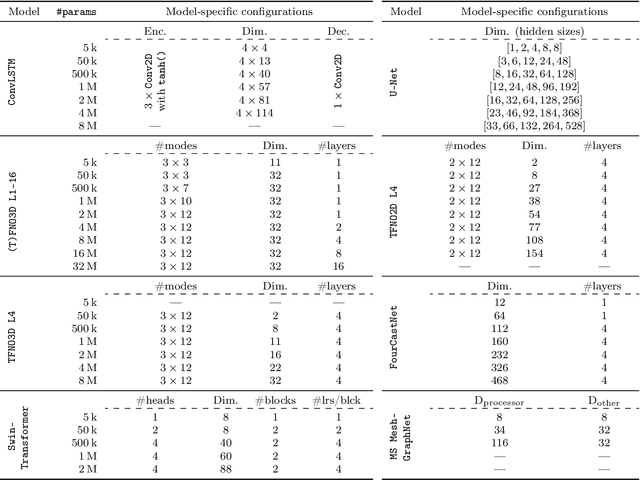
Remarkable progress in the development of Deep Learning Weather Prediction (DLWP) models positions them to become competitive with traditional numerical weather prediction (NWP) models. Indeed, a wide number of DLWP architectures -- based on various backbones, including U-Net, Transformer, Graph Neural Network (GNN), and Fourier Neural Operator (FNO) -- have demonstrated their potential at forecasting atmospheric states. However, due to differences in training protocols, forecast horizons, and data choices, it remains unclear which (if any) of these methods and architectures are most suitable for weather forecasting and for future model development. Here, we step back and provide a detailed empirical analysis, under controlled conditions, comparing and contrasting the most prominent DLWP models, along with their backbones. We accomplish this by predicting synthetic two-dimensional incompressible Navier-Stokes and real-world global weather dynamics. In terms of accuracy, memory consumption, and runtime, our results illustrate various tradeoffs. For example, on synthetic data, we observe favorable performance of FNO; and on the real-world WeatherBench dataset, our results demonstrate the suitability of ConvLSTM and SwinTransformer for short-to-mid-ranged forecasts. For long-ranged weather rollouts of up to 365 days, we observe superior stability and physical soundness in architectures that formulate a spherical data representation, i.e., GraphCast and Spherical FNO. In addition, we observe that all of these model backbones ``saturate,'' i.e., none of them exhibit so-called neural scaling, which highlights an important direction for future work on these and related models.

Transferring Knowledge from Large Foundation Models to Small Downstream Models

How do we transfer the relevant knowledge from ever larger foundation models into small, task-specific downstream models that can run at much lower costs? Standard transfer learning using pre-trained weights as the initialization transfers limited information and commits us to often massive pre-trained architectures. This procedure also precludes combining multiple pre-trained models that learn complementary information. To address these shortcomings, we introduce Adaptive Feature Transfer (AFT). Instead of transferring weights, AFT operates purely on features, thereby decoupling the choice of the pre-trained model from the smaller downstream model. Rather than indiscriminately compressing all pre-trained features, AFT adaptively transfers pre-trained features that are most useful for performing the downstream task, using a simple regularization that adds minimal overhead. Across multiple vision, language, and multi-modal datasets, AFT achieves significantly better downstream performance compared to alternatives with a similar computational cost. Furthermore, AFT reliably translates improvement in pre-trained models into improvement in downstream performance, even if the downstream model is over $50\times$ smaller, and can effectively transfer complementary information learned by multiple pre-trained models.

Using Uncertainty Quantification to Characterize and Improve Out-of-Domain Learning for PDEs

Existing work in scientific machine learning (SciML) has shown that data-driven learning of solution operators can provide a fast approximate alternative to classical numerical partial differential equation (PDE) solvers. Of these, Neural Operators (NOs) have emerged as particularly promising. We observe that several uncertainty quantification (UQ) methods for NOs fail for test inputs that are even moderately out-of-domain (OOD), even when the model approximates the solution well for in-domain tasks. To address this limitation, we show that ensembling several NOs can identify high-error regions and provide good uncertainty estimates that are well-correlated with prediction errors. Based on this, we propose a cost-effective alternative, DiverseNO, that mimics the properties of the ensemble by encouraging diverse predictions from its multiple heads in the last feed-forward layer. We then introduce Operator-ProbConserv, a method that uses these well-calibrated UQ estimates within the ProbConserv framework to update the model. Our empirical results show that Operator-ProbConserv enhances OOD model performance for a variety of challenging PDE problems and satisfies physical constraints such as conservation laws.

Chronos: Learning the Language of Time Series

We introduce Chronos, a simple yet effective framework for pretrained probabilistic time series models. Chronos tokenizes time series values using scaling and quantization into a fixed vocabulary and trains existing transformer-based language model architectures on these tokenized time series via the cross-entropy loss. We pretrained Chronos models based on the T5 family (ranging from 20M to 710M parameters) on a large collection of publicly available datasets, complemented by a synthetic dataset that we generated via Gaussian processes to improve generalization. In a comprehensive benchmark consisting of 42 datasets, and comprising both classical local models and deep learning methods, we show that Chronos models: (a) significantly outperform other methods on datasets that were part of the training corpus; and (b) have comparable and occasionally superior zero-shot performance on new datasets, relative to methods that were trained specifically on them. Our results demonstrate that Chronos models can leverage time series data from diverse domains to improve zero-shot accuracy on unseen forecasting tasks, positioning pretrained models as a viable tool to greatly simplify forecasting pipelines.