Using Uncertainty Quantification to Characterize and Improve Out-of-Domain Learning for PDEs

Existing work in scientific machine learning (SciML) has shown that data-driven learning of solution operators can provide a fast approximate alternative to classical numerical partial differential equation (PDE) solvers. Of these, Neural Operators (NOs) have emerged as particularly promising. We observe that several uncertainty quantification (UQ) methods for NOs fail for test inputs that are even moderately out-of-domain (OOD), even when the model approximates the solution well for in-domain tasks. To address this limitation, we show that ensembling several NOs can identify high-error regions and provide good uncertainty estimates that are well-correlated with prediction errors. Based on this, we propose a cost-effective alternative, DiverseNO, that mimics the properties of the ensemble by encouraging diverse predictions from its multiple heads in the last feed-forward layer. We then introduce Operator-ProbConserv, a method that uses these well-calibrated UQ estimates within the ProbConserv framework to update the model. Our empirical results show that Operator-ProbConserv enhances OOD model performance for a variety of challenging PDE problems and satisfies physical constraints such as conservation laws.

Pessimistic Off-Policy Multi-Objective Optimization

Multi-objective optimization is a type of decision making problems where multiple conflicting objectives are optimized. We study offline optimization of multi-objective policies from data collected by an existing policy. We propose a pessimistic estimator for the multi-objective policy values that can be easily plugged into existing formulas for hypervolume computation and optimized. The estimator is based on inverse propensity scores (IPS), and improves upon a naive IPS estimator in both theory and experiments. Our analysis is general, and applies beyond our IPS estimators and methods for optimizing them. The pessimistic estimator can be optimized by policy gradients and performs well in all of our experiments.

Learning Physical Models that Can Respect Conservation Laws

Recent work in scientific machine learning (SciML) has focused on incorporating partial differential equation (PDE) information into the learning process. Much of this work has focused on relatively ``easy'' PDE operators (e.g., elliptic and parabolic), with less emphasis on relatively ``hard'' PDE operators (e.g., hyperbolic). Within numerical PDEs, the latter problem class requires control of a type of volume element or conservation constraint, which is known to be challenging. Delivering on the promise of SciML requires seamlessly incorporating both types of problems into the learning process. To address this issue, we propose ProbConserv, a framework for incorporating conservation constraints into a generic SciML architecture. To do so, ProbConserv combines the integral form of a conservation law with a Bayesian update. We provide a detailed analysis of ProbConserv on learning with the Generalized Porous Medium Equation (GPME), a widely-applicable parameterized family of PDEs that illustrates the qualitative properties of both easier and harder PDEs. ProbConserv is effective for easy GPME variants, performing well with state-of-the-art competitors; and for harder GPME variants it outperforms other approaches that do not guarantee volume conservation. ProbConserv seamlessly enforces physical conservation constraints, maintains probabilistic uncertainty quantification (UQ), and deals well with shocks and heteroscedasticities. In each case, it achieves superior predictive performance on downstream tasks.

Guiding continuous operator learning through Physics-based boundary constraints

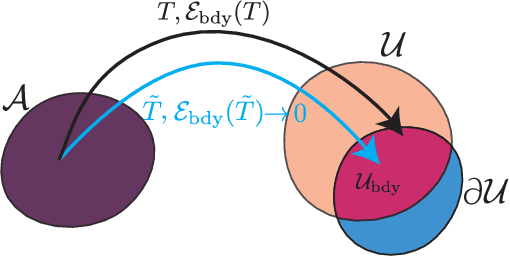
Boundary conditions (BCs) are important groups of physics-enforced constraints that are necessary for solutions of Partial Differential Equations (PDEs) to satisfy at specific spatial locations. These constraints carry important physical meaning, and guarantee the existence and the uniqueness of the PDE solution. Current neural-network based approaches that aim to solve PDEs rely only on training data to help the model learn BCs implicitly. There is no guarantee of BC satisfaction by these models during evaluation. In this work, we propose Boundary enforcing Operator Network (BOON) that enables the BC satisfaction of neural operators by making structural changes to the operator kernel. We provide our refinement procedure, and demonstrate the satisfaction of physics-based BCs, e.g. Dirichlet, Neumann, and periodic by the solutions obtained by BOON. Numerical experiments based on multiple PDEs with a wide variety of applications indicate that the proposed approach ensures satisfaction of BCs, and leads to more accurate solutions over the entire domain. The proposed correction method exhibits a (2X-20X) improvement over a given operator model in relative $L^2$ error (0.000084 relative $L^2$ error for Burgers' equation).

Convolutional Neural Networks for Facial Expression Recognition

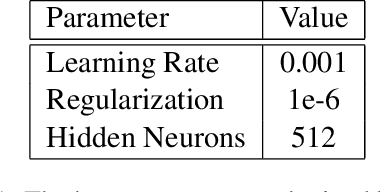
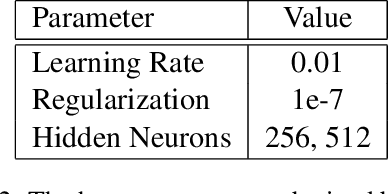
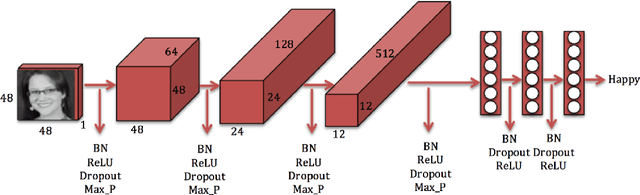
We have developed convolutional neural networks (CNN) for a facial expression recognition task. The goal is to classify each facial image into one of the seven facial emotion categories considered in this study. We trained CNN models with different depth using gray-scale images. We developed our models in Torch and exploited Graphics Processing Unit (GPU) computation in order to expedite the training process. In addition to the networks performing based on raw pixel data, we employed a hybrid feature strategy by which we trained a novel CNN model with the combination of raw pixel data and Histogram of Oriented Gradients (HOG) features. To reduce the overfitting of the models, we utilized different techniques including dropout and batch normalization in addition to L2 regularization. We applied cross validation to determine the optimal hyper-parameters and evaluated the performance of the developed models by looking at their training histories. We also present the visualization of different layers of a network to show what features of a face can be learned by CNN models.