Learning Probabilistic Filters with Strictly Proper Scoring Rules

Bayesian filtering of partially and noisily observed dynamical systems seeks to infer the evolving conditional distribution of the state of a dynamical system, given observations, in an online fashion. This Bayesian filtering distribution is the natural object for uncertainty quantification, but it is rarely available as a supervised learning target. However, one can often use the forecast model to generate synthetic system trajectories, along with synthetic observations. We introduce the proper scoring ensemble filter (PSEF), an ensemble data assimilation method based on training an analysis map to approximate the filtering distribution using only synthetic state--observation trajectories. The analysis step is represented as a permutation-invariant, transformer-based map that takes as input a forecast ensemble and observations, producing an analysis ensemble. Training is based on strictly proper scoring rules -- with the energy score used in our implementation -- so that probabilistic accuracy is rewarded over the whole probability distribution. We prove that, under a realizability assumption, the population objective is minimized by the true Bayesian filtering distribution. We also derive the finite-ensemble empirical objective used in training and relate its single state--observation trajectory form to the population objective, using a mean-field consistency argument. Numerical experiments show that the learned filter accurately approximates challenging filtering distributions, including nonlinear, non-Gaussian, and multi-modal posteriors, and achieves stronger performance in data assimilation tasks than classical methods or learning-based methods with mean-squared-error objectives. For close-to-Gaussian problems, learning a correction to the EnKF is the best approach, while for highly non-Gaussian problems an end-to-end approach that discards this inductive bias is superior.

Optimal Experimental Design for Reliable Learning of History-Dependent Constitutive Laws

History-dependent constitutive models serve as macroscopic closures for the aggregated effects of micromechanics. Their parameters are typically learned from experimental data. With a limited experimental budget, eliciting the full range of responses needed to characterize the constitutive relation can be difficult. As a result, the data can be well explained by a range of parameter choices, leading to parameter estimates that are uncertain or unreliable. To address this issue, we propose a Bayesian optimal experimental design framework to quantify, interpret, and maximize the utility of experimental designs for reliable learning of history-dependent constitutive models. In this framework, the design utility is defined as the expected reduction in parametric uncertainty or the expected information gain. This enables in silico design optimization using simulated data and reduces the cost of physical experiments for reliable parameter identification. We introduce two approximations that make this framework practical for advanced material testing with expensive forward models and high-dimensional data: (i) a Gaussian approximation of the expected information gain, and (ii) a surrogate approximation of the Fisher information matrix. The former enables efficient design optimization and interpretation, while the latter extends this approach to batched design optimization by amortizing the cost of repeated utility evaluations. Our numerical studies of uniaxial tests for viscoelastic solids show that optimized specimen geometries and loading paths yield image and force data that significantly improve parameter identifiability relative to random designs, especially for parameters associated with memory effects.

Large Language Models: A Mathematical Formulation

Large language models (LLMs) process and predict sequences containing text to answer questions, and address tasks including document summarization, providing recommendations, writing software and solving quantitative problems. We provide a mathematical framework for LLMs by describing the encoding of text sequences into sequences of tokens, defining the architecture for next-token prediction models, explaining how these models are learned from data, and demonstrating how they are deployed to address a variety of tasks. The mathematical sophistication required to understand this material is not high, and relies on straightforward ideas from information theory, probability and optimization. Nonetheless, the combination of ideas resting on these different components from the mathematical sciences yields a complex algorithmic structure; and this algorithmic structure has demonstrated remarkable empirical successes. The mathematical framework established here provides a platform from which it is possible to formulate and address questions concerning the accuracy, efficiency and robustness of the algorithms that constitute LLMs. The framework also suggests directions for development of modified and new methodologies.

Learning Enhanced Ensemble Filters

The filtering distribution in hidden Markov models evolves according to the law of a mean-field model in state--observation space. The ensemble Kalman filter (EnKF) approximates this mean-field model with an ensemble of interacting particles, employing a Gaussian ansatz for the joint distribution of the state and observation at each observation time. These methods are robust, but the Gaussian ansatz limits accuracy. This shortcoming is addressed by approximating the mean-field evolution using a novel form of neural operator taking probability distributions as input: a Measure Neural Mapping (MNM). A MNM is used to design a novel approach to filtering, the MNM-enhanced ensemble filter (MNMEF), which is defined in both the mean-fieldlimit and for interacting ensemble particle approximations. The ensemble approach uses empirical measures as input to the MNM and is implemented using the set transformer, which is invariant to ensemble permutation and allows for different ensemble sizes. The derivation of methods from a mean-field formulation allows a single parameterization of the algorithm to be deployed at different ensemble sizes. In practice fine-tuning of a small number of parameters, for specific ensemble sizes, further enhances the accuracy of the scheme. The promise of the approach is demonstrated by its superior root-mean-square-error performance relative to leading methods in filtering the Lorenz 96 and Kuramoto-Sivashinsky models.

Learning Memory and Material Dependent Constitutive Laws

The theory of homogenization provides a systematic approach to the derivation of macroscale constitutive laws, obviating the need to repeatedly resolve complex microstructure. However, the unit cell problem that defines the constitutive model is typically not amenable to explicit evaluation. It is therefore of interest to learn constitutive models from data generated by the unit cell problem. Many viscoelastic and elastoviscoplastic materials are characterized by memory-dependent constitutive laws. In order to amortize the computational investment in finding such memory-dependent constitutive laws, it is desirable to learn their dependence on the material microstructure. While prior work has addressed learning memory dependence and material dependence separately, their joint learning has not been considered. This paper focuses on the joint learning problem and proposes a novel neural operator framework to address it. In order to provide firm foundations, the homogenization problem for linear Kelvin-Voigt viscoelastic materials is studied. The theoretical properties of the cell problem in this Kelvin-Voigt setting are used to motivate the proposed general neural operator framework; these theoretical properties are also used to prove a universal approximation theorem for the learned macroscale constitutive model. This formulation of learnable constitutive models is then deployed beyond the Kelvin-Voigt setting. Numerical experiments are presented showing that the resulting data-driven methodology accurately learns history- and microstructure-dependent linear viscoelastic and nonlinear elastoviscoplastic constitutive models, and numerical results also demonstrate that the resulting constitutive models can be deployed in macroscale simulation of material deformation.

Hard Constraint Guided Flow Matching for Gradient-Free Generation of PDE Solutions

Generative models that satisfy hard constraints are crucial in many scientific and engineering applications where physical laws or system requirements must be strictly respected. However, many existing constrained generative models, especially those developed for computer vision, rely heavily on gradient information, often sparse or computationally expensive in fields like partial differential equations (PDEs). In this work, we introduce a novel framework for adapting pre-trained, unconstrained flow-matching models to satisfy constraints exactly in a zero-shot manner without requiring expensive gradient computations or fine-tuning. Our framework, ECI sampling, alternates between extrapolation (E), correction (C), and interpolation (I) stages during each iterative sampling step of flow matching sampling to ensure accurate integration of constraint information while preserving the validity of the generation. We demonstrate the effectiveness of our approach across various PDE systems, showing that ECI-guided generation strictly adheres to physical constraints and accurately captures complex distribution shifts induced by these constraints. Empirical results demonstrate that our framework consistently outperforms baseline approaches in various zero-shot constrained generation tasks and also achieves competitive results in the regression tasks without additional fine-tuning.

DreamBlend: Advancing Personalized Fine-tuning of Text-to-Image Diffusion Models

Given a small number of images of a subject, personalized image generation techniques can fine-tune large pre-trained text-to-image diffusion models to generate images of the subject in novel contexts, conditioned on text prompts. In doing so, a trade-off is made between prompt fidelity, subject fidelity and diversity. As the pre-trained model is fine-tuned, earlier checkpoints synthesize images with low subject fidelity but high prompt fidelity and diversity. In contrast, later checkpoints generate images with low prompt fidelity and diversity but high subject fidelity. This inherent trade-off limits the prompt fidelity, subject fidelity and diversity of generated images. In this work, we propose DreamBlend to combine the prompt fidelity from earlier checkpoints and the subject fidelity from later checkpoints during inference. We perform a cross attention guided image synthesis from a later checkpoint, guided by an image generated by an earlier checkpoint, for the same prompt. This enables generation of images with better subject fidelity, prompt fidelity and diversity on challenging prompts, outperforming state-of-the-art fine-tuning methods.

Inverse Problems and Data Assimilation: A Machine Learning Approach

The aim of these notes is to demonstrate the potential for ideas in machine learning to impact on the fields of inverse problems and data assimilation. The perspective is one that is primarily aimed at researchers from inverse problems and/or data assimilation who wish to see a mathematical presentation of machine learning as it pertains to their fields. As a by-product, we include a succinct mathematical treatment of various topics in machine learning.

Comparing and Contrasting Deep Learning Weather Prediction Backbones on Navier-Stokes and Atmospheric Dynamics

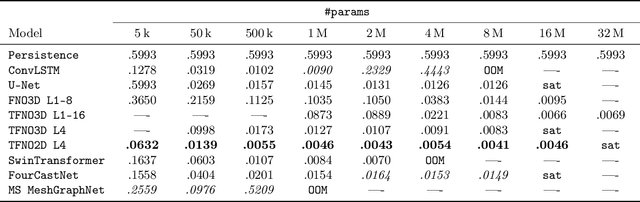
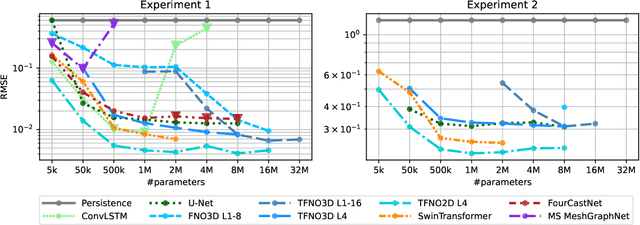
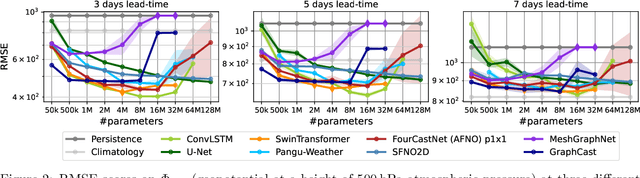
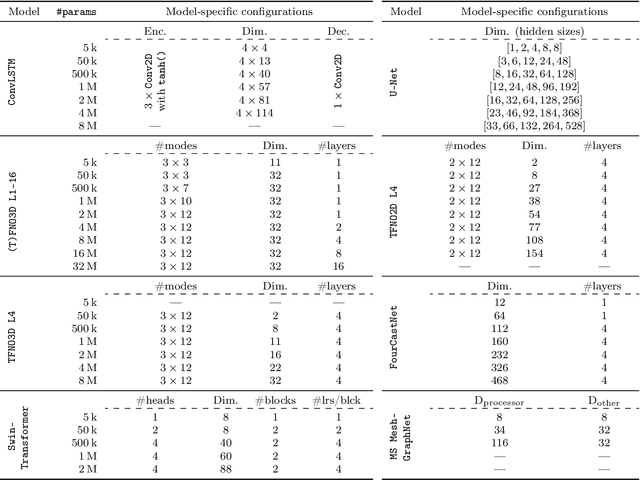
Remarkable progress in the development of Deep Learning Weather Prediction (DLWP) models positions them to become competitive with traditional numerical weather prediction (NWP) models. Indeed, a wide number of DLWP architectures -- based on various backbones, including U-Net, Transformer, Graph Neural Network (GNN), and Fourier Neural Operator (FNO) -- have demonstrated their potential at forecasting atmospheric states. However, due to differences in training protocols, forecast horizons, and data choices, it remains unclear which (if any) of these methods and architectures are most suitable for weather forecasting and for future model development. Here, we step back and provide a detailed empirical analysis, under controlled conditions, comparing and contrasting the most prominent DLWP models, along with their backbones. We accomplish this by predicting synthetic two-dimensional incompressible Navier-Stokes and real-world global weather dynamics. In terms of accuracy, memory consumption, and runtime, our results illustrate various tradeoffs. For example, on synthetic data, we observe favorable performance of FNO; and on the real-world WeatherBench dataset, our results demonstrate the suitability of ConvLSTM and SwinTransformer for short-to-mid-ranged forecasts. For long-ranged weather rollouts of up to 365 days, we observe superior stability and physical soundness in architectures that formulate a spherical data representation, i.e., GraphCast and Spherical FNO. In addition, we observe that all of these model backbones ``saturate,'' i.e., none of them exhibit so-called neural scaling, which highlights an important direction for future work on these and related models.

Learning Optimal Filters Using Variational Inference

Filtering-the task of estimating the conditional distribution of states of a dynamical system given partial, noisy, observations-is important in many areas of science and engineering, including weather and climate prediction. However, the filtering distribution is generally intractable to obtain for high-dimensional, nonlinear systems. Filters used in practice, such as the ensemble Kalman filter (EnKF), are biased for nonlinear systems and have numerous tuning parameters. Here, we present a framework for learning a parameterized analysis map-the map that takes a forecast distribution and observations to the filtering distribution-using variational inference. We show that this methodology can be used to learn gain matrices for filtering linear and nonlinear dynamical systems, as well as inflation and localization parameters for an EnKF. Future work will apply this framework to learn new filtering algorithms.