Learning Memory and Material Dependent Constitutive Laws

The theory of homogenization provides a systematic approach to the derivation of macroscale constitutive laws, obviating the need to repeatedly resolve complex microstructure. However, the unit cell problem that defines the constitutive model is typically not amenable to explicit evaluation. It is therefore of interest to learn constitutive models from data generated by the unit cell problem. Many viscoelastic and elastoviscoplastic materials are characterized by memory-dependent constitutive laws. In order to amortize the computational investment in finding such memory-dependent constitutive laws, it is desirable to learn their dependence on the material microstructure. While prior work has addressed learning memory dependence and material dependence separately, their joint learning has not been considered. This paper focuses on the joint learning problem and proposes a novel neural operator framework to address it. In order to provide firm foundations, the homogenization problem for linear Kelvin-Voigt viscoelastic materials is studied. The theoretical properties of the cell problem in this Kelvin-Voigt setting are used to motivate the proposed general neural operator framework; these theoretical properties are also used to prove a universal approximation theorem for the learned macroscale constitutive model. This formulation of learnable constitutive models is then deployed beyond the Kelvin-Voigt setting. Numerical experiments are presented showing that the resulting data-driven methodology accurately learns history- and microstructure-dependent linear viscoelastic and nonlinear elastoviscoplastic constitutive models, and numerical results also demonstrate that the resulting constitutive models can be deployed in macroscale simulation of material deformation.

Covariance alignment: from maximum likelihood estimation to Gromov-Wasserstein

Feature alignment methods are used in many scientific disciplines for data pooling, annotation, and comparison. As an instance of a permutation learning problem, feature alignment presents significant statistical and computational challenges. In this work, we propose the covariance alignment model to study and compare various alignment methods and establish a minimax lower bound for covariance alignment that has a non-standard dimension scaling because of the presence of a nuisance parameter. This lower bound is in fact minimax optimal and is achieved by a natural quasi MLE. However, this estimator involves a search over all permutations which is computationally infeasible even when the problem has moderate size. To overcome this limitation, we show that the celebrated Gromov-Wasserstein algorithm from optimal transport which is more amenable to fast implementation even on large-scale problems is also minimax optimal. These results give the first statistical justification for the deployment of the Gromov-Wasserstein algorithm in practice.

Optimal transport for automatic alignment of untargeted metabolomic data

Untargeted metabolomic profiling through liquid chromatography-mass spectrometry (LC-MS) measures a vast array of metabolites within biospecimens, advancing drug development, disease diagnosis, and risk prediction. However, the low throughput of LC-MS poses a major challenge for biomarker discovery, annotation, and experimental comparison, necessitating the merging of multiple datasets. Current data pooling methods encounter practical limitations due to their vulnerability to data variations and hyperparameter dependence. Here we introduce GromovMatcher, a flexible and user-friendly algorithm that automatically combines LC-MS datasets using optimal transport. By capitalizing on feature intensity correlation structures, GromovMatcher delivers superior alignment accuracy and robustness compared to existing approaches. This algorithm scales to thousands of features requiring minimal hyperparameter tuning. Applying our method to experimental patient studies of liver and pancreatic cancer, we discover shared metabolic features related to patient alcohol intake, demonstrating how GromovMatcher facilitates the search for biomarkers associated with lifestyle risk factors linked to several cancer types.

GULP: a prediction-based metric between representations

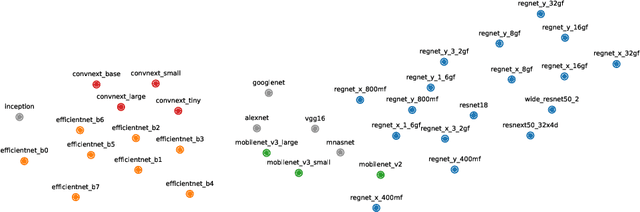
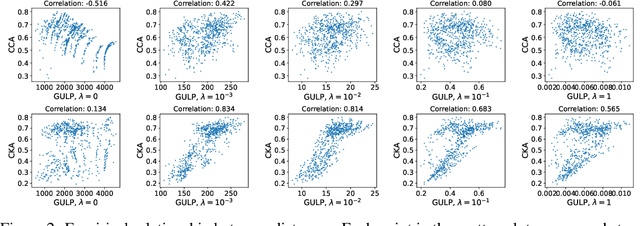
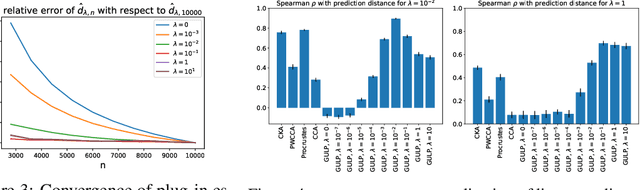
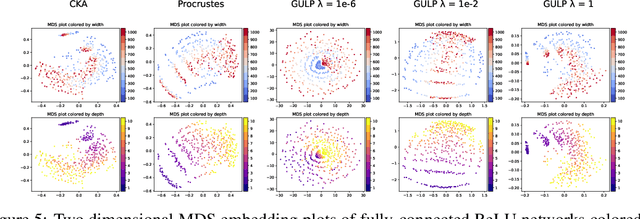
Comparing the representations learned by different neural networks has recently emerged as a key tool to understand various architectures and ultimately optimize them. In this work, we introduce GULP, a family of distance measures between representations that is explicitly motivated by downstream predictive tasks. By construction, GULP provides uniform control over the difference in prediction performance between two representations, with respect to regularized linear prediction tasks. Moreover, it satisfies several desirable structural properties, such as the triangle inequality and invariance under orthogonal transformations, and thus lends itself to data embedding and visualization. We extensively evaluate GULP relative to other methods, and demonstrate that it correctly differentiates between architecture families, converges over the course of training, and captures generalization performance on downstream linear tasks.