Learning Memory and Material Dependent Constitutive Laws

The theory of homogenization provides a systematic approach to the derivation of macroscale constitutive laws, obviating the need to repeatedly resolve complex microstructure. However, the unit cell problem that defines the constitutive model is typically not amenable to explicit evaluation. It is therefore of interest to learn constitutive models from data generated by the unit cell problem. Many viscoelastic and elastoviscoplastic materials are characterized by memory-dependent constitutive laws. In order to amortize the computational investment in finding such memory-dependent constitutive laws, it is desirable to learn their dependence on the material microstructure. While prior work has addressed learning memory dependence and material dependence separately, their joint learning has not been considered. This paper focuses on the joint learning problem and proposes a novel neural operator framework to address it. In order to provide firm foundations, the homogenization problem for linear Kelvin-Voigt viscoelastic materials is studied. The theoretical properties of the cell problem in this Kelvin-Voigt setting are used to motivate the proposed general neural operator framework; these theoretical properties are also used to prove a universal approximation theorem for the learned macroscale constitutive model. This formulation of learnable constitutive models is then deployed beyond the Kelvin-Voigt setting. Numerical experiments are presented showing that the resulting data-driven methodology accurately learns history- and microstructure-dependent linear viscoelastic and nonlinear elastoviscoplastic constitutive models, and numerical results also demonstrate that the resulting constitutive models can be deployed in macroscale simulation of material deformation.

Discretization Error of Fourier Neural Operators

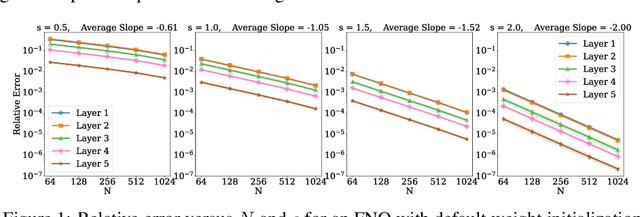
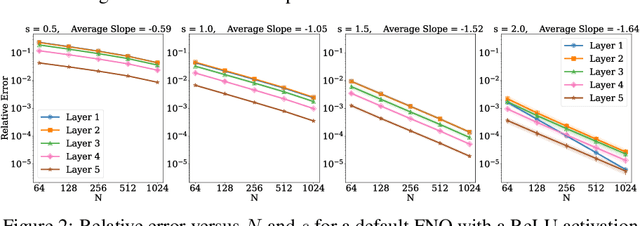
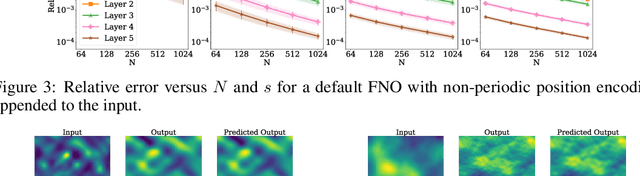
Operator learning is a variant of machine learning that is designed to approximate maps between function spaces from data. The Fourier Neural Operator (FNO) is a common model architecture used for operator learning. The FNO combines pointwise linear and nonlinear operations in physical space with pointwise linear operations in Fourier space, leading to a parameterized map acting between function spaces. Although FNOs formally involve convolutions of functions on a continuum, in practice the computations are performed on a discretized grid, allowing efficient implementation via the FFT. In this paper, the aliasing error that results from such a discretization is quantified and algebraic rates of convergence in terms of the grid resolution are obtained as a function of the regularity of the input. Numerical experiments that validate the theory and describe model stability are performed.

An operator learning perspective on parameter-to-observable maps

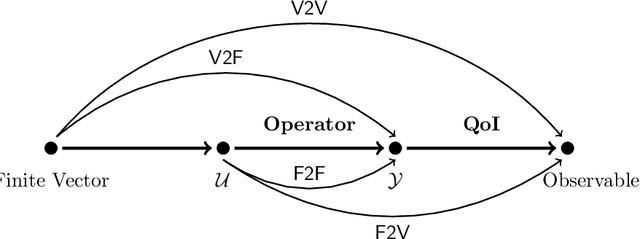
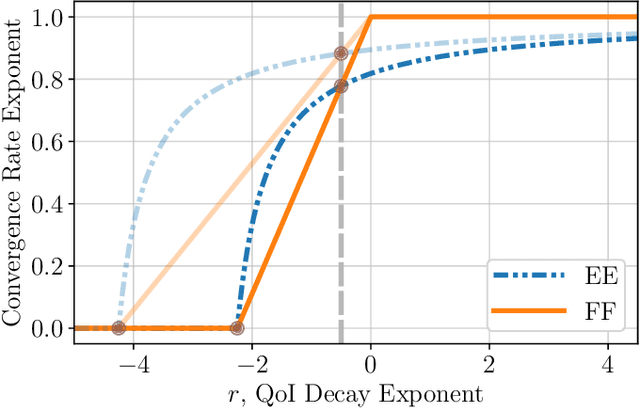
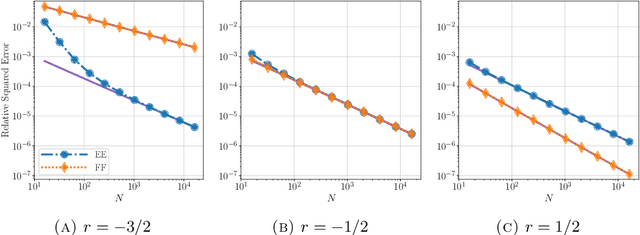
Computationally efficient surrogates for parametrized physical models play a crucial role in science and engineering. Operator learning provides data-driven surrogates that map between function spaces. However, instead of full-field measurements, often the available data are only finite-dimensional parametrizations of model inputs or finite observables of model outputs. Building off of Fourier Neural Operators, this paper introduces the Fourier Neural Mappings (FNMs) framework that is able to accommodate such finite-dimensional inputs and outputs. The paper develops universal approximation theorems for the method. Moreover, in many applications the underlying parameter-to-observable (PtO) map is defined implicitly through an infinite-dimensional operator, such as the solution operator of a partial differential equation. A natural question is whether it is more data-efficient to learn the PtO map end-to-end or first learn the solution operator and subsequently compute the observable from the full-field solution. A theoretical analysis of Bayesian nonparametric regression of linear functionals, which is of independent interest, suggests that the end-to-end approach can actually have worse sample complexity. Extending beyond the theory, numerical results for the FNM approximation of three nonlinear PtO maps demonstrate the benefits of the operator learning perspective that this paper adopts.

Learning Homogenization for Elliptic Operators

Multiscale partial differential equations (PDEs) arise in various applications, and several schemes have been developed to solve them efficiently. Homogenization theory is a powerful methodology that eliminates the small-scale dependence, resulting in simplified equations that are computationally tractable. In the field of continuum mechanics, homogenization is crucial for deriving constitutive laws that incorporate microscale physics in order to formulate balance laws for the macroscopic quantities of interest. However, obtaining homogenized constitutive laws is often challenging as they do not in general have an analytic form and can exhibit phenomena not present on the microscale. In response, data-driven learning of the constitutive law has been proposed as appropriate for this task. However, a major challenge in data-driven learning approaches for this problem has remained unexplored: the impact of discontinuities and corner interfaces in the underlying material. These discontinuities in the coefficients affect the smoothness of the solutions of the underlying equations. Given the prevalence of discontinuous materials in continuum mechanics applications, it is important to address the challenge of learning in this context; in particular to develop underpinning theory to establish the reliability of data-driven methods in this scientific domain. The paper addresses this unexplored challenge by investigating the learnability of homogenized constitutive laws for elliptic operators in the presence of such complexities. Approximation theory is presented, and numerical experiments are performed which validate the theory for the solution operator defined by the cell-problem arising in homogenization for elliptic PDEs.

Learn Like The Pro: Norms from Theory to Size Neural Computation

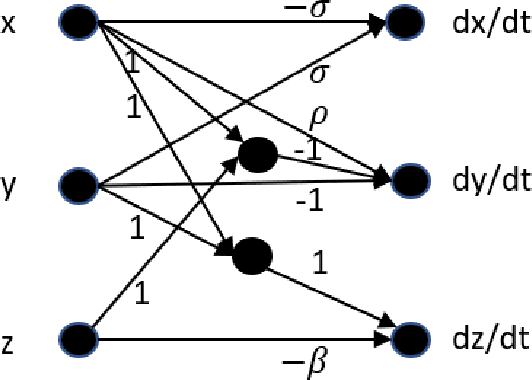
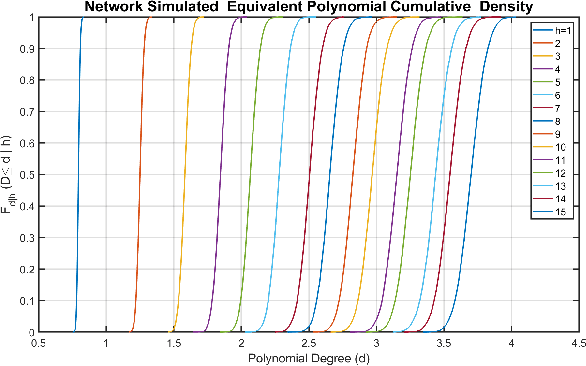
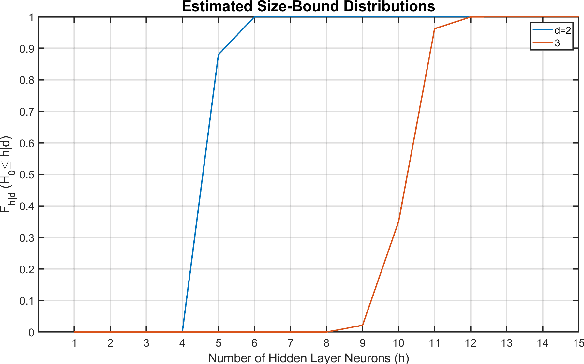
The optimal design of neural networks is a critical problem in many applications. Here, we investigate how dynamical systems with polynomial nonlinearities can inform the design of neural systems that seek to emulate them. We propose a Learnability metric and its associated features to quantify the near-equilibrium behavior of learning dynamics. Equating the Learnability of neural systems with equivalent parameter estimation metric of the reference system establishes bounds on network structure. In this way, norms from theory provide a good first guess for neural structure, which may then further adapt with data. The proposed approach neither requires training nor training data. It reveals exact sizing for a class of neural networks with multiplicative nodes that mimic continuous- or discrete-time polynomial dynamics. It also provides relatively tight lower size bounds for classical feed-forward networks that is consistent with simulated assessments.

Informative Neural Ensemble Kalman Learning

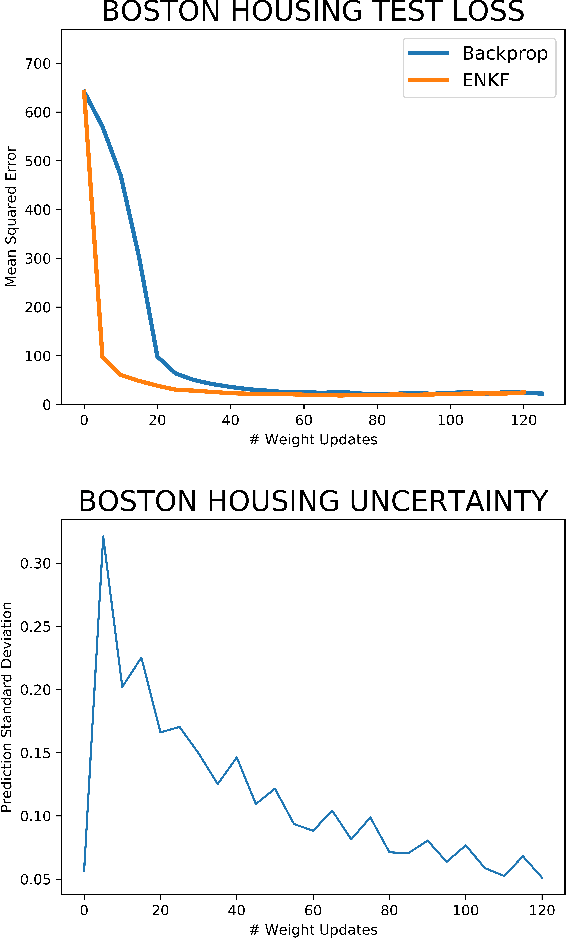
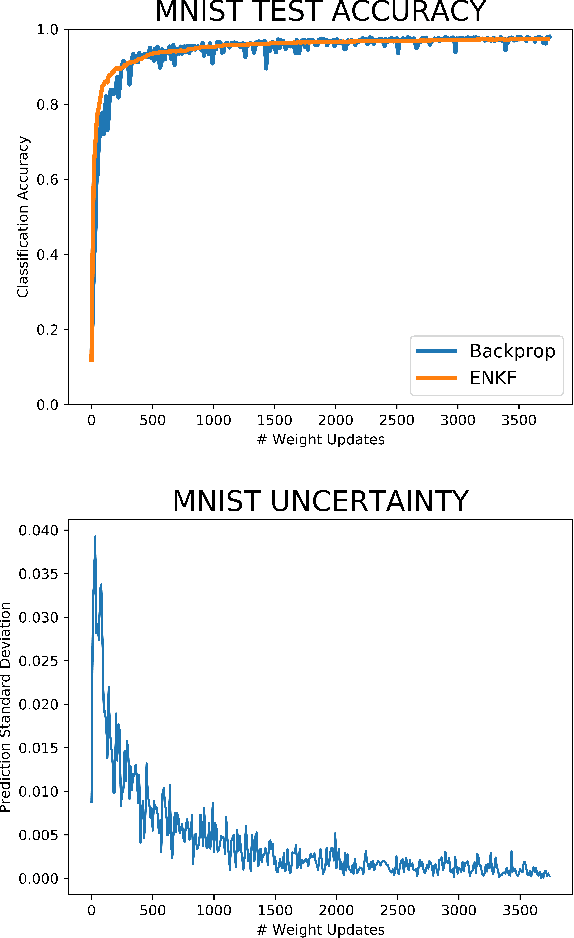
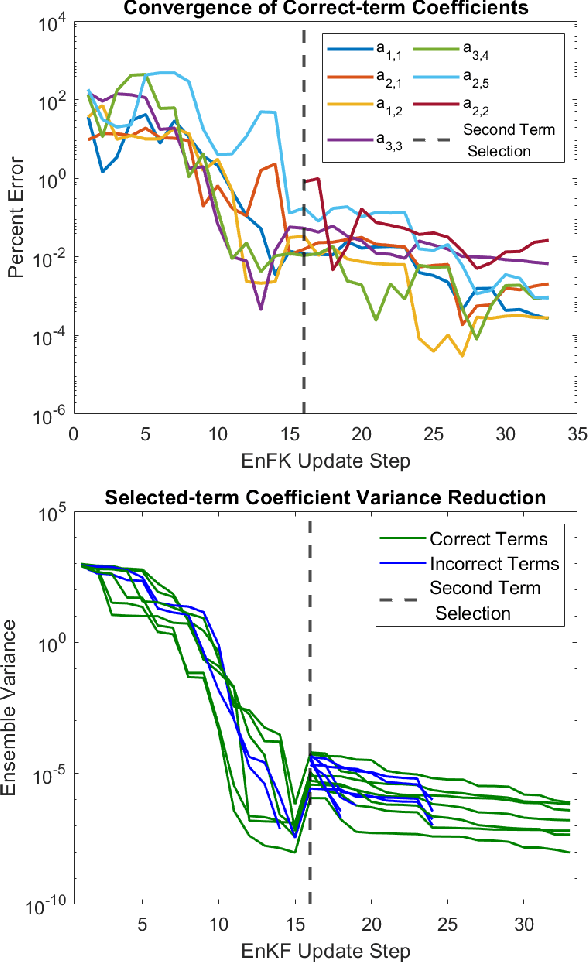
In stochastic systems, informative approaches select key measurement or decision variables that maximize information gain to enhance the efficacy of model-related inferences. Neural Learning also embodies stochastic dynamics, but informative Learning is less developed. Here, we propose Informative Ensemble Kalman Learning, which replaces backpropagation with an adaptive Ensemble Kalman Filter to quantify uncertainty and enables maximizing information gain during Learning. After demonstrating Ensemble Kalman Learning's competitive performance on standard datasets, we apply the informative approach to neural structure learning. In particular, we show that when trained from the Lorenz-63 system's simulations, the efficaciously learned structure recovers the dynamical equations. To the best of our knowledge, Informative Ensemble Kalman Learning is new. Results suggest that this approach to optimized Learning is promising.

Neural Integration of Continuous Dynamics

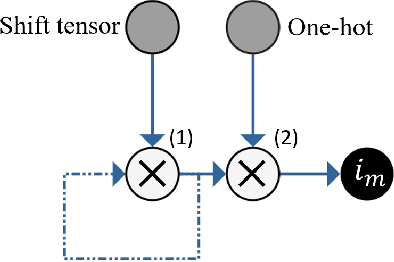
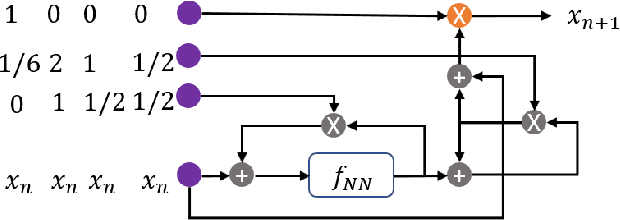
Neural dynamical systems are dynamical systems that are described at least in part by neural networks. The class of continuous-time neural dynamical systems must, however, be numerically integrated for simulation and learning. Here, we present a compact neural circuit for two common numerical integrators: the explicit fixed-step Runge-Kutta method of any order and the semi-implicit/predictor-corrector Adams-Bashforth-Moulton method. Modeled as constant-sized recurrent networks embedding a continuous neural differential equation, they achieve fully neural temporal output. Using the polynomial class of dynamical systems, we demonstrate the equivalence of neural and numerical integration.