Operator Learning Using Random Features: A Tool for Scientific Computing

Supervised operator learning centers on the use of training data, in the form of input-output pairs, to estimate maps between infinite-dimensional spaces. It is emerging as a powerful tool to complement traditional scientific computing, which may often be framed in terms of operators mapping between spaces of functions. Building on the classical random features methodology for scalar regression, this paper introduces the function-valued random features method. This leads to a supervised operator learning architecture that is practical for nonlinear problems yet is structured enough to facilitate efficient training through the optimization of a convex, quadratic cost. Due to the quadratic structure, the trained model is equipped with convergence guarantees and error and complexity bounds, properties that are not readily available for most other operator learning architectures. At its core, the proposed approach builds a linear combination of random operators. This turns out to be a low-rank approximation of an operator-valued kernel ridge regression algorithm, and hence the method also has strong connections to Gaussian process regression. The paper designs function-valued random features that are tailored to the structure of two nonlinear operator learning benchmark problems arising from parametric partial differential equations. Numerical results demonstrate the scalability, discretization invariance, and transferability of the function-valued random features method.

Hyperparameter Optimization for Randomized Algorithms: A Case Study for Random Features

Randomized algorithms exploit stochasticity to reduce computational complexity. One important example is random feature regression (RFR) that accelerates Gaussian process regression (GPR). RFR approximates an unknown function with a random neural network whose hidden weights and biases are sampled from a probability distribution. Only the final output layer is fit to data. In randomized algorithms like RFR, the hyperparameters that characterize the sampling distribution greatly impact performance, yet are not directly accessible from samples. This makes optimization of hyperparameters via standard (gradient-based) optimization tools inapplicable. Inspired by Bayesian ideas from GPR, this paper introduces a random objective function that is tailored for hyperparameter tuning of vector-valued random features. The objective is minimized with ensemble Kalman inversion (EKI). EKI is a gradient-free particle-based optimizer that is scalable to high-dimensions and robust to randomness in objective functions. A numerical study showcases the new black-box methodology to learn hyperparameter distributions in several problems that are sensitive to the hyperparameter selection: two global sensitivity analyses, integrating a chaotic dynamical system, and solving a Bayesian inverse problem from atmospheric dynamics. The success of the proposed EKI-based algorithm for RFR suggests its potential for automated optimization of hyperparameters arising in other randomized algorithms.

An operator learning perspective on parameter-to-observable maps

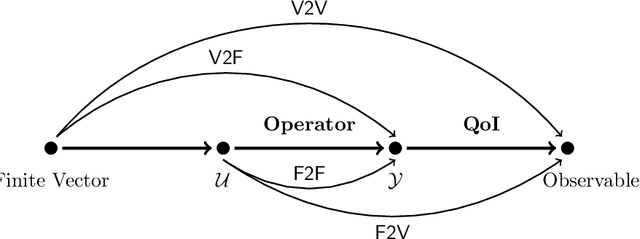
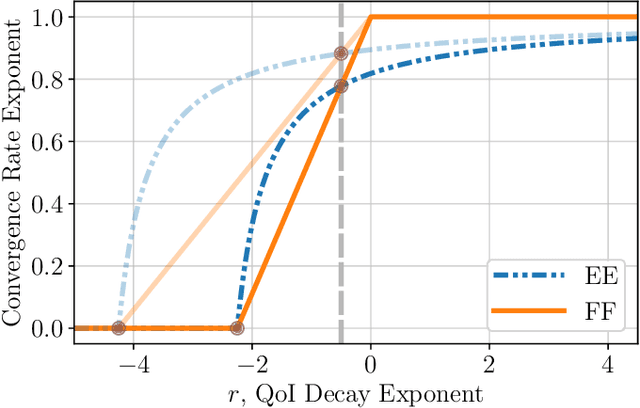
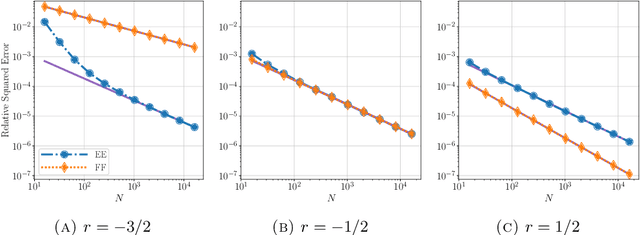
Computationally efficient surrogates for parametrized physical models play a crucial role in science and engineering. Operator learning provides data-driven surrogates that map between function spaces. However, instead of full-field measurements, often the available data are only finite-dimensional parametrizations of model inputs or finite observables of model outputs. Building off of Fourier Neural Operators, this paper introduces the Fourier Neural Mappings (FNMs) framework that is able to accommodate such finite-dimensional inputs and outputs. The paper develops universal approximation theorems for the method. Moreover, in many applications the underlying parameter-to-observable (PtO) map is defined implicitly through an infinite-dimensional operator, such as the solution operator of a partial differential equation. A natural question is whether it is more data-efficient to learn the PtO map end-to-end or first learn the solution operator and subsequently compute the observable from the full-field solution. A theoretical analysis of Bayesian nonparametric regression of linear functionals, which is of independent interest, suggests that the end-to-end approach can actually have worse sample complexity. Extending beyond the theory, numerical results for the FNM approximation of three nonlinear PtO maps demonstrate the benefits of the operator learning perspective that this paper adopts.

Error Bounds for Learning with Vector-Valued Random Features

This paper provides a comprehensive error analysis of learning with vector-valued random features (RF). The theory is developed for RF ridge regression in a fully general infinite-dimensional input-output setting, but nonetheless applies to and improves existing finite-dimensional analyses. In contrast to comparable work in the literature, the approach proposed here relies on a direct analysis of the underlying risk functional and completely avoids the explicit RF ridge regression solution formula in terms of random matrices. This removes the need for concentration results in random matrix theory or their generalizations to random operators. The main results established in this paper include strong consistency of vector-valued RF estimators under model misspecification and minimax optimal convergence rates in the well-specified setting. The parameter complexity (number of random features) and sample complexity (number of labeled data) required to achieve such rates are comparable with Monte Carlo intuition and free from logarithmic factors.

Convergence Rates for Learning Linear Operators from Noisy Data

We study the Bayesian inverse problem of learning a linear operator on a Hilbert space from its noisy pointwise evaluations on random input data. Our framework assumes that this target operator is self-adjoint and diagonal in a basis shared with the Gaussian prior and noise covariance operators arising from the imposed statistical model and is able to handle target operators that are compact, bounded, or even unbounded. We establish posterior contraction rates with respect to a family of Bochner norms as the number of data tend to infinity and derive related lower bounds on the estimation error. In the large data limit, we also provide asymptotic convergence rates of suitably defined excess risk and generalization gap functionals associated with the posterior mean point estimator. In doing so, we connect the posterior consistency results to nonparametric learning theory. Furthermore, these convergence rates highlight and quantify the difficulty of learning unbounded linear operators in comparison with the learning of bounded or compact ones. Numerical experiments confirm the theory and demonstrate that similar conclusions may be expected in more general problem settings.

The Random Feature Model for Input-Output Maps between Banach Spaces

Well known to the machine learning community, the random feature model, originally introduced by Rahimi and Recht in 2008, is a parametric approximation to kernel interpolation or regression methods. It is typically used to approximate functions mapping a finite-dimensional input space to the real line. In this paper, we instead propose a methodology for use of the random feature model as a data-driven surrogate for operators that map an input Banach space to an output Banach space. Although the methodology is quite general, we consider operators defined by partial differential equations (PDEs); here, the inputs and outputs are themselves functions, with the input parameters being functions required to specify the problem, such as initial data or coefficients, and the outputs being solutions of the problem. Upon discretization, the model inherits several desirable attributes from this infinite-dimensional, function space viewpoint, including mesh-invariant approximation error with respect to the true PDE solution map and the capability to be trained at one mesh resolution and then deployed at different mesh resolutions. We view the random feature model as a non-intrusive data-driven emulator, provide a mathematical framework for its interpretation, and demonstrate its ability to efficiently and accurately approximate the nonlinear parameter-to-solution maps of two prototypical PDEs arising in physical science and engineering applications: viscous Burgers' equation and a variable coefficient elliptic equation.