Continuum Attention for Neural Operators

Transformers, and the attention mechanism in particular, have become ubiquitous in machine learning. Their success in modeling nonlocal, long-range correlations has led to their widespread adoption in natural language processing, computer vision, and time-series problems. Neural operators, which map spaces of functions into spaces of functions, are necessarily both nonlinear and nonlocal if they are universal; it is thus natural to ask whether the attention mechanism can be used in the design of neural operators. Motivated by this, we study transformers in the function space setting. We formulate attention as a map between infinite dimensional function spaces and prove that the attention mechanism as implemented in practice is a Monte Carlo or finite difference approximation of this operator. The function space formulation allows for the design of transformer neural operators, a class of architectures designed to learn mappings between function spaces, for which we prove a universal approximation result. The prohibitive cost of applying the attention operator to functions defined on multi-dimensional domains leads to the need for more efficient attention-based architectures. For this reason we also introduce a function space generalization of the patching strategy from computer vision, and introduce a class of associated neural operators. Numerical results, on an array of operator learning problems, demonstrate the promise of our approaches to function space formulations of attention and their use in neural operators.

Data Complexity Estimates for Operator Learning

Operator learning has emerged as a new paradigm for the data-driven approximation of nonlinear operators. Despite its empirical success, the theoretical underpinnings governing the conditions for efficient operator learning remain incomplete. The present work develops theory to study the data complexity of operator learning, complementing existing research on the parametric complexity. We investigate the fundamental question: How many input/output samples are needed in operator learning to achieve a desired accuracy $\epsilon$? This question is addressed from the point of view of $n$-widths, and this work makes two key contributions. The first contribution is to derive lower bounds on $n$-widths for general classes of Lipschitz and Fr\'echet differentiable operators. These bounds rigorously demonstrate a ``curse of data-complexity'', revealing that learning on such general classes requires a sample size exponential in the inverse of the desired accuracy $\epsilon$. The second contribution of this work is to show that ``parametric efficiency'' implies ``data efficiency''; using the Fourier neural operator (FNO) as a case study, we show rigorously that on a narrower class of operators, efficiently approximated by FNO in terms of the number of tunable parameters, efficient operator learning is attainable in data complexity as well. Specifically, we show that if only an algebraically increasing number of tunable parameters is needed to reach a desired approximation accuracy, then an algebraically bounded number of data samples is also sufficient to achieve the same accuracy.

Operator Learning: Algorithms and Analysis

Operator learning refers to the application of ideas from machine learning to approximate (typically nonlinear) operators mapping between Banach spaces of functions. Such operators often arise from physical models expressed in terms of partial differential equations (PDEs). In this context, such approximate operators hold great potential as efficient surrogate models to complement traditional numerical methods in many-query tasks. Being data-driven, they also enable model discovery when a mathematical description in terms of a PDE is not available. This review focuses primarily on neural operators, built on the success of deep neural networks in the approximation of functions defined on finite dimensional Euclidean spaces. Empirically, neural operators have shown success in a variety of applications, but our theoretical understanding remains incomplete. This review article summarizes recent progress and the current state of our theoretical understanding of neural operators, focusing on an approximation theoretic point of view.

Score-based Diffusion Models in Function Space

Diffusion models have recently emerged as a powerful framework for generative modeling. They consist of a forward process that perturbs input data with Gaussian white noise and a reverse process that learns a score function to generate samples by denoising. Despite their tremendous success, they are mostly formulated on finite-dimensional spaces, e.g. Euclidean, limiting their applications to many domains where the data has a functional form such as in scientific computing and 3D geometric data analysis. In this work, we introduce a mathematically rigorous framework called Denoising Diffusion Operators (DDOs) for training diffusion models in function space. In DDOs, the forward process perturbs input functions gradually using a Gaussian process. The generative process is formulated by integrating a function-valued Langevin dynamic. Our approach requires an appropriate notion of the score for the perturbed data distribution, which we obtain by generalizing denoising score matching to function spaces that can be infinite-dimensional. We show that the corresponding discretized algorithm generates accurate samples at a fixed cost that is independent of the data resolution. We theoretically and numerically verify the applicability of our approach on a set of problems, including generating solutions to the Navier-Stokes equation viewed as the push-forward distribution of forcings from a Gaussian Random Field (GRF).

Convergence Rates for Learning Linear Operators from Noisy Data

We study the Bayesian inverse problem of learning a linear operator on a Hilbert space from its noisy pointwise evaluations on random input data. Our framework assumes that this target operator is self-adjoint and diagonal in a basis shared with the Gaussian prior and noise covariance operators arising from the imposed statistical model and is able to handle target operators that are compact, bounded, or even unbounded. We establish posterior contraction rates with respect to a family of Bochner norms as the number of data tend to infinity and derive related lower bounds on the estimation error. In the large data limit, we also provide asymptotic convergence rates of suitably defined excess risk and generalization gap functionals associated with the posterior mean point estimator. In doing so, we connect the posterior consistency results to nonparametric learning theory. Furthermore, these convergence rates highlight and quantify the difficulty of learning unbounded linear operators in comparison with the learning of bounded or compact ones. Numerical experiments confirm the theory and demonstrate that similar conclusions may be expected in more general problem settings.

Model Reduction and Neural Networks for Parametric PDEs

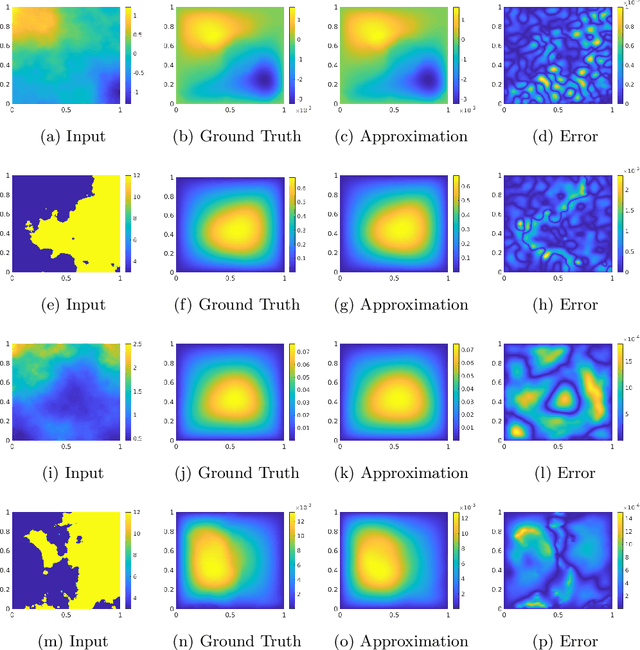
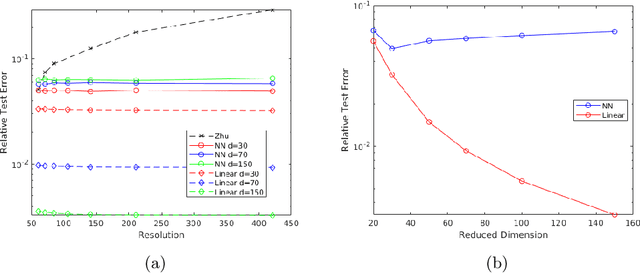
We develop a general framework for data-driven approximation of input-output maps between infinite-dimensional spaces. The proposed approach is motivated by the recent successes of neural networks and deep learning, in combination with ideas from model reduction. This combination results in a neural network approximation which, in principle, is defined on infinite-dimensional spaces and, in practice, is robust to the dimension of finite-dimensional approximations of these spaces required for computation. For a class of input-output maps, and suitably chosen probability measures on the inputs, we prove convergence of the proposed approximation methodology. Numerically we demonstrate the effectiveness of the method on a class of parametric elliptic PDE problems, showing convergence and robustness of the approximation scheme with respect to the size of the discretization, and compare our method with existing algorithms from the literature.

Regression-clustering for Improved Accuracy and Training Cost with Molecular-Orbital-Based Machine Learning

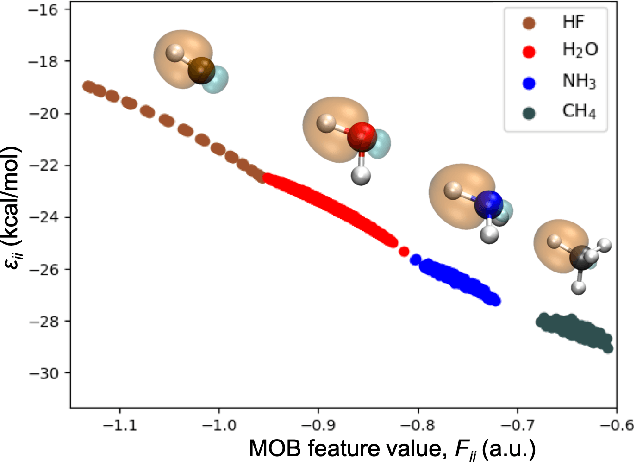
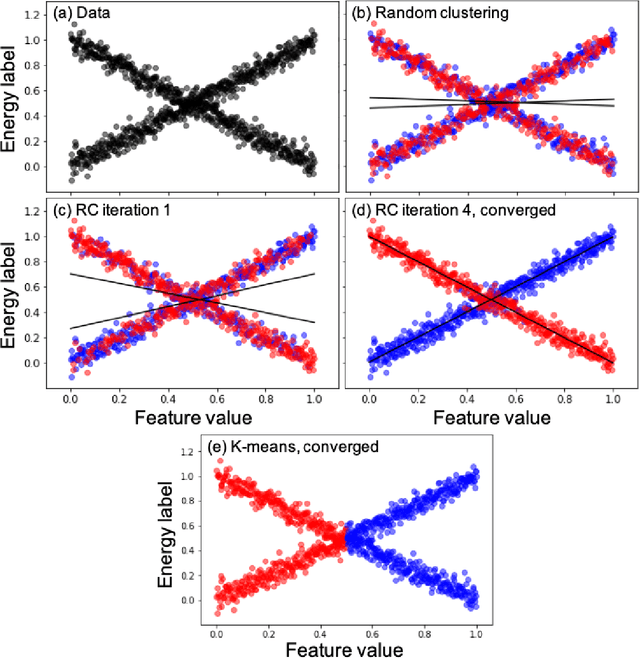
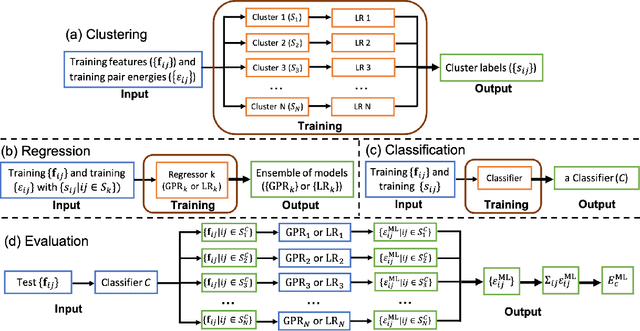
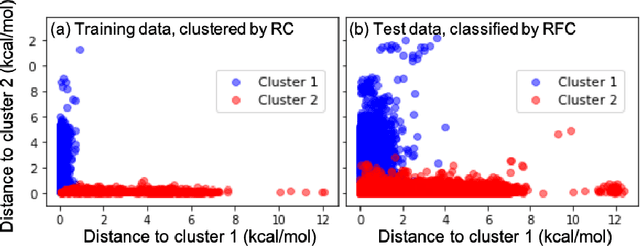
Machine learning (ML) in the representation of molecular-orbital-based (MOB) features has been shown to be an accurate and transferable approach to the prediction of post-Hartree-Fock correlation energies. Previous applications of MOB-ML employed Gaussian Process Regression (GPR), which provides good prediction accuracy with small training sets; however, the cost of GPR training scales cubically with the amount of data and becomes a computational bottleneck for large training sets. In the current work, we address this problem by introducing a clustering/regression/classification implementation of MOB-ML. In a first step, regression clustering (RC) is used to partition the training data to best fit an ensemble of linear regression (LR) models; in a second step, each cluster is regressed independently, using either LR or GPR; and in a third step, a random forest classifier (RFC) is trained for the prediction of cluster assignments based on MOB feature values. Upon inspection, RC is found to recapitulate chemically intuitive groupings of the frontier molecular orbitals, and the combined RC/LR/RFC and RC/GPR/RFC implementations of MOB-ML are found to provide good prediction accuracy with greatly reduced wall-clock training times. For a dataset of thermalized geometries of 7211 organic molecules of up to seven heavy atoms, both implementations reach chemical accuracy (1 kcal/mol error) with only 300 training molecules, while providing 35000-fold and 4500-fold reductions in the wall-clock training time, respectively, compared to MOB-ML without clustering. The resulting models are also demonstrated to retain transferability for the prediction of large-molecule energies with only small-molecule training data. Finally, it is shown that capping the number of training datapoints per cluster leads to further improvements in prediction accuracy with negligible increases in wall-clock training time.

Analysis Of Momentum Methods

Gradient decent-based optimization methods underpin the parameter training which results in the impressive results now found when testing neural networks. Introducing stochasticity is key to their success in practical problems, and there is some understanding of the role of stochastic gradient decent in this context. Momentum modifications of gradient decent such as Polyak's Heavy Ball method (HB) and Nesterov's method of accelerated gradients (NAG), are widely adopted. In this work, our focus is on understanding the role of momentum in the training of neural networks, concentrating on the common situation in which the momentum contribution is fixed at each step of the algorithm; to expose the ideas simply we work in the deterministic setting. We show that, contrary to popular belief, standard implementations of fixed momentum methods do no more than act to rescale the learning rate. We achieve this by showing that the momentum method converges to a gradient flow, with a momentum-dependent time-rescaling, using the method of modified equations from numerical analysis. Further we show that the momentum method admits an exponentially attractive invariant manifold on which the dynamic reduces to a gradient flow with respect to a modified loss function, equal to the original one plus a small perturbation.

Ensemble Kalman Inversion: A Derivative-Free Technique For Machine Learning Tasks

The standard probabilistic perspective on machine learning gives rise to empirical risk-minimization tasks that are frequently solved by stochastic gradient descent (SGD) and variants thereof. We present a formulation of these tasks as classical inverse or filtering problems and, furthermore, we propose an efficient, gradient-free algorithm for finding a solution to these problems using ensemble Kalman inversion (EKI). Applications of our approach include offline and online supervised learning with deep neural networks, as well as graph-based semi-supervised learning. The essence of the EKI procedure is an ensemble based approximate gradient descent in which derivatives are replaced by differences from within the ensemble. We suggest several modifications to the basic method, derived from empirically successful heuristics developed in the context of SGD. Numerical results demonstrate wide applicability and robustness of the proposed algorithm.