Error Analysis of Bayesian Inverse Problems with Generative Priors

Data-driven methods for the solution of inverse problems have become widely popular in recent years thanks to the rise of machine learning techniques. A popular approach concerns the training of a generative model on additional data to learn a bespoke prior for the problem at hand. In this article we present an analysis for such problems by presenting quantitative error bounds for minimum Wasserstein-2 generative models for the prior. We show that under some assumptions, the error in the posterior due to the generative prior will inherit the same rate as the prior with respect to the Wasserstein-1 distance. We further present numerical experiments that verify that aspects of our error analysis manifests in some benchmarks followed by an elliptic PDE inverse problem where a generative prior is used to model a non-stationary field.

Physics-Informed Neural Networks for Source Inversion and Parameters Estimation in Atmospheric Dispersion

Recent studies have shown the success of deep learning in solving forward and inverse problems in engineering and scientific computing domains, such as physics-informed neural networks (PINNs). In the fields of atmospheric science and environmental monitoring, estimating emission source locations is a central task that further relies on multiple model parameters that dictate velocity profiles and diffusion parameters. Estimating these parameters at the same time as emission sources from scarce data is a difficult task. In this work, we achieve this by leveraging the flexibility and generality of PINNs. We use a weighted adaptive method based on the neural tangent kernels to solve a source inversion problem with parameter estimation on the 2D and 3D advection-diffusion equations with unknown velocity and diffusion coefficients that may vary in space and time. Our proposed weighted adaptive method is presented as an extension of PINNs for forward PDE problems to a highly ill-posed source inversion and parameter estimation problem. The key idea behind our methodology is to attempt the joint recovery of the solution, the sources along with the unknown parameters, thereby using the underlying partial differential equation as a constraint that couples multiple unknown functional parameters, leading to more efficient use of the limited information in the measurements. We present various numerical experiments, using different types of measurements that model practical engineering systems, to show that our proposed method is indeed successful and robust to additional noise in the measurements.

Learning Paths for Dynamic Measure Transport: A Control Perspective

We bring a control perspective to the problem of identifying paths of measures for sampling via dynamic measure transport (DMT). We highlight the fact that commonly used paths may be poor choices for DMT and connect existing methods for learning alternate paths to mean-field games. Based on these connections we pose a flexible family of optimization problems for identifying tilted paths of measures for DMT and advocate for the use of objective terms which encourage smoothness of the corresponding velocities. We present a numerical algorithm for solving these problems based on recent Gaussian process methods for solution of partial differential equations and demonstrate the ability of our method to recover more efficient and smooth transport models compared to those which use an untilted reference path.

Error Analysis of Triangular Optimal Transport Maps for Filtering

We present a systematic analysis of estimation errors for a class of optimal transport based algorithms for filtering and data assimilation. Along the way, we extend previous error analyses of Brenier maps to the case of conditional Brenier maps that arise in the context of simulation based inference. We then apply these results in a filtering scenario to analyze the optimal transport filtering algorithm of Al-Jarrah et al. (2024, ICML). An extension of that algorithm along with numerical benchmarks on various non-Gaussian and high-dimensional examples are provided to demonstrate its effectiveness and practical potential.

Score-Based Deterministic Density Sampling

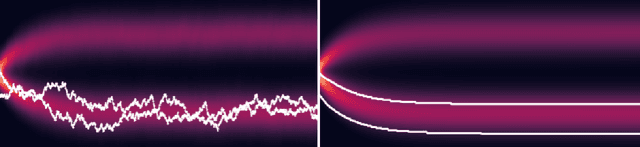
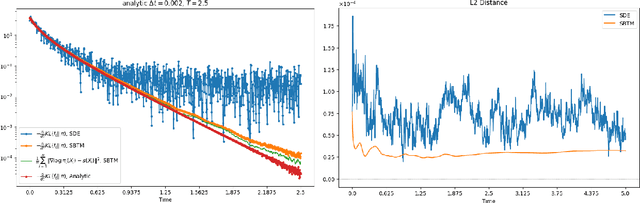
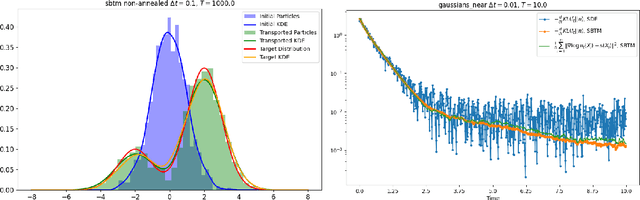
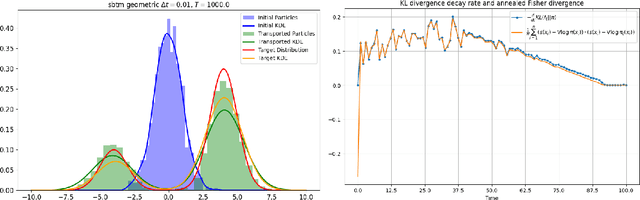
We propose and analyze a deterministic sampling framework using Score-Based Transport Modeling (SBTM) for sampling an unnormalized target density $\pi$. While diffusion generative modeling relies on pre-training the score function $\nabla \log f_t$ using samples from $\pi$, SBTM addresses the more general and challenging setting where only $\nabla \log\pi$ is known. SBTM approximates the Wasserstein gradient flow on KL$(f_t\|\pi)$ by learning the time-varying score $\nabla \log f_t$ on the fly using score matching. The learned score gives immediate access to relative Fisher information, providing a built-in convergence diagnostic. The deterministic trajectories are smooth, interpretable, and free of Brownian-motion noise, while having the same distribution as ULA. We prove that SBTM dissipates relative entropy at the same rate as the exact gradient flow, provided sufficient training. We further extend our framework to annealed dynamics, to handle non log-concave targets. Numerical experiments validate our theoretical findings: SBTM converges at the optimal rate, has smooth trajectories, and is easily integrated with annealed dynamics. We compare to the baselines of ULA and annealed ULA.

Fast filtering of non-Gaussian models using Amortized Optimal Transport Maps

In this paper, we present the amortized optimal transport filter (A-OTF) designed to mitigate the computational burden associated with the real-time training of optimal transport filters (OTFs). OTFs can perform accurate non-Gaussian Bayesian updates in the filtering procedure, but they require training at every time step, which makes them expensive. The proposed A-OTF framework exploits the similarity between OTF maps during an initial/offline training stage in order to reduce the cost of inference during online calculations. More precisely, we use clustering algorithms to select relevant subsets of pre-trained maps whose weighted average is used to compute the A-OTF model akin to a mixture of experts. A series of numerical experiments validate that A-OTF achieves substantial computational savings during online inference while preserving the inherent flexibility and accuracy of OTF.

Data-Efficient Kernel Methods for Learning Differential Equations and Their Solution Operators: Algorithms and Error Analysis

We introduce a novel kernel-based framework for learning differential equations and their solution maps that is efficient in data requirements, in terms of solution examples and amount of measurements from each example, and computational cost, in terms of training procedures. Our approach is mathematically interpretable and backed by rigorous theoretical guarantees in the form of quantitative worst-case error bounds for the learned equation. Numerical benchmarks demonstrate significant improvements in computational complexity and robustness while achieving one to two orders of magnitude improvements in terms of accuracy compared to state-of-the-art algorithms.

Gaussian Measures Conditioned on Nonlinear Observations: Consistency, MAP Estimators, and Simulation

The article presents a systematic study of the problem of conditioning a Gaussian random variable $\xi$ on nonlinear observations of the form $F \circ \phi(\xi)$ where $\phi: \mathcal{X} \to \mathbb{R}^N$ is a bounded linear operator and $F$ is nonlinear. Such problems arise in the context of Bayesian inference and recent machine learning-inspired PDE solvers. We give a representer theorem for the conditioned random variable $\xi \mid F\circ \phi(\xi)$, stating that it decomposes as the sum of an infinite-dimensional Gaussian (which is identified analytically) as well as a finite-dimensional non-Gaussian measure. We also introduce a novel notion of the mode of a conditional measure by taking the limit of the natural relaxation of the problem, to which we can apply the existing notion of maximum a posteriori estimators of posterior measures. Finally, we introduce a variant of the Laplace approximation for the efficient simulation of the aforementioned conditioned Gaussian random variables towards uncertainty quantification.

Diffeomorphic Measure Matching with Kernels for Generative Modeling

This article presents a general framework for the transport of probability measures towards minimum divergence generative modeling and sampling using ordinary differential equations (ODEs) and Reproducing Kernel Hilbert Spaces (RKHSs), inspired by ideas from diffeomorphic matching and image registration. A theoretical analysis of the proposed method is presented, giving a priori error bounds in terms of the complexity of the model, the number of samples in the training set, and model misspecification. An extensive suite of numerical experiments further highlights the properties, strengths, and weaknesses of the method and extends its applicability to other tasks, such as conditional simulation and inference.

Conditional Optimal Transport on Function Spaces

We present a systematic study of conditional triangular transport maps in function spaces from the perspective of optimal transportation and with a view towards amortized Bayesian inference. More specifically, we develop a theory of constrained optimal transport problems that describe block-triangular Monge maps that characterize conditional measures along with their Kantorovich relaxations. This generalizes the theory of optimal triangular transport to separable infinite-dimensional function spaces with general cost functions. We further tailor our results to the case of Bayesian inference problems and obtain regularity estimates on the conditioning maps from the prior to the posterior. Finally, we present numerical experiments that demonstrate the computational applicability of our theoretical results for amortized and likelihood-free inference of functional parameters.