Reducing the cost of posterior sampling in linear inverse problems via task-dependent score learning

Score-based diffusion models (SDMs) offer a flexible approach to sample from the posterior distribution in a variety of Bayesian inverse problems. In the literature, the prior score is utilized to sample from the posterior by different methods that require multiple evaluations of the forward mapping in order to generate a single posterior sample. These methods are often designed with the objective of enabling the direct use of the unconditional prior score and, therefore, task-independent training. In this paper, we focus on linear inverse problems, when evaluation of the forward mapping is computationally expensive and frequent posterior sampling is required for new measurement data, such as in medical imaging. We demonstrate that the evaluation of the forward mapping can be entirely bypassed during posterior sample generation. Instead, without introducing any error, the computational effort can be shifted to an offline task of training the score of a specific diffusion-like random process. In particular, the training is task-dependent requiring information about the forward mapping but not about the measurement data. It is shown that the conditional score corresponding to the posterior can be obtained from the auxiliary score by suitable affine transformations. We prove that this observation generalizes to the framework of infinite-dimensional diffusion models introduced recently and provide numerical analysis of the method. Moreover, we validate our findings with numerical experiments.

Laboratory Experiments of Model-based Reinforcement Learning for Adaptive Optics Control

Direct imaging of Earth-like exoplanets is one of the most prominent scientific drivers of the next generation of ground-based telescopes. Typically, Earth-like exoplanets are located at small angular separations from their host stars, making their detection difficult. Consequently, the adaptive optics (AO) system's control algorithm must be carefully designed to distinguish the exoplanet from the residual light produced by the host star. A new promising avenue of research to improve AO control builds on data-driven control methods such as Reinforcement Learning (RL). RL is an active branch of the machine learning research field, where control of a system is learned through interaction with the environment. Thus, RL can be seen as an automated approach to AO control, where its usage is entirely a turnkey operation. In particular, model-based reinforcement learning (MBRL) has been shown to cope with both temporal and misregistration errors. Similarly, it has been demonstrated to adapt to non-linear wavefront sensing while being efficient in training and execution. In this work, we implement and adapt an RL method called Policy Optimization for AO (PO4AO) to the GHOST test bench at ESO headquarters, where we demonstrate a strong performance of the method in a laboratory environment. Our implementation allows the training to be performed parallel to inference, which is crucial for on-sky operation. In particular, we study the predictive and self-calibrating aspects of the method. The new implementation on GHOST running PyTorch introduces only around 700 microseconds in addition to hardware, pipeline, and Python interface latency. We open-source well-documented code for the implementation and specify the requirements for the RTC pipeline. We also discuss the important hyperparameters of the method, the source of the latency, and the possible paths for a lower latency implementation.

Statistical inverse learning problems with random observations

We provide an overview of recent progress in statistical inverse problems with random experimental design, covering both linear and nonlinear inverse problems. Different regularization schemes have been studied to produce robust and stable solutions. We discuss recent results in spectral regularization methods and regularization by projection, exploring both approaches within the context of Hilbert scales and presenting new insights particularly in regularization by projection. Additionally, we overview recent advancements in regularization using convex penalties. Convergence rates are analyzed in terms of the sample size in a probabilistic sense, yielding minimax rates in both expectation and probability. To achieve these results, the structure of reproducing kernel Hilbert spaces is leveraged to establish minimax rates in the statistical learning setting. We detail the assumptions underpinning these key elements of our proofs. Finally, we demonstrate the application of these concepts to nonlinear inverse problems in pharmacokinetic/pharmacodynamic (PK/PD) models, where the task is to predict changes in drug concentrations in patients.

Bayesian Posterior Perturbation Analysis with Integral Probability Metrics

In recent years, Bayesian inference in large-scale inverse problems found in science, engineering and machine learning has gained significant attention. This paper examines the robustness of the Bayesian approach by analyzing the stability of posterior measures in relation to perturbations in the likelihood potential and the prior measure. We present new stability results using a family of integral probability metrics (divergences) akin to dual problems that arise in optimal transport. Our results stand out from previous works in three directions: (1) We construct new families of integral probability metrics that are adapted to the problem at hand; (2) These new metrics allow us to study both likelihood and prior perturbations in a convenient way; and (3) our analysis accommodates likelihood potentials that are only locally Lipschitz, making them applicable to a wide range of nonlinear inverse problems. Our theoretical findings are further reinforced through specific and novel examples where the approximation rates of posterior measures are obtained for different types of perturbations and provide a path towards the convergence analysis of recently adapted machine learning techniques for Bayesian inverse problems such as data-driven priors and neural network surrogates.

Introduction To Gaussian Process Regression In Bayesian Inverse Problems, With New ResultsOn Experimental Design For Weighted Error Measures

Bayesian posterior distributions arising in modern applications, including inverse problems in partial differential equation models in tomography and subsurface flow, are often computationally intractable due to the large computational cost of evaluating the data likelihood. To alleviate this problem, we consider using Gaussian process regression to build a surrogate model for the likelihood, resulting in an approximate posterior distribution that is amenable to computations in practice. This work serves as an introduction to Gaussian process regression, in particular in the context of building surrogate models for inverse problems, and presents new insights into a suitable choice of training points. We show that the error between the true and approximate posterior distribution can be bounded by the error between the true and approximate likelihood, measured in the $L^2$-norm weighted by the true posterior, and that efficiently bounding the error between the true and approximate likelihood in this norm suggests choosing the training points in the Gaussian process surrogate model based on the true posterior.

Convex regularization in statistical inverse learning problems

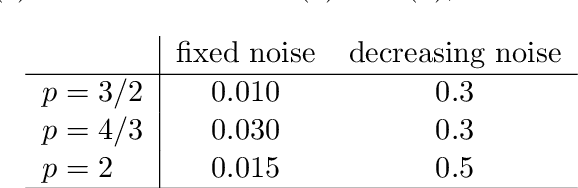
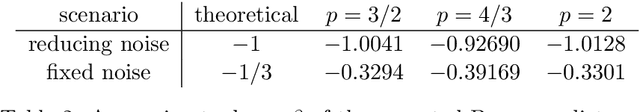
We consider a statistical inverse learning problem, where the task is to estimate a function $f$ based on noisy point evaluations of $Af$, where $A$ is a linear operator. The function $Af$ is evaluated at i.i.d. random design points $u_n$, $n=1,...,N$ generated by an unknown general probability distribution. We consider Tikhonov regularization with general convex and $p$-homogeneous penalty functionals and derive concentration rates of the regularized solution to the ground truth measured in the symmetric Bregman distance induced by the penalty functional. We derive concrete rates for Besov norm penalties and numerically demonstrate the correspondence with the observed rates in the context of X-ray tomography.