The learned range test method for the inverse inclusion problem

We consider the inverse problem consisting of the reconstruction of an inclusion $B$ contained in a bounded domain $\Omega\subset\mathbb{R}^d$ from a single pair of Cauchy data $(u|_{\partial\Omega},\partial_\nu u|_{\partial\Omega})$, where $\Delta u=0$ in $\Omega\setminus\overline B$ and $u=0$ on $\partial B$. We show that the reconstruction algorithm based on the range test, a domain sampling method, can be written as a neural network with a specific architecture. We propose to learn the weights of this network in the framework of supervised learning, and to combine it with a pre-trained classifier, with the purpose of distinguishing the inclusions based on their distance from the boundary. The numerical simulations show that this learned range test method provides accurate and stable reconstructions of polygonal inclusions. Furthermore, the results are superior to those obtained with the standard range test method (without learning) and with an end-to-end fully connected deep neural network, a purely data-driven method.

Learning a Gaussian Mixture for Sparsity Regularization in Inverse Problems

In inverse problems, it is widely recognized that the incorporation of a sparsity prior yields a regularization effect on the solution. This approach is grounded on the a priori assumption that the unknown can be appropriately represented in a basis with a limited number of significant components, while most coefficients are close to zero. This occurrence is frequently observed in real-world scenarios, such as with piecewise smooth signals. In this study, we propose a probabilistic sparsity prior formulated as a mixture of degenerate Gaussians, capable of modeling sparsity with respect to a generic basis. Under this premise, we design a neural network that can be interpreted as the Bayes estimator for linear inverse problems. Additionally, we put forth both a supervised and an unsupervised training strategy to estimate the parameters of this network. To evaluate the effectiveness of our approach, we conduct a numerical comparison with commonly employed sparsity-promoting regularization techniques, namely LASSO, group LASSO, iterative hard thresholding, and sparse coding/dictionary learning. Notably, our reconstructions consistently exhibit lower mean square error values across all $1$D datasets utilized for the comparisons, even in cases where the datasets significantly deviate from a Gaussian mixture model.

Manifold Learning by Mixture Models of VAEs for Inverse Problems

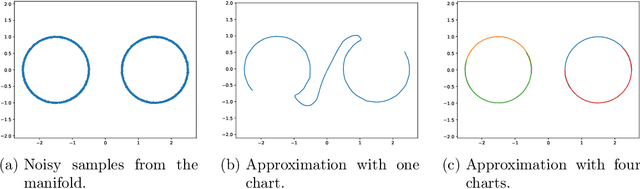
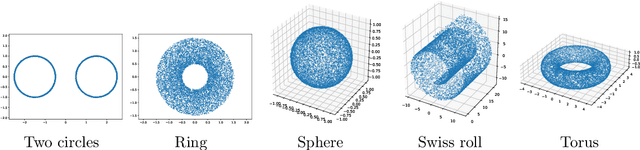
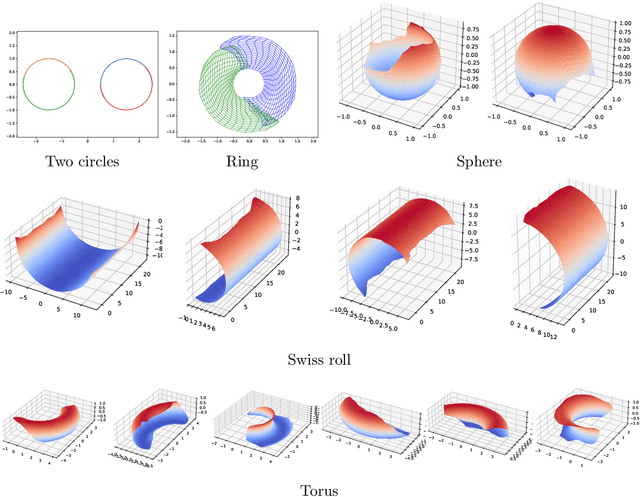
Representing a manifold of very high-dimensional data with generative models has been shown to be computationally efficient in practice. However, this requires that the data manifold admits a global parameterization. In order to represent manifolds of arbitrary topology, we propose to learn a mixture model of variational autoencoders. Here, every encoder-decoder pair represents one chart of a manifold. We propose a loss function for maximum likelihood estimation of the model weights and choose an architecture that provides us the analytical expression of the charts and of their inverses. Once the manifold is learned, we use it for solving inverse problems by minimizing a data fidelity term restricted to the learned manifold. To solve the arising minimization problem we propose a Riemannian gradient descent algorithm on the learned manifold. We demonstrate the performance of our method for low-dimensional toy examples as well as for deblurring and electrical impedance tomography on certain image manifolds.

Localized adversarial artifacts for compressed sensing MRI

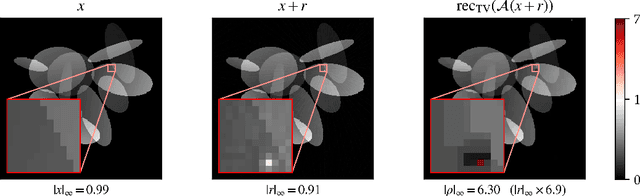
As interest in deep neural networks (DNNs) for image reconstruction tasks grows, their reliability has been called into question (Antun et al., 2020; Gottschling et al., 2020). However, recent work has shown that compared to total variation (TV) minimization, they show similar robustness to adversarial noise in terms of $\ell^2$-reconstruction error (Genzel et al., 2022). We consider a different notion of robustness, using the $\ell^\infty$-norm, and argue that localized reconstruction artifacts are a more relevant defect than the $\ell^2$-error. We create adversarial perturbations to undersampled MRI measurements which induce severe localized artifacts in the TV-regularized reconstruction. The same attack method is not as effective against DNN based reconstruction. Finally, we show that this phenomenon is inherent to reconstruction methods for which exact recovery can be guaranteed, as with compressed sensing reconstructions with $\ell^1$- or TV-minimization.

Continuous Generative Neural Networks

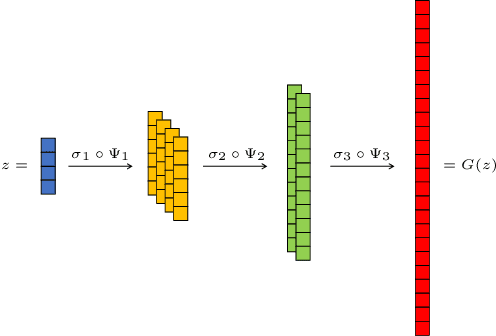
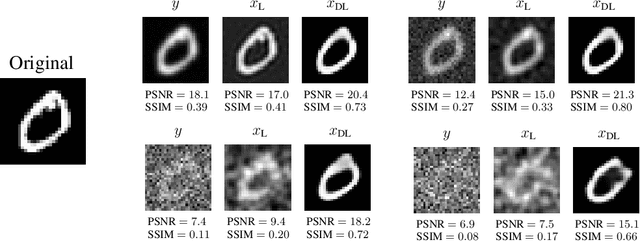
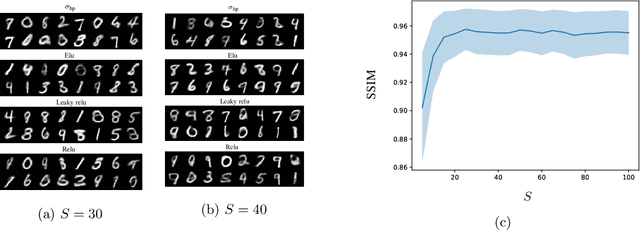
In this work, we present and study Continuous Generative Neural Networks (CGNNs), namely, generative models in the continuous setting. The architecture is inspired by DCGAN, with one fully connected layer, several convolutional layers and nonlinear activation functions. In the continuous $L^2$ setting, the dimensions of the spaces of each layer are replaced by the scales of a multiresolution analysis of a compactly supported wavelet. We present conditions on the convolutional filters and on the nonlinearity that guarantee that a CGNN is injective. This theory finds applications to inverse problems, and allows for deriving Lipschitz stability estimates for (possibly nonlinear) infinite-dimensional inverse problems with unknowns belonging to the manifold generated by a CGNN. Several numerical simulations, including image deblurring, illustrate and validate this approach.

Learning the optimal regularizer for inverse problems

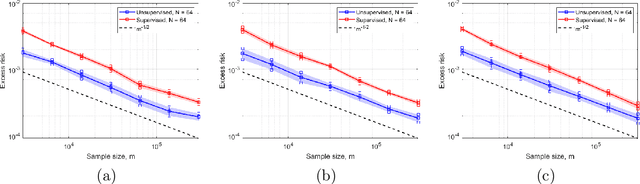
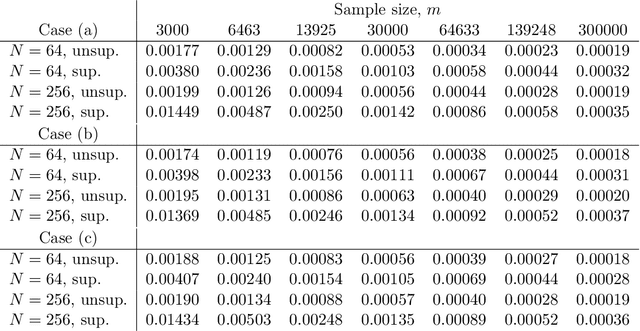
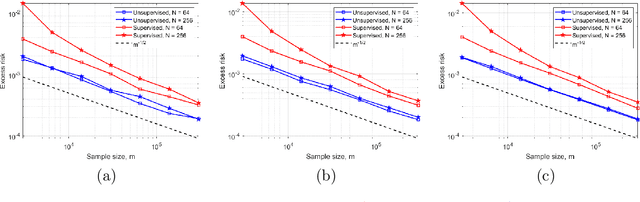
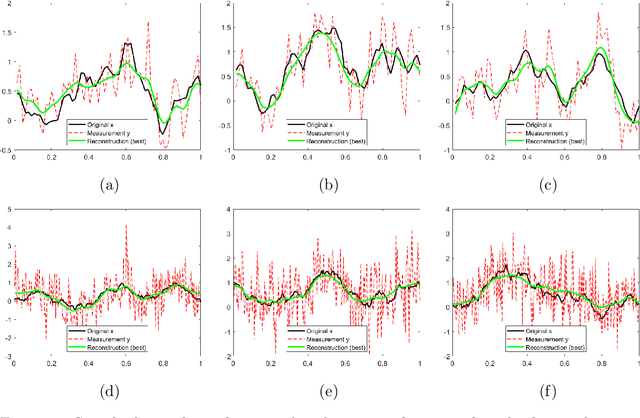
In this work, we consider the linear inverse problem $y=Ax+\epsilon$, where $A\colon X\to Y$ is a known linear operator between the separable Hilbert spaces $X$ and $Y$, $x$ is a random variable in $X$ and $\epsilon$ is a zero-mean random process in $Y$. This setting covers several inverse problems in imaging including denoising, deblurring, and X-ray tomography. Within the classical framework of regularization, we focus on the case where the regularization functional is not given a priori but learned from data. Our first result is a characterization of the optimal generalized Tikhonov regularizer, with respect to the mean squared error. We find that it is completely independent of the forward operator $A$ and depends only on the mean and covariance of $x$. Then, we consider the problem of learning the regularizer from a finite training set in two different frameworks: one supervised, based on samples of both $x$ and $y$, and one unsupervised, based only on samples of $x$. In both cases, we prove generalization bounds, under some weak assumptions on the distribution of $x$ and $\epsilon$, including the case of sub-Gaussian variables. Our bounds hold in infinite-dimensional spaces, thereby showing that finer and finer discretizations do not make this learning problem harder. The results are validated through numerical simulations.

ADef: an Iterative Algorithm to Construct Adversarial Deformations

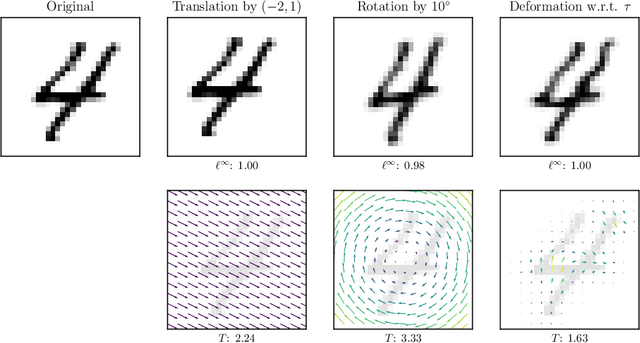
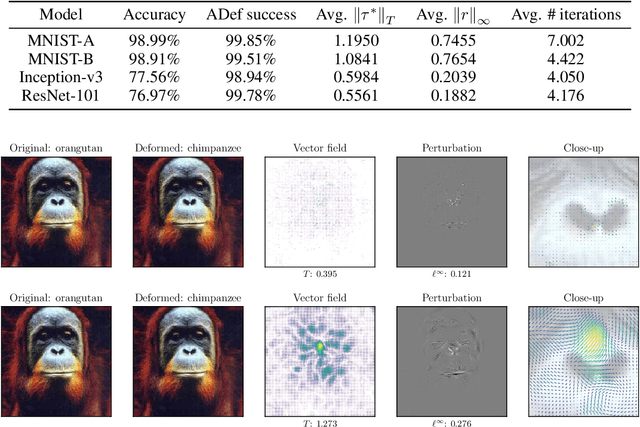
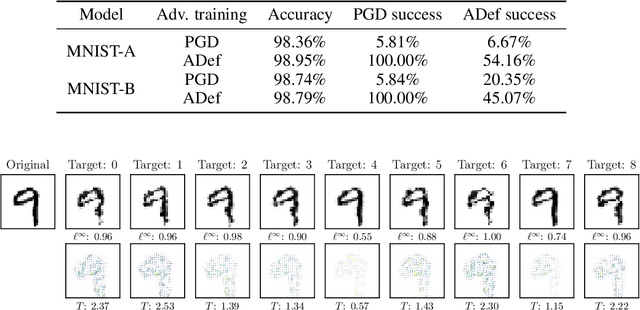
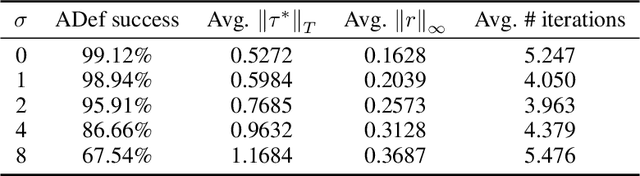
While deep neural networks have proven to be a powerful tool for many recognition and classification tasks, their stability properties are still not well understood. In the past, image classifiers have been shown to be vulnerable to so-called adversarial attacks, which are created by additively perturbing the correctly classified image. In this paper, we propose the ADef algorithm to construct a different kind of adversarial attack created by iteratively applying small deformations to the image, found through a gradient descent step. We demonstrate our results on MNIST with a convolutional neural network and on ImageNet with Inception-v3 and ResNet-101.