Scalable Signature Kernel Computations for Long Time Series via Local Neumann Series Expansions

The signature kernel is a recent state-of-the-art tool for analyzing high-dimensional sequential data, valued for its theoretical guarantees and strong empirical performance. In this paper, we present a novel method for efficiently computing the signature kernel of long, high-dimensional time series via dynamically truncated recursive local power series expansions. Building on the characterization of the signature kernel as the solution of a Goursat PDE, our approach employs tilewise Neumann-series expansions to derive rapidly converging power series approximations of the signature kernel that are locally defined on subdomains and propagated iteratively across the entire domain of the Goursat solution by exploiting the geometry of the time series. Algorithmically, this involves solving a system of interdependent local Goursat PDEs by recursively propagating boundary conditions along a directed graph via topological ordering, with dynamic truncation adaptively terminating each local power series expansion when coefficients fall below machine precision, striking an effective balance between computational cost and accuracy. This method achieves substantial performance improvements over state-of-the-art approaches for computing the signature kernel, providing (a) adjustable and superior accuracy, even for time series with very high roughness; (b) drastically reduced memory requirements; and (c) scalability to efficiently handle very long time series (e.g., with up to half a million points or more) on a single GPU. These advantages make our method particularly well-suited for rough-path-assisted machine learning, financial modeling, and signal processing applications that involve very long and highly volatile data.

Are Neural Operators Really Neural Operators? Frame Theory Meets Operator Learning

Recently, there has been significant interest in operator learning, i.e. learning mappings between infinite-dimensional function spaces. This has been particularly relevant in the context of learning partial differential equations from data. However, it has been observed that proposed models may not behave as operators when implemented on a computer, questioning the very essence of what operator learning should be. We contend that in addition to defining the operator at the continuous level, some form of continuous-discrete equivalence is necessary for an architecture to genuinely learn the underlying operator, rather than just discretizations of it. To this end, we propose to employ frames, a concept in applied harmonic analysis and signal processing that gives rise to exact and stable discrete representations of continuous signals. Extending these concepts to operators, we introduce a unifying mathematical framework of Representation equivalent Neural Operator (ReNO) to ensure operations at the continuous and discrete level are equivalent. Lack of this equivalence is quantified in terms of aliasing errors. We analyze various existing operator learning architectures to determine whether they fall within this framework, and highlight implications when they fail to do so.

Localized adversarial artifacts for compressed sensing MRI

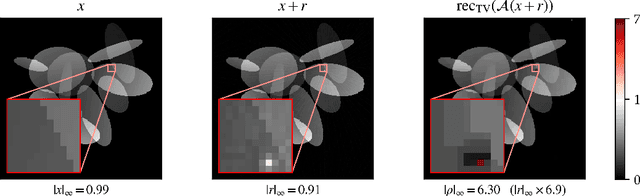
As interest in deep neural networks (DNNs) for image reconstruction tasks grows, their reliability has been called into question (Antun et al., 2020; Gottschling et al., 2020). However, recent work has shown that compared to total variation (TV) minimization, they show similar robustness to adversarial noise in terms of $\ell^2$-reconstruction error (Genzel et al., 2022). We consider a different notion of robustness, using the $\ell^\infty$-norm, and argue that localized reconstruction artifacts are a more relevant defect than the $\ell^2$-error. We create adversarial perturbations to undersampled MRI measurements which induce severe localized artifacts in the TV-regularized reconstruction. The same attack method is not as effective against DNN based reconstruction. Finally, we show that this phenomenon is inherent to reconstruction methods for which exact recovery can be guaranteed, as with compressed sensing reconstructions with $\ell^1$- or TV-minimization.

ADef: an Iterative Algorithm to Construct Adversarial Deformations

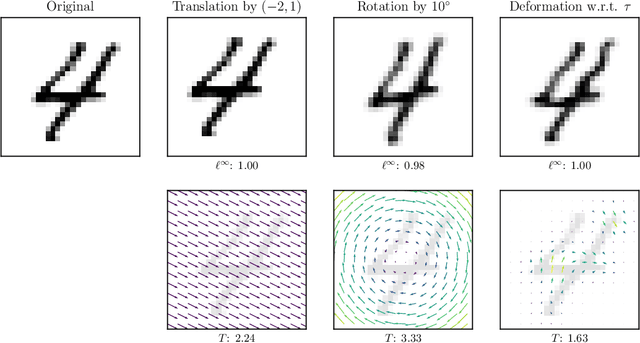
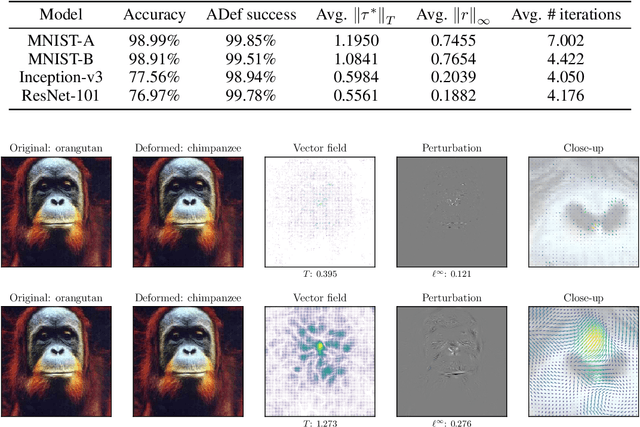
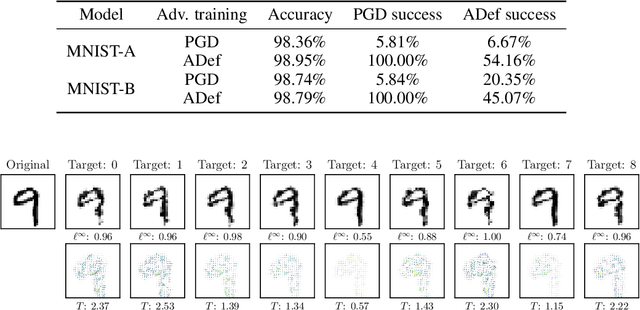
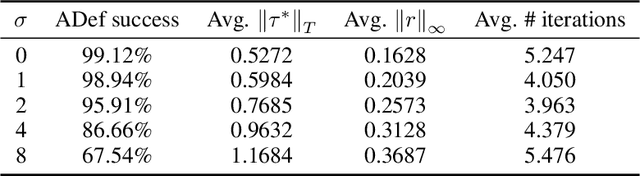
While deep neural networks have proven to be a powerful tool for many recognition and classification tasks, their stability properties are still not well understood. In the past, image classifiers have been shown to be vulnerable to so-called adversarial attacks, which are created by additively perturbing the correctly classified image. In this paper, we propose the ADef algorithm to construct a different kind of adversarial attack created by iteratively applying small deformations to the image, found through a gradient descent step. We demonstrate our results on MNIST with a convolutional neural network and on ImageNet with Inception-v3 and ResNet-101.