EPT-1.5 Technical Report

We announce the release of EPT-1.5, the latest iteration in our Earth Physics Transformer (EPT) family of foundation AI earth system models. EPT-1.5 demonstrates substantial improvements over its predecessor, EPT-1. Built specifically for the European energy industry, EPT-1.5 shows remarkable performance in predicting energy-relevant variables, particularly 10m & 100m wind speed and solar radiation. Especially in wind prediction, it outperforms existing AI weather models like GraphCast, FuXi, and Pangu-Weather, as well as the leading numerical weather model, IFS HRES by the European Centre for Medium-Range Weather Forecasts (ECMWF), setting a new state of the art.

Generative AI for fast and accurate Statistical Computation of Fluids

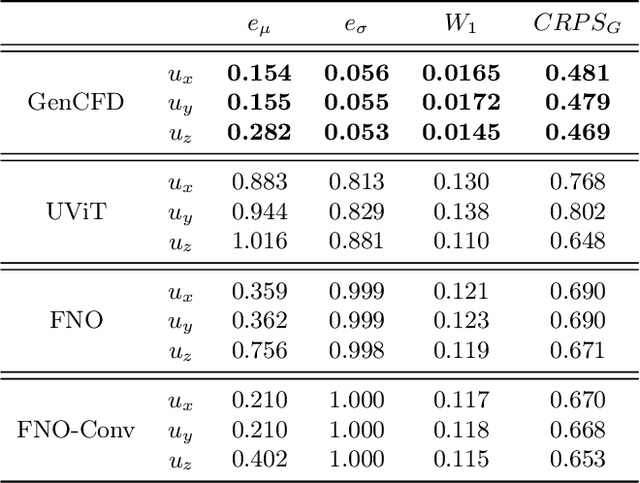
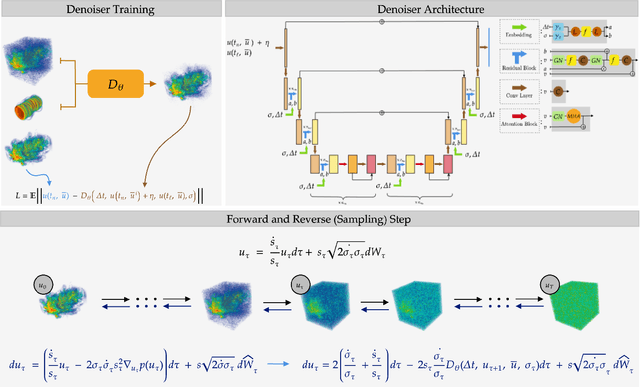
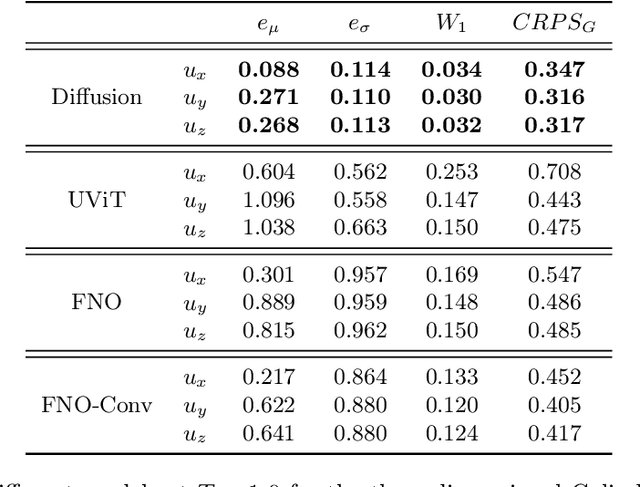
We present a generative AI algorithm for addressing the challenging task of fast, accurate and robust statistical computation of three-dimensional turbulent fluid flows. Our algorithm, termed as GenCFD, is based on a conditional score-based diffusion model. Through extensive numerical experimentation with both incompressible and compressible fluid flows, we demonstrate that GenCFD provides very accurate approximation of statistical quantities of interest such as mean, variance, point pdfs, higher-order moments, while also generating high quality realistic samples of turbulent fluid flows and ensuring excellent spectral resolution. In contrast, ensembles of operator learning baselines which are trained to minimize mean (absolute) square errors regress to the mean flow. We present rigorous theoretical results uncovering the surprising mechanisms through which diffusion models accurately generate fluid flows. These mechanisms are illustrated with solvable toy models that exhibit the relevant features of turbulent fluid flows while being amenable to explicit analytical formulas.

Poseidon: Efficient Foundation Models for PDEs

We introduce Poseidon, a foundation model for learning the solution operators of PDEs. It is based on a multiscale operator transformer, with time-conditioned layer norms that enable continuous-in-time evaluations. A novel training strategy leveraging the semi-group property of time-dependent PDEs to allow for significant scaling-up of the training data is also proposed. Poseidon is pretrained on a diverse, large scale dataset for the governing equations of fluid dynamics. It is then evaluated on a suite of 15 challenging downstream tasks that include a wide variety of PDE types and operators. We show that Poseidon exhibits excellent performance across the board by outperforming baselines significantly, both in terms of sample efficiency and accuracy. Poseidon also generalizes very well to new physics that is not seen during pretraining. Moreover, Poseidon scales with respect to model and data size, both for pretraining and for downstream tasks. Taken together, our results showcase the surprising ability of Poseidon to learn effective representations from a very small set of PDEs during pretraining in order to generalize well to unseen and unrelated PDEs downstream, demonstrating its potential as an effective, general purpose PDE foundation model. Finally, the Poseidon model as well as underlying pretraining and downstream datasets are open sourced, with code being available at https://github.com/camlab-ethz/poseidon and pretrained models and datasets at https://huggingface.co/camlab-ethz.

Are Neural Operators Really Neural Operators? Frame Theory Meets Operator Learning

Recently, there has been significant interest in operator learning, i.e. learning mappings between infinite-dimensional function spaces. This has been particularly relevant in the context of learning partial differential equations from data. However, it has been observed that proposed models may not behave as operators when implemented on a computer, questioning the very essence of what operator learning should be. We contend that in addition to defining the operator at the continuous level, some form of continuous-discrete equivalence is necessary for an architecture to genuinely learn the underlying operator, rather than just discretizations of it. To this end, we propose to employ frames, a concept in applied harmonic analysis and signal processing that gives rise to exact and stable discrete representations of continuous signals. Extending these concepts to operators, we introduce a unifying mathematical framework of Representation equivalent Neural Operator (ReNO) to ensure operations at the continuous and discrete level are equivalent. Lack of this equivalence is quantified in terms of aliasing errors. We analyze various existing operator learning architectures to determine whether they fall within this framework, and highlight implications when they fail to do so.

Convolutional Neural Operators

Although very successfully used in machine learning, convolution based neural network architectures -- believed to be inconsistent in function space -- have been largely ignored in the context of learning solution operators of PDEs. Here, we adapt convolutional neural networks to demonstrate that they are indeed able to process functions as inputs and outputs. The resulting architecture, termed as convolutional neural operators (CNOs), is shown to significantly outperform competing models on benchmark experiments, paving the way for the design of an alternative robust and accurate framework for learning operators.

Neural Inverse Operators for Solving PDE Inverse Problems

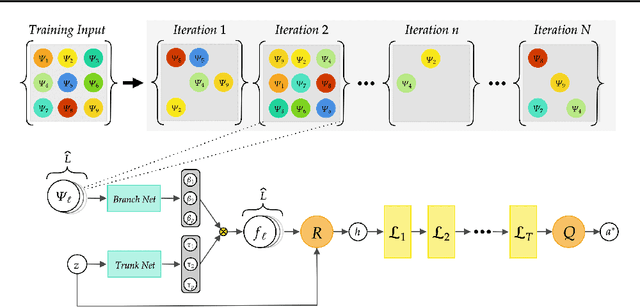
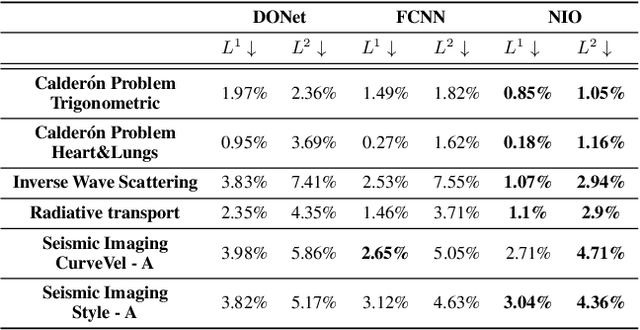
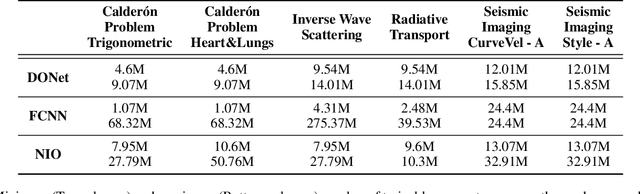
A large class of inverse problems for PDEs are only well-defined as mappings from operators to functions. Existing operator learning frameworks map functions to functions and need to be modified to learn inverse maps from data. We propose a novel architecture termed Neural Inverse Operators (NIOs) to solve these PDE inverse problems. Motivated by the underlying mathematical structure, NIO is based on a suitable composition of DeepONets and FNOs to approximate mappings from operators to functions. A variety of experiments are presented to demonstrate that NIOs significantly outperform baselines and solve PDE inverse problems robustly, accurately and are several orders of magnitude faster than existing direct and PDE-constrained optimization methods.

Nonlinear Reconstruction for Operator Learning of PDEs with Discontinuities

A large class of hyperbolic and advection-dominated PDEs can have solutions with discontinuities. This paper investigates, both theoretically and empirically, the operator learning of PDEs with discontinuous solutions. We rigorously prove, in terms of lower approximation bounds, that methods which entail a linear reconstruction step (e.g. DeepONet or PCA-Net) fail to efficiently approximate the solution operator of such PDEs. In contrast, we show that certain methods employing a non-linear reconstruction mechanism can overcome these fundamental lower bounds and approximate the underlying operator efficiently. The latter class includes Fourier Neural Operators and a novel extension of DeepONet termed shift-DeepONet. Our theoretical findings are confirmed by empirical results for advection equation, inviscid Burgers' equation and compressible Euler equations of aerodynamics.

wPINNs: Weak Physics informed neural networks for approximating entropy solutions of hyperbolic conservation laws

Physics informed neural networks (PINNs) require regularity of solutions of the underlying PDE to guarantee accurate approximation. Consequently, they may fail at approximating discontinuous solutions of PDEs such as nonlinear hyperbolic equations. To ameliorate this, we propose a novel variant of PINNs, termed as weak PINNs (wPINNs) for accurate approximation of entropy solutions of scalar conservation laws. wPINNs are based on approximating the solution of a min-max optimization problem for a residual, defined in terms of Kruzkhov entropies, to determine parameters for the neural networks approximating the entropy solution as well as test functions. We prove rigorous bounds on the error incurred by wPINNs and illustrate their performance through numerical experiments to demonstrate that wPINNs can approximate entropy solutions accurately.

Physics Informed Neural Networks for Simulating Radiative Transfer

We propose a novel machine learning algorithm for simulating radiative transfer. Our algorithm is based on physics informed neural networks (PINNs), which are trained by minimizing the residual of the underlying radiative tranfer equations. We present extensive experiments and theoretical error estimates to demonstrate that PINNs provide a very easy to implement, fast, robust and accurate method for simulating radiative transfer. We also present a PINN based algorithm for simulating inverse problems for radiative transfer efficiently.

Estimates on the generalization error of Physics Informed Neural Networks (PINNs) for approximating PDEs II: A class of inverse problems

Physics informed neural networks (PINNs) have recently been very successfully applied for efficiently approximating inverse problems for PDEs. We focus on a particular class of inverse problems, the so-called data assimilation or unique continuation problems, and prove rigorous estimates on the generalization error of PINNs approximating them. An abstract framework is presented and conditional stability estimates for the underlying inverse problem are employed to derive the estimate on the PINN generalization error, providing rigorous justification for the use of PINNs in this context. The abstract framework is illustrated with examples of four prototypical linear PDEs. Numerical experiments, validating the proposed theory, are also presented.