Imposing Boundary Conditions on Neural Operators via Learned Function Extensions

Neural operators have emerged as powerful surrogates for the solution of partial differential equations (PDEs), yet their ability to handle general, highly variable boundary conditions (BCs) remains limited. Existing approaches often fail when the solution operator exhibits strong sensitivity to boundary forcings. We propose a general framework for conditioning neural operators on complex non-homogeneous BCs through function extensions. Our key idea is to map boundary data to latent pseudo-extensions defined over the entire spatial domain, enabling any standard operator learning architecture to consume boundary information. The resulting operator, coupled with an arbitrary domain-to-domain neural operator, can learn rich dependencies on complex BCs and input domain functions at the same time. To benchmark this setting, we construct 18 challenging datasets spanning Poisson, linear elasticity, and hyperelasticity problems, with highly variable, mixed-type, component-wise, and multi-segment BCs on diverse geometries. Our approach achieves state-of-the-art accuracy, outperforming baselines by large margins, while requiring no hyperparameter tuning across datasets. Overall, our results demonstrate that learning boundary-to-domain extensions is an effective and practical strategy for imposing complex BCs in existing neural operator frameworks, enabling accurate and robust scientific machine learning models for a broader range of PDE-governed problems.

Learning, Solving and Optimizing PDEs with TensorGalerkin: an efficient high-performance Galerkin assembly algorithm

We present a unified algorithmic framework for the numerical solution, constrained optimization, and physics-informed learning of PDEs with a variational structure. Our framework is based on a Galerkin discretization of the underlying variational forms, and its high efficiency stems from a novel highly-optimized and GPU-compliant TensorGalerkin framework for linear system assembly (stiffness matrices and load vectors). TensorGalerkin operates by tensorizing element-wise operations within a Python-level Map stage and then performs global reduction with a sparse matrix multiplication that performs message passing on the mesh-induced sparsity graph. It can be seamlessly employed downstream as i) a highly-efficient numerical PDEs solver, ii) an end-to-end differentiable framework for PDE-constrained optimization, and iii) a physics-informed operator learning algorithm for PDEs. With multiple benchmarks, including 2D and 3D elliptic, parabolic, and hyperbolic PDEs on unstructured meshes, we demonstrate that the proposed framework provides significant computational efficiency and accuracy gains over a variety of baselines in all the targeted downstream applications.

Phaedra: Learning High-Fidelity Discrete Tokenization for the Physical Science

Tokens are discrete representations that allow modern deep learning to scale by transforming high-dimensional data into sequences that can be efficiently learned, generated, and generalized to new tasks. These have become foundational for image and video generation and, more recently, physical simulation. As existing tokenizers are designed for the explicit requirements of realistic visual perception of images, it is necessary to ask whether these approaches are optimal for scientific images, which exhibit a large dynamic range and require token embeddings to retain physical and spectral properties. In this work, we investigate the accuracy of a suite of image tokenizers across a range of metrics designed to measure the fidelity of PDE properties in both physical and spectral space. Based on the observation that these struggle to capture both fine details and precise magnitudes, we propose Phaedra, inspired by classical shape-gain quantization and proper orthogonal decomposition. We demonstrate that Phaedra consistently improves reconstruction across a range of PDE datasets. Additionally, our results show strong out-of-distribution generalization capabilities to three tasks of increasing complexity, namely known PDEs with different conditions, unknown PDEs, and real-world Earth observation and weather data.

Gauss-Newton Natural Gradient Descent for Shape Learning

We explore the use of the Gauss-Newton method for optimization in shape learning, including implicit neural surfaces and geometry-informed neural networks. The method addresses key challenges in shape learning, such as the ill-conditioning of the underlying differential constraints and the mismatch between the optimization problem in parameter space and the function space where the problem is naturally posed. This leads to significantly faster and more stable convergence than standard first-order methods, while also requiring far fewer iterations. Experiments across benchmark shape optimization tasks demonstrate that the Gauss-Newton method consistently improves both training speed and final solution accuracy.

Out-of-Distribution Detection in Molecular Complexes via Diffusion Models for Irregular Graphs

Predictive machine learning models generally excel on in-distribution data, but their performance degrades on out-of-distribution (OOD) inputs. Reliable deployment therefore requires robust OOD detection, yet this is particularly challenging for irregular 3D graphs that combine continuous geometry with categorical identities and are unordered by construction. Here, we present a probabilistic OOD detection framework for complex 3D graph data built on a diffusion model that learns a density of the training distribution in a fully unsupervised manner. A key ingredient we introduce is a unified continuous diffusion over both 3D coordinates and discrete features: categorical identities are embedded in a continuous space and trained with cross-entropy, while the corresponding diffusion score is obtained analytically via posterior-mean interpolation from predicted class probabilities. This yields a single self-consistent probability-flow ODE (PF-ODE) that produces per-sample log-likelihoods, providing a principled typicality score for distribution shift. We validate the approach on protein-ligand complexes and construct strict OOD datasets by withholding entire protein families from training. PF-ODE likelihoods identify held-out families as OOD and correlate strongly with prediction errors of an independent binding-affinity model (GEMS), enabling a priori reliability estimates on new complexes. Beyond scalar likelihoods, we show that multi-scale PF-ODE trajectory statistics - including path tortuosity, flow stiffness, and vector-field instability - provide complementary OOD information. Modeling the joint distribution of these trajectory features yields a practical, high-sensitivity detector that improves separation over likelihood-only baselines, offering a label-free OOD quantification workflow for geometric deep learning.

HyPINO: Multi-Physics Neural Operators via HyperPINNs and the Method of Manufactured Solutions

We present HyPINO, a multi-physics neural operator designed for zero-shot generalization across a broad class of parametric PDEs without requiring task-specific fine-tuning. Our approach combines a Swin Transformer-based hypernetwork with mixed supervision: (i) labeled data from analytical solutions generated via the Method of Manufactured Solutions (MMS), and (ii) unlabeled samples optimized using physics-informed objectives. The model maps PDE parametrizations to target Physics-Informed Neural Networks (PINNs) and can handle linear elliptic, hyperbolic, and parabolic equations in two dimensions with varying source terms, geometries, and mixed Dirichlet/Neumann boundary conditions, including interior boundaries. HyPINO achieves strong zero-shot accuracy on seven benchmark problems from PINN literature, outperforming U-Nets, Poseidon, and Physics-Informed Neural Operators (PINO). Further, we introduce an iterative refinement procedure that compares the physics of the generated PINN to the requested PDE and uses the discrepancy to generate a "delta" PINN. Summing their contributions and repeating this process forms an ensemble whose combined solution progressively reduces the error on six benchmarks and achieves over 100x gain in average $L_2$ loss in the best case, while retaining forward-only inference. Additionally, we evaluate the fine-tuning behavior of PINNs initialized by HyPINO and show that they converge faster and to lower final error than both randomly initialized and Reptile-meta-learned PINNs on five benchmarks, performing on par on the remaining two. Our results highlight the potential of this scalable approach as a foundation for extending neural operators toward solving increasingly complex, nonlinear, and high-dimensional PDE problems with significantly improved accuracy and reduced computational cost.

Finetuning a Weather Foundation Model with Lightweight Decoders for Unseen Physical Processes

Recent advances in AI weather forecasting have led to the emergence of so-called "foundation models", typically defined by expensive pretraining and minimal fine-tuning for downstream tasks. However, in the natural sciences, a desirable foundation model should also encode meaningful statistical relationships between the underlying physical variables. This study evaluates the performance of the state-of-the-art Aurora foundation model in predicting hydrological variables, which were not considered during pretraining. We introduce a lightweight approach using shallow decoders trained on the latent representations of the pretrained model to predict these new variables. As a baseline, we compare this to fine-tuning the full model, which allows further optimization of the latent space while incorporating new variables into both inputs and outputs. The decoder-based approach requires 50% less training time and 35% less memory, while achieving strong accuracy across various hydrological variables and preserving desirable properties of the foundation model, such as autoregressive stability. Notably, decoder accuracy depends on the physical correlation between the new variables and those used during pretraining, indicating that Aurora's latent space captures meaningful physical relationships. In this sense, we argue that an important quality metric for foundation models in Earth sciences is their ability to be extended to new variables without a full fine-tuning. This provides a new perspective for making foundation models more accessible to communities with limited computational resources, while supporting broader adoption in Earth sciences.

Geometry Aware Operator Transformer as an Efficient and Accurate Neural Surrogate for PDEs on Arbitrary Domains

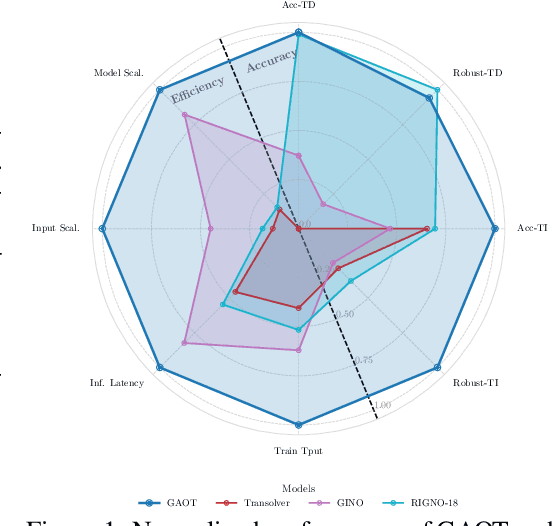
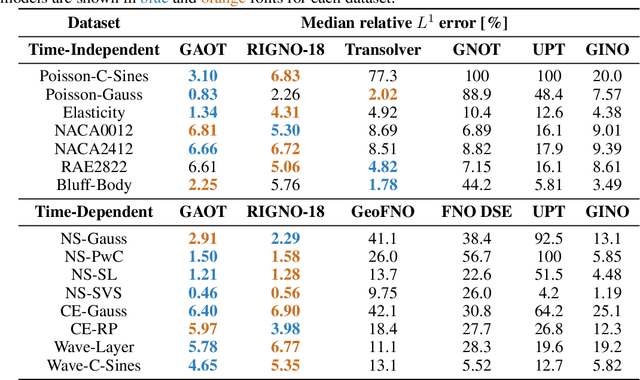
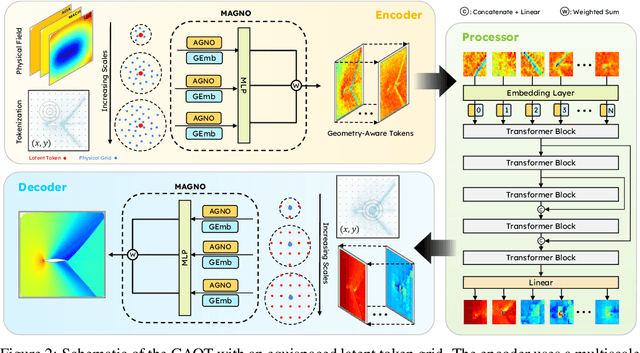
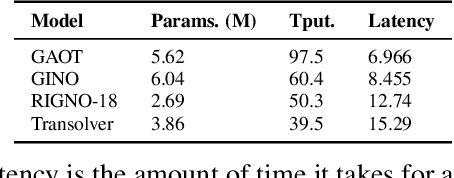
The very challenging task of learning solution operators of PDEs on arbitrary domains accurately and efficiently is of vital importance to engineering and industrial simulations. Despite the existence of many operator learning algorithms to approximate such PDEs, we find that accurate models are not necessarily computationally efficient and vice versa. We address this issue by proposing a geometry aware operator transformer (GAOT) for learning PDEs on arbitrary domains. GAOT combines novel multiscale attentional graph neural operator encoders and decoders, together with geometry embeddings and (vision) transformer processors to accurately map information about the domain and the inputs into a robust approximation of the PDE solution. Multiple innovations in the implementation of GAOT also ensure computational efficiency and scalability. We demonstrate this significant gain in both accuracy and efficiency of GAOT over several baselines on a large number of learning tasks from a diverse set of PDEs, including achieving state of the art performance on a large scale three-dimensional industrial CFD dataset.

Data-Driven, ML-assisted Approaches to Problem Well-Posedness

Classically, to solve differential equation problems, it is necessary to specify sufficient initial and/or boundary conditions so as to allow the existence of a unique solution. Well-posedness of differential equation problems thus involves studying the existence and uniqueness of solutions, and their dependence to such pre-specified conditions. However, in part due to mathematical necessity, these conditions are usually specified "to arbitrary precision" only on (appropriate portions of) the boundary of the space-time domain. This does not mirror how data acquisition is performed in realistic situations, where one may observe entire "patches" of solution data at arbitrary space-time locations; alternatively one might have access to more than one solutions stemming from the same differential operator. In our short work, we demonstrate how standard tools from machine and manifold learning can be used to infer, in a data driven manner, certain well-posedness features of differential equation problems, for initial/boundary condition combinations under which rigorous existence/uniqueness theorems are not known. Our study naturally combines a data assimilation perspective with an operator-learning one.

Neuro-Symbolic AI for Analytical Solutions of Differential Equations

Analytical solutions of differential equations offer exact insights into fundamental behaviors of physical processes. Their application, however, is limited as finding these solutions is difficult. To overcome this limitation, we combine two key insights. First, constructing an analytical solution requires a composition of foundational solution components. Second, iterative solvers define parameterized function spaces with constraint-based updates. Our approach merges compositional differential equation solution techniques with iterative refinement by using formal grammars, building a rich space of candidate solutions that are embedded into a low-dimensional (continuous) latent manifold for probabilistic exploration. This integration unifies numerical and symbolic differential equation solvers via a neuro-symbolic AI framework to find analytical solutions of a wide variety of differential equations. By systematically constructing candidate expressions and applying constraint-based refinement, we overcome longstanding barriers to extract such closed-form solutions. We illustrate advantages over commercial solvers, symbolic methods, and approximate neural networks on a diverse set of problems, demonstrating both generality and accuracy.