Phaedra: Learning High-Fidelity Discrete Tokenization for the Physical Science

Tokens are discrete representations that allow modern deep learning to scale by transforming high-dimensional data into sequences that can be efficiently learned, generated, and generalized to new tasks. These have become foundational for image and video generation and, more recently, physical simulation. As existing tokenizers are designed for the explicit requirements of realistic visual perception of images, it is necessary to ask whether these approaches are optimal for scientific images, which exhibit a large dynamic range and require token embeddings to retain physical and spectral properties. In this work, we investigate the accuracy of a suite of image tokenizers across a range of metrics designed to measure the fidelity of PDE properties in both physical and spectral space. Based on the observation that these struggle to capture both fine details and precise magnitudes, we propose Phaedra, inspired by classical shape-gain quantization and proper orthogonal decomposition. We demonstrate that Phaedra consistently improves reconstruction across a range of PDE datasets. Additionally, our results show strong out-of-distribution generalization capabilities to three tasks of increasing complexity, namely known PDEs with different conditions, unknown PDEs, and real-world Earth observation and weather data.

Geometry Aware Operator Transformer as an Efficient and Accurate Neural Surrogate for PDEs on Arbitrary Domains

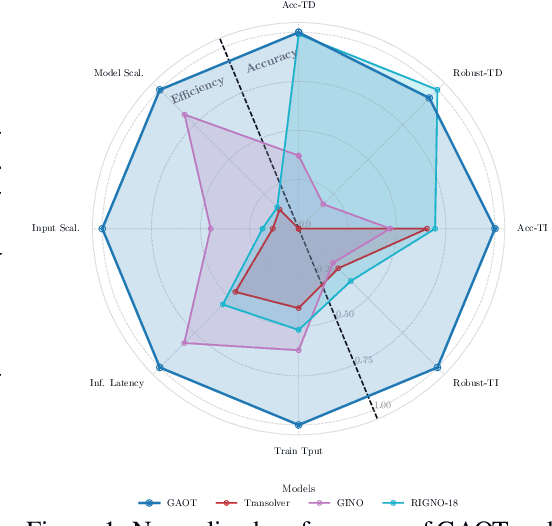
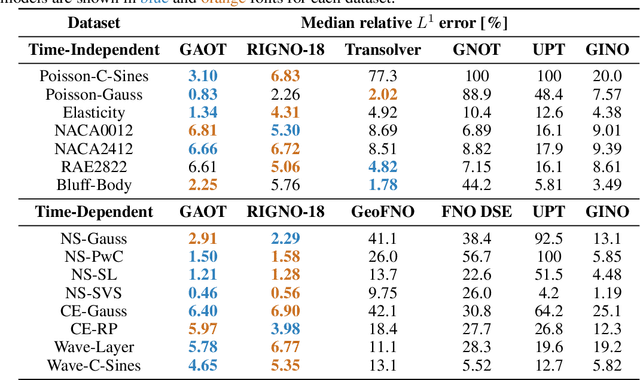
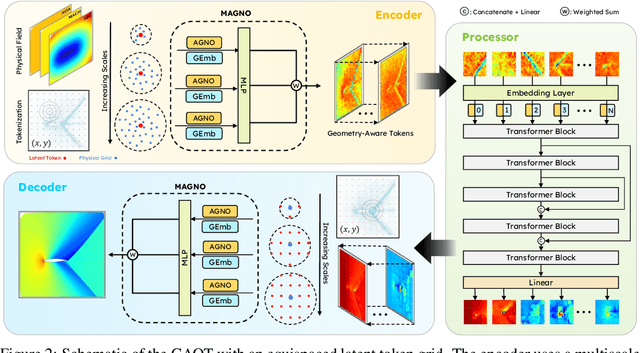
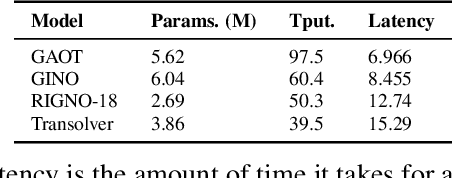
The very challenging task of learning solution operators of PDEs on arbitrary domains accurately and efficiently is of vital importance to engineering and industrial simulations. Despite the existence of many operator learning algorithms to approximate such PDEs, we find that accurate models are not necessarily computationally efficient and vice versa. We address this issue by proposing a geometry aware operator transformer (GAOT) for learning PDEs on arbitrary domains. GAOT combines novel multiscale attentional graph neural operator encoders and decoders, together with geometry embeddings and (vision) transformer processors to accurately map information about the domain and the inputs into a robust approximation of the PDE solution. Multiple innovations in the implementation of GAOT also ensure computational efficiency and scalability. We demonstrate this significant gain in both accuracy and efficiency of GAOT over several baselines on a large number of learning tasks from a diverse set of PDEs, including achieving state of the art performance on a large scale three-dimensional industrial CFD dataset.

A Low-complexity Structured Neural Network to Realize States of Dynamical Systems

Data-driven learning is rapidly evolving and places a new perspective on realizing state-space dynamical systems. However, dynamical systems derived from nonlinear ordinary differential equations (ODEs) suffer from limitations in computational efficiency. Thus, this paper stems from data-driven learning to advance states of dynamical systems utilizing a structured neural network (StNN). The proposed learning technique also seeks to identify an optimal, low-complexity operator to solve dynamical systems, the so-called Hankel operator, derived from time-delay measurements. Thus, we utilize the StNN based on the Hankel operator to solve dynamical systems as an alternative to existing data-driven techniques. We show that the proposed StNN reduces the number of parameters and computational complexity compared with the conventional neural networks and also with the classical data-driven techniques, such as Sparse Identification of Nonlinear Dynamics (SINDy) and Hankel Alternative view of Koopman (HAVOK), which is commonly known as delay-Dynamic Mode Decomposition(DMD) or Hankel-DMD. More specifically, we present numerical simulations to solve dynamical systems utilizing the StNN based on the Hankel operator beginning from the fundamental Lotka-Volterra model, where we compare the StNN with the LEarning Across Dynamical Systems (LEADS), and extend our analysis to highly nonlinear and chaotic Lorenz systems, comparing the StNN with conventional neural networks, SINDy, and HAVOK. Hence, we show that the proposed StNN paves the way for realizing state-space dynamical systems with a low-complexity learning algorithm, enabling prediction and understanding of future states.

Neuro-Symbolic AI for Analytical Solutions of Differential Equations

Analytical solutions of differential equations offer exact insights into fundamental behaviors of physical processes. Their application, however, is limited as finding these solutions is difficult. To overcome this limitation, we combine two key insights. First, constructing an analytical solution requires a composition of foundational solution components. Second, iterative solvers define parameterized function spaces with constraint-based updates. Our approach merges compositional differential equation solution techniques with iterative refinement by using formal grammars, building a rich space of candidate solutions that are embedded into a low-dimensional (continuous) latent manifold for probabilistic exploration. This integration unifies numerical and symbolic differential equation solvers via a neuro-symbolic AI framework to find analytical solutions of a wide variety of differential equations. By systematically constructing candidate expressions and applying constraint-based refinement, we overcome longstanding barriers to extract such closed-form solutions. We illustrate advantages over commercial solvers, symbolic methods, and approximate neural networks on a diverse set of problems, demonstrating both generality and accuracy.

RIGNO: A Graph-based framework for robust and accurate operator learning for PDEs on arbitrary domains

Learning the solution operators of PDEs on arbitrary domains is challenging due to the diversity of possible domain shapes, in addition to the often intricate underlying physics. We propose an end-to-end graph neural network (GNN) based neural operator to learn PDE solution operators from data on point clouds in arbitrary domains. Our multi-scale model maps data between input/output point clouds by passing it through a downsampled regional mesh. Many novel elements are also incorporated to ensure resolution invariance and temporal continuity. Our model, termed RIGNO, is tested on a challenging suite of benchmarks, composed of various time-dependent and steady PDEs defined on a diverse set of domains. We demonstrate that RIGNO is significantly more accurate than neural operator baselines and robustly generalizes to unseen spatial resolutions and time instances.

Vandermonde Neural Operators

Fourier Neural Operators (FNOs) have emerged as very popular machine learning architectures for learning operators, particularly those arising in PDEs. However, as FNOs rely on the fast Fourier transform for computational efficiency, the architecture can be limited to input data on equispaced Cartesian grids. Here, we generalize FNOs to handle input data on non-equispaced point distributions. Our proposed model, termed as Vandermonde Neural Operator (VNO), utilizes Vandermonde-structured matrices to efficiently compute forward and inverse Fourier transforms, even on arbitrarily distributed points. We present numerical experiments to demonstrate that VNOs can be significantly faster than FNOs, while retaining comparable accuracy, and improve upon accuracy of comparable non-equispaced methods such as the Geo-FNO.