Learning, Solving and Optimizing PDEs with TensorGalerkin: an efficient high-performance Galerkin assembly algorithm

We present a unified algorithmic framework for the numerical solution, constrained optimization, and physics-informed learning of PDEs with a variational structure. Our framework is based on a Galerkin discretization of the underlying variational forms, and its high efficiency stems from a novel highly-optimized and GPU-compliant TensorGalerkin framework for linear system assembly (stiffness matrices and load vectors). TensorGalerkin operates by tensorizing element-wise operations within a Python-level Map stage and then performs global reduction with a sparse matrix multiplication that performs message passing on the mesh-induced sparsity graph. It can be seamlessly employed downstream as i) a highly-efficient numerical PDEs solver, ii) an end-to-end differentiable framework for PDE-constrained optimization, and iii) a physics-informed operator learning algorithm for PDEs. With multiple benchmarks, including 2D and 3D elliptic, parabolic, and hyperbolic PDEs on unstructured meshes, we demonstrate that the proposed framework provides significant computational efficiency and accuracy gains over a variety of baselines in all the targeted downstream applications.

Geometry Aware Operator Transformer as an Efficient and Accurate Neural Surrogate for PDEs on Arbitrary Domains

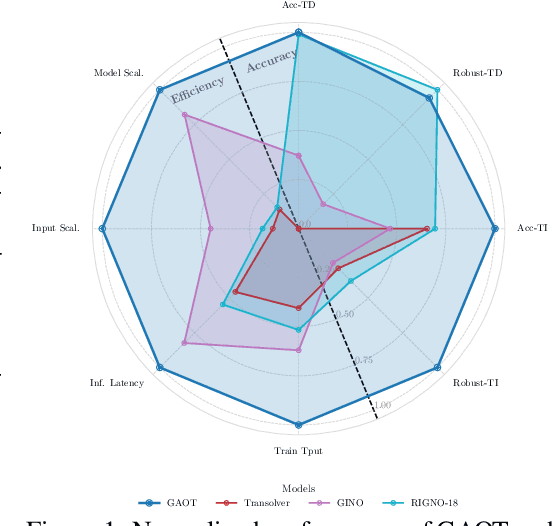
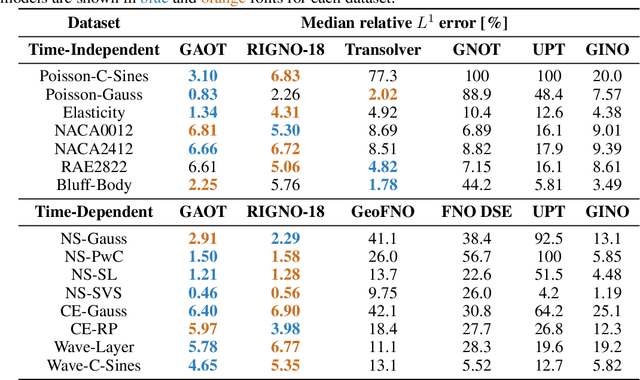
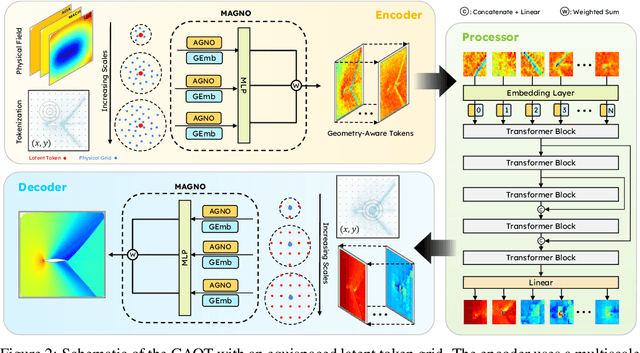
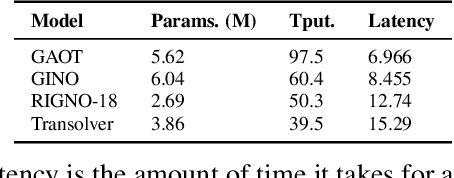
The very challenging task of learning solution operators of PDEs on arbitrary domains accurately and efficiently is of vital importance to engineering and industrial simulations. Despite the existence of many operator learning algorithms to approximate such PDEs, we find that accurate models are not necessarily computationally efficient and vice versa. We address this issue by proposing a geometry aware operator transformer (GAOT) for learning PDEs on arbitrary domains. GAOT combines novel multiscale attentional graph neural operator encoders and decoders, together with geometry embeddings and (vision) transformer processors to accurately map information about the domain and the inputs into a robust approximation of the PDE solution. Multiple innovations in the implementation of GAOT also ensure computational efficiency and scalability. We demonstrate this significant gain in both accuracy and efficiency of GAOT over several baselines on a large number of learning tasks from a diverse set of PDEs, including achieving state of the art performance on a large scale three-dimensional industrial CFD dataset.

RIGNO: A Graph-based framework for robust and accurate operator learning for PDEs on arbitrary domains

Learning the solution operators of PDEs on arbitrary domains is challenging due to the diversity of possible domain shapes, in addition to the often intricate underlying physics. We propose an end-to-end graph neural network (GNN) based neural operator to learn PDE solution operators from data on point clouds in arbitrary domains. Our multi-scale model maps data between input/output point clouds by passing it through a downsampled regional mesh. Many novel elements are also incorporated to ensure resolution invariance and temporal continuity. Our model, termed RIGNO, is tested on a challenging suite of benchmarks, composed of various time-dependent and steady PDEs defined on a diverse set of domains. We demonstrate that RIGNO is significantly more accurate than neural operator baselines and robustly generalizes to unseen spatial resolutions and time instances.