Imposing Boundary Conditions on Neural Operators via Learned Function Extensions

Neural operators have emerged as powerful surrogates for the solution of partial differential equations (PDEs), yet their ability to handle general, highly variable boundary conditions (BCs) remains limited. Existing approaches often fail when the solution operator exhibits strong sensitivity to boundary forcings. We propose a general framework for conditioning neural operators on complex non-homogeneous BCs through function extensions. Our key idea is to map boundary data to latent pseudo-extensions defined over the entire spatial domain, enabling any standard operator learning architecture to consume boundary information. The resulting operator, coupled with an arbitrary domain-to-domain neural operator, can learn rich dependencies on complex BCs and input domain functions at the same time. To benchmark this setting, we construct 18 challenging datasets spanning Poisson, linear elasticity, and hyperelasticity problems, with highly variable, mixed-type, component-wise, and multi-segment BCs on diverse geometries. Our approach achieves state-of-the-art accuracy, outperforming baselines by large margins, while requiring no hyperparameter tuning across datasets. Overall, our results demonstrate that learning boundary-to-domain extensions is an effective and practical strategy for imposing complex BCs in existing neural operator frameworks, enabling accurate and robust scientific machine learning models for a broader range of PDE-governed problems.

Geometry Aware Operator Transformer as an Efficient and Accurate Neural Surrogate for PDEs on Arbitrary Domains

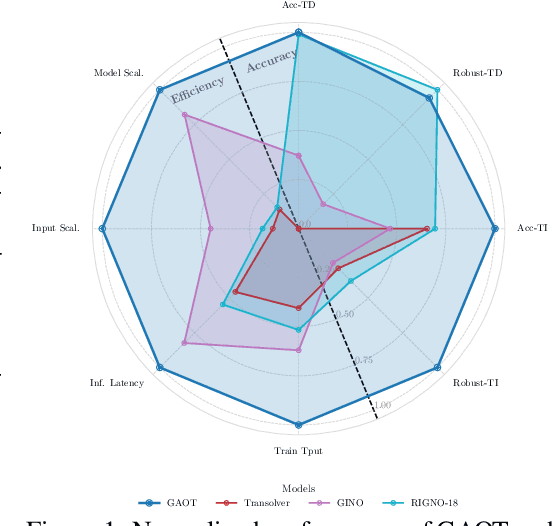
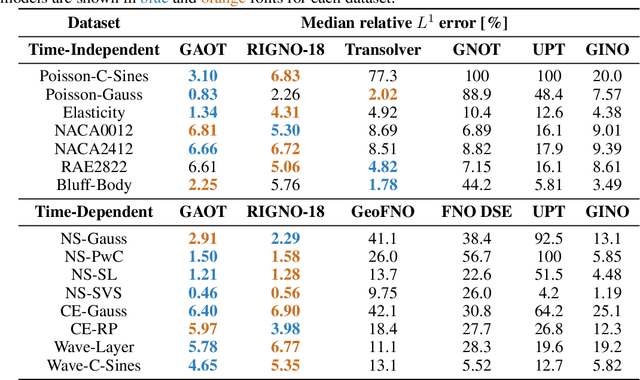
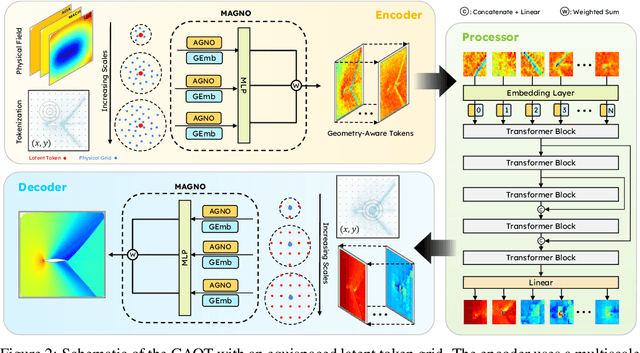
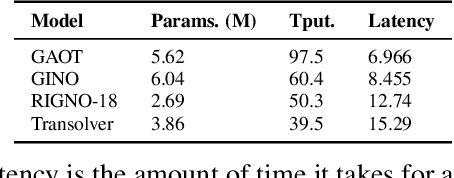
The very challenging task of learning solution operators of PDEs on arbitrary domains accurately and efficiently is of vital importance to engineering and industrial simulations. Despite the existence of many operator learning algorithms to approximate such PDEs, we find that accurate models are not necessarily computationally efficient and vice versa. We address this issue by proposing a geometry aware operator transformer (GAOT) for learning PDEs on arbitrary domains. GAOT combines novel multiscale attentional graph neural operator encoders and decoders, together with geometry embeddings and (vision) transformer processors to accurately map information about the domain and the inputs into a robust approximation of the PDE solution. Multiple innovations in the implementation of GAOT also ensure computational efficiency and scalability. We demonstrate this significant gain in both accuracy and efficiency of GAOT over several baselines on a large number of learning tasks from a diverse set of PDEs, including achieving state of the art performance on a large scale three-dimensional industrial CFD dataset.

RIGNO: A Graph-based framework for robust and accurate operator learning for PDEs on arbitrary domains

Learning the solution operators of PDEs on arbitrary domains is challenging due to the diversity of possible domain shapes, in addition to the often intricate underlying physics. We propose an end-to-end graph neural network (GNN) based neural operator to learn PDE solution operators from data on point clouds in arbitrary domains. Our multi-scale model maps data between input/output point clouds by passing it through a downsampled regional mesh. Many novel elements are also incorporated to ensure resolution invariance and temporal continuity. Our model, termed RIGNO, is tested on a challenging suite of benchmarks, composed of various time-dependent and steady PDEs defined on a diverse set of domains. We demonstrate that RIGNO is significantly more accurate than neural operator baselines and robustly generalizes to unseen spatial resolutions and time instances.