Automated Constitutive Model Discovery by Pairing Sparse Regression Algorithms with Model Selection Criteria

The automated discovery of constitutive models from data has recently emerged as a promising alternative to the traditional model calibration paradigm. In this work, we present a fully automated framework for constitutive model discovery that systematically pairs three sparse regression algorithms (Least Absolute Shrinkage and Selection Operator (LASSO), Least Angle Regression (LARS), and Orthogonal Matching Pursuit (OMP)) with three model selection criteria: $K$-fold cross-validation (CV), Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC). This pairing yields nine distinct algorithms for model discovery and enables a systematic exploration of the trade-off between sparsity, predictive performance, and computational cost. While LARS serves as an efficient path-based solver for the $\ell_1$-constrained problem, OMP is introduced as a tractable heuristic for $\ell_0$-regularized selection. The framework is applied to both isotropic and anisotropic hyperelasticity, utilizing both synthetic and experimental datasets. Results reveal that all nine algorithm-criterion combinations perform consistently well for the discovery of isotropic and anisotropic materials, yielding highly accurate constitutive models. These findings broaden the range of viable discovery algorithms beyond $\ell_1$-based approaches such as LASSO.

A review on data-driven constitutive laws for solids

This review article highlights state-of-the-art data-driven techniques to discover, encode, surrogate, or emulate constitutive laws that describe the path-independent and path-dependent response of solids. Our objective is to provide an organized taxonomy to a large spectrum of methodologies developed in the past decades and to discuss the benefits and drawbacks of the various techniques for interpreting and forecasting mechanics behavior across different scales. Distinguishing between machine-learning-based and model-free methods, we further categorize approaches based on their interpretability and on their learning process/type of required data, while discussing the key problems of generalization and trustworthiness. We attempt to provide a road map of how these can be reconciled in a data-availability-aware context. We also touch upon relevant aspects such as data sampling techniques, design of experiments, verification, and validation.

NN-EUCLID: deep-learning hyperelasticity without stress data

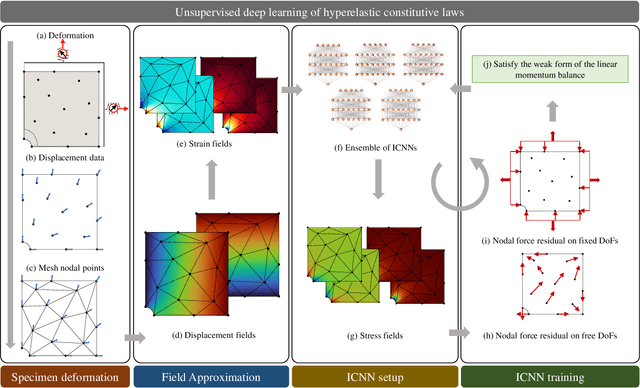
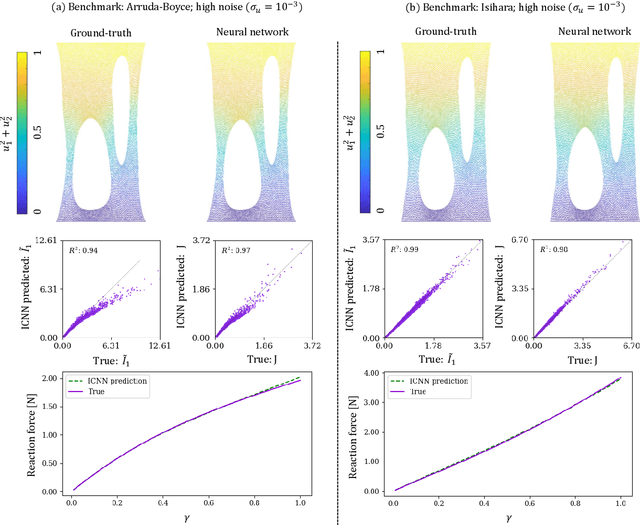
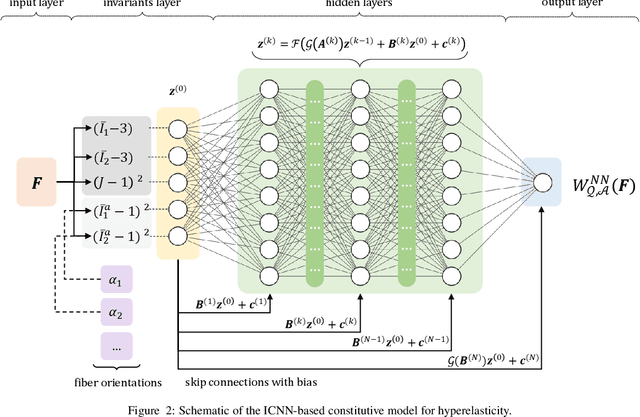
We propose a new approach for unsupervised learning of hyperelastic constitutive laws with physics-consistent deep neural networks. In contrast to supervised learning, which assumes the availability of stress-strain pairs, the approach only uses realistically measurable full-field displacement and global reaction force data, thus it lies within the scope of our recent framework for Efficient Unsupervised Constitutive Law Identification and Discovery (EUCLID) and we denote it as NN-EUCLID. The absence of stress labels is compensated for by leveraging a physics-motivated loss function based on the conservation of linear momentum to guide the learning process. The constitutive model is based on input-convex neural networks, which are capable of learning a function that is convex with respect to its inputs. By employing a specially designed neural network architecture, multiple physical and thermodynamic constraints for hyperelastic constitutive laws, such as material frame indifference, (poly-)convexity, and stress-free reference configuration are automatically satisfied. We demonstrate the ability of the approach to accurately learn several hidden isotropic and anisotropic hyperelastic constitutive laws - including e.g., Mooney-Rivlin, Arruda-Boyce, Ogden, and Holzapfel models - without using stress data. For anisotropic hyperelasticity, the unknown anisotropic fiber directions are automatically discovered jointly with the constitutive model. The neural network-based constitutive models show good generalization capability beyond the strain states observed during training and are readily deployable in a general finite element framework for simulating complex mechanical boundary value problems with good accuracy.