Improving the performance of Stein variational inference through extreme sparsification of physically-constrained neural network models

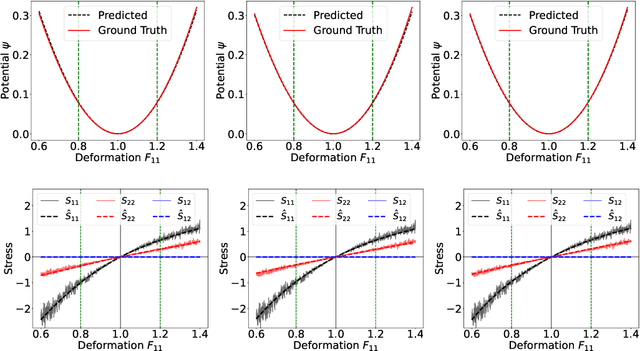
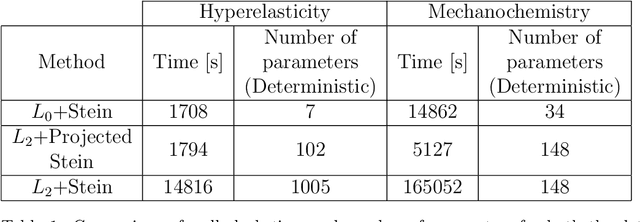
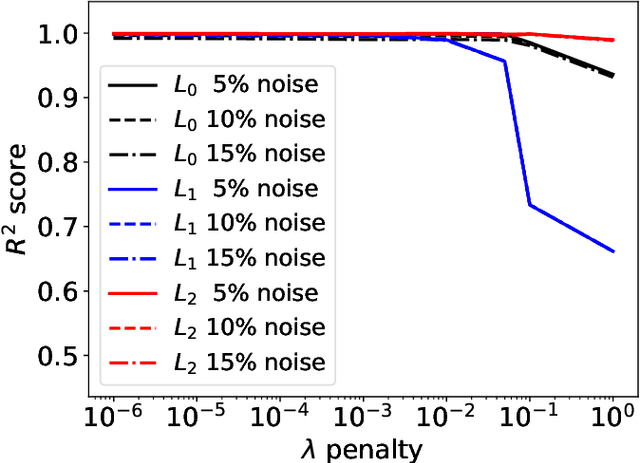
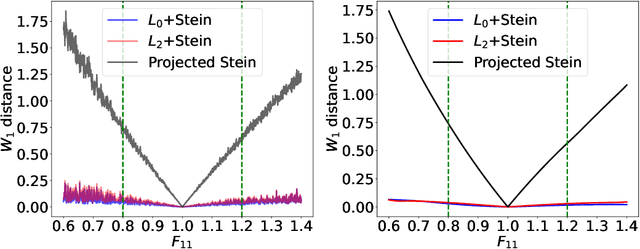
Most scientific machine learning (SciML) applications of neural networks involve hundreds to thousands of parameters, and hence, uncertainty quantification for such models is plagued by the curse of dimensionality. Using physical applications, we show that $L_0$ sparsification prior to Stein variational gradient descent ($L_0$+SVGD) is a more robust and efficient means of uncertainty quantification, in terms of computational cost and performance than the direct application of SGVD or projected SGVD methods. Specifically, $L_0$+SVGD demonstrates superior resilience to noise, the ability to perform well in extrapolated regions, and a faster convergence rate to an optimal solution.

A review on data-driven constitutive laws for solids

This review article highlights state-of-the-art data-driven techniques to discover, encode, surrogate, or emulate constitutive laws that describe the path-independent and path-dependent response of solids. Our objective is to provide an organized taxonomy to a large spectrum of methodologies developed in the past decades and to discuss the benefits and drawbacks of the various techniques for interpreting and forecasting mechanics behavior across different scales. Distinguishing between machine-learning-based and model-free methods, we further categorize approaches based on their interpretability and on their learning process/type of required data, while discussing the key problems of generalization and trustworthiness. We attempt to provide a road map of how these can be reconciled in a data-availability-aware context. We also touch upon relevant aspects such as data sampling techniques, design of experiments, verification, and validation.

Interval and fuzzy physics-informed neural networks for uncertain fields

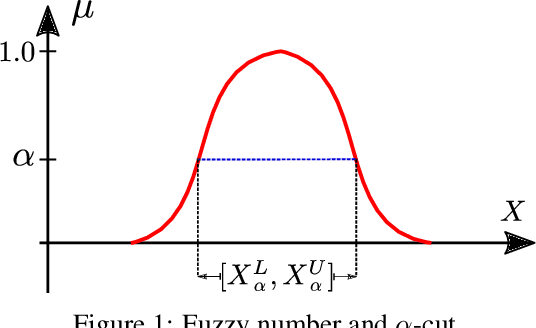
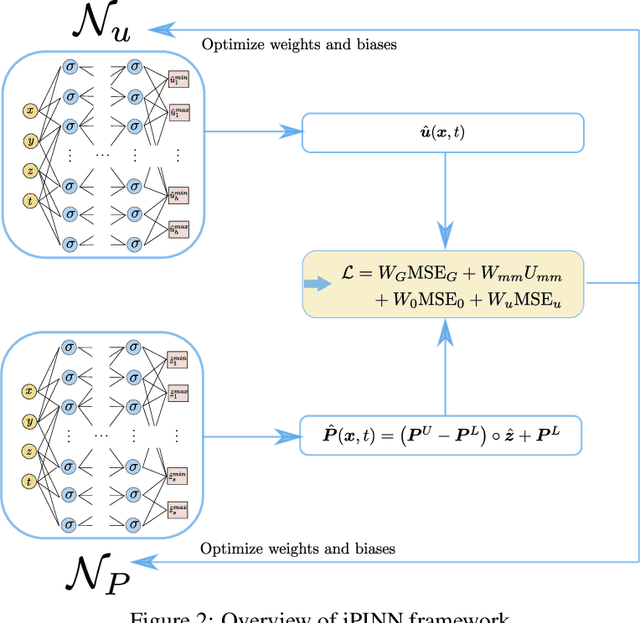
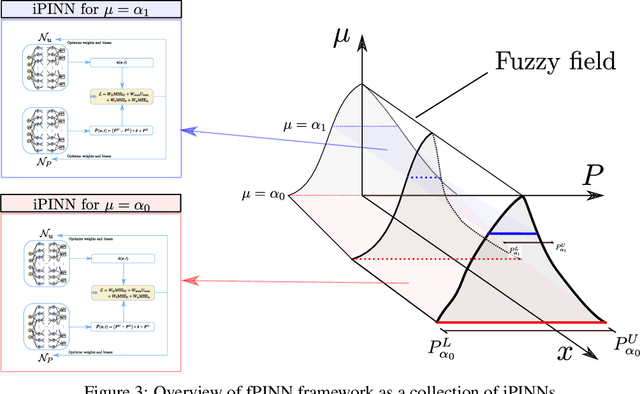
Temporally and spatially dependent uncertain parameters are regularly encountered in engineering applications. Commonly these uncertainties are accounted for using random fields and processes which require knowledge about the appearing probability distributions functions which is not readily available. In these cases non-probabilistic approaches such as interval analysis and fuzzy set theory are helpful uncertainty measures. Partial differential equations involving fuzzy and interval fields are traditionally solved using the finite element method where the input fields are sampled using some basis function expansion methods. This approach however is problematic, as it is reliant on knowledge about the spatial correlation fields. In this work we utilize physics-informed neural networks (PINNs) to solve interval and fuzzy partial differential equations. The resulting network structures termed interval physics-informed neural networks (iPINNs) and fuzzy physics-informed neural networks (fPINNs) show promising results for obtaining bounded solutions of equations involving spatially uncertain parameter fields. In contrast to finite element approaches, no correlation length specification of the input fields as well as no averaging via Monte-Carlo simulations are necessary. In fact, information about the input interval fields is obtained directly as a byproduct of the presented solution scheme. Furthermore, all major advantages of PINNs are retained, i.e. meshfree nature of the scheme, and ease of inverse problem set-up.

A framework for data-driven solution and parameter estimation of PDEs using conditional generative adversarial networks

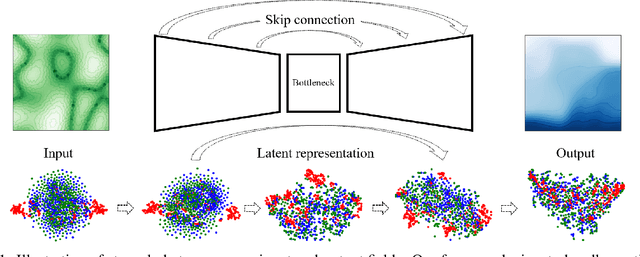
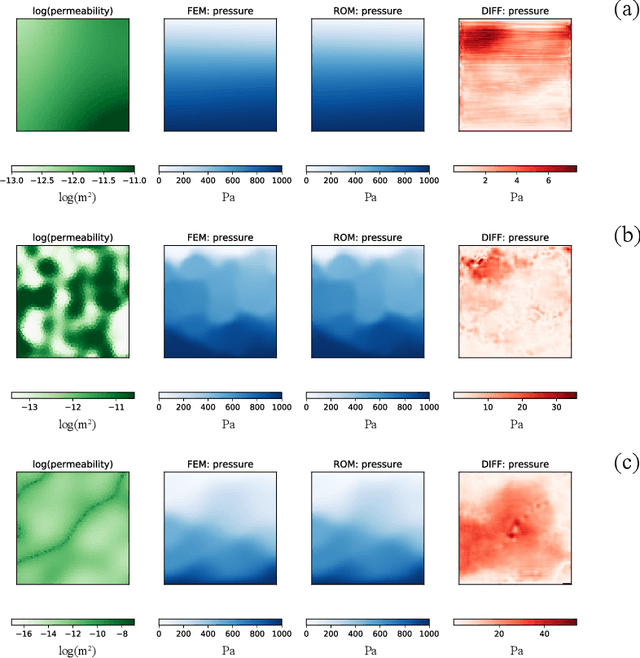
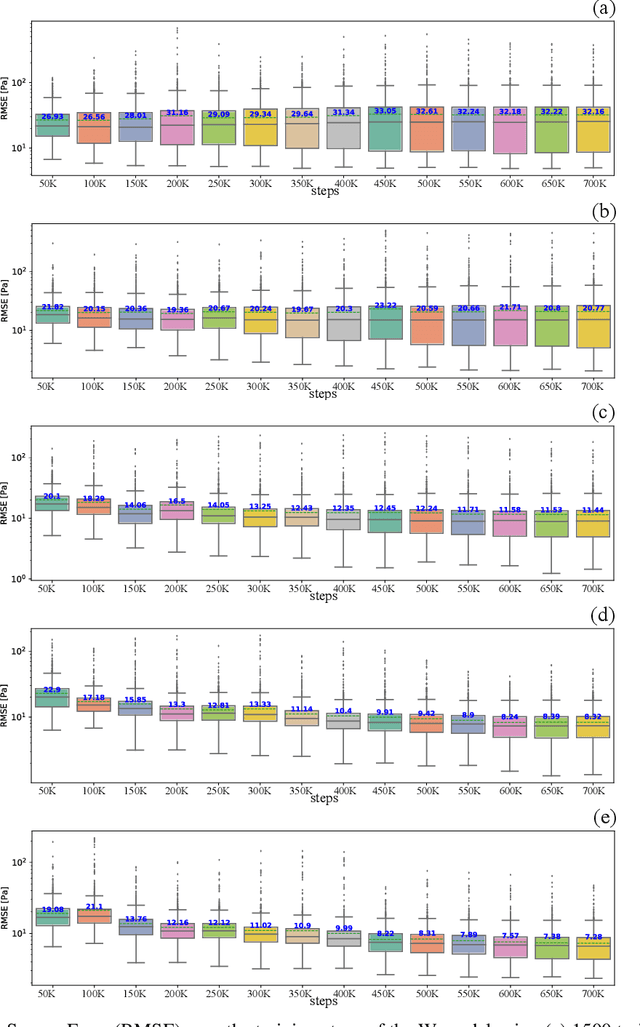
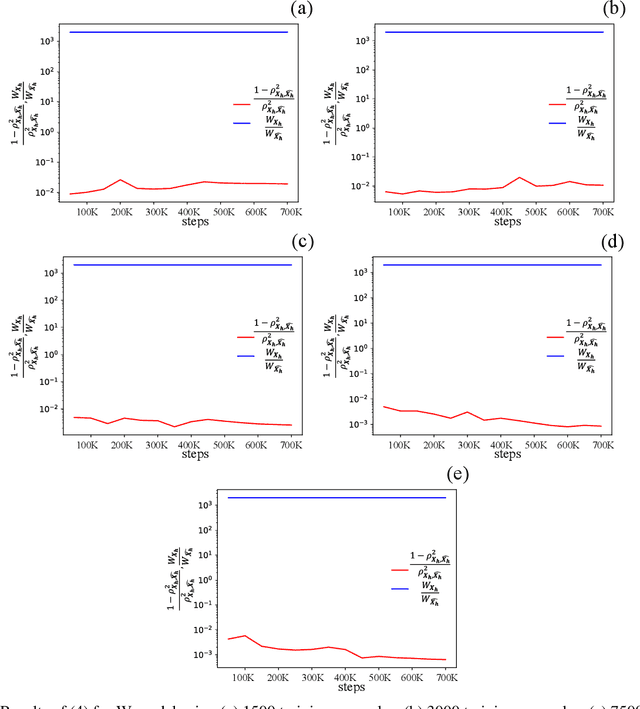
This work is the first to employ and adapt the image-to-image translation concept based on conditional generative adversarial networks (cGAN) towards learning a forward and an inverse solution operator of partial differential equations (PDEs). Even though the proposed framework could be applied as a surrogate model for the solution of any PDEs, here we focus on steady-state solutions of coupled hydro-mechanical processes in heterogeneous porous media. Strongly heterogeneous material properties, which translate to the heterogeneity of coefficients of the PDEs and discontinuous features in the solutions, require specialized techniques for the forward and inverse solution of these problems. Additionally, parametrization of the spatially heterogeneous coefficients is excessively difficult by using standard reduced order modeling techniques. In this work, we overcome these challenges by employing the image-to-image translation concept to learn the forward and inverse solution operators and utilize a U-Net generator and a patch-based discriminator. Our results show that the proposed data-driven reduced order model has competitive predictive performance capabilities in accuracy and computational efficiency as well as training time requirements compared to state-of-the-art data-driven methods for both forward and inverse problems.

Local approximate Gaussian process regression for data-driven constitutive laws: Development and comparison with neural networks

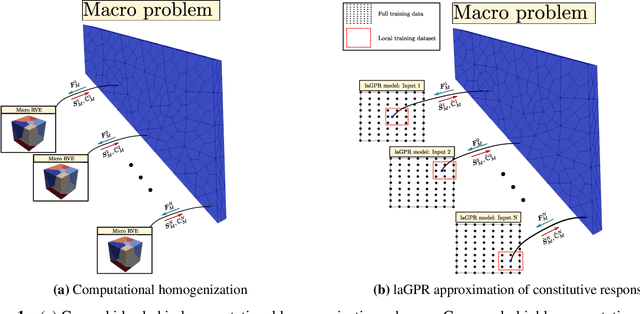
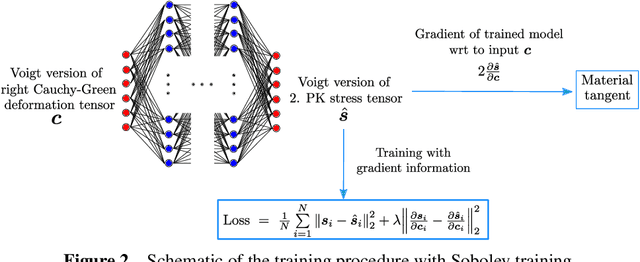
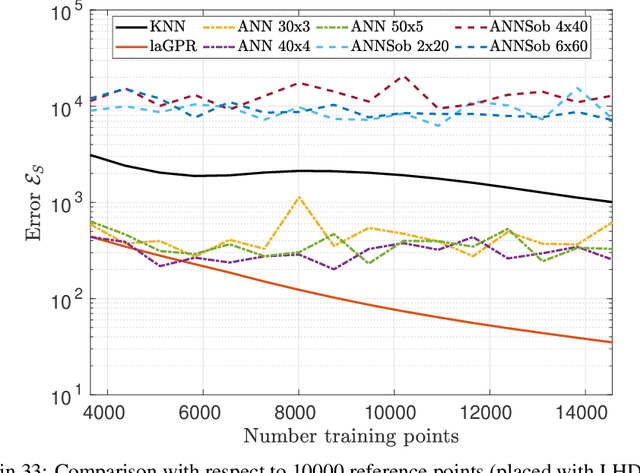
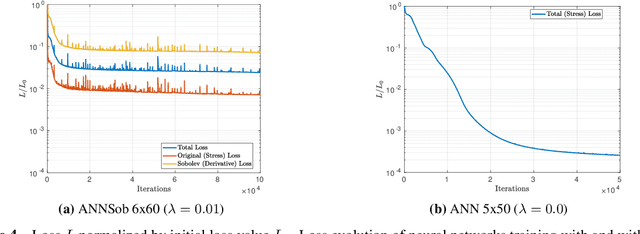
Hierarchical computational methods for multiscale mechanics such as the FE$^2$ and FE-FFT methods are generally accompanied by high computational costs. Data-driven approaches are able to speed the process up significantly by enabling to incorporate the effective micromechanical response in macroscale simulations without the need of performing additional computations at each Gauss point explicitly. Traditionally artificial neural networks (ANNs) have been the surrogate modeling technique of choice in the solid mechanics community. However they suffer from severe drawbacks due to their parametric nature and suboptimal training and inference properties for the investigated datasets in a three dimensional setting. These problems can be avoided using local approximate Gaussian process regression (laGPR). This method can allow the prediction of stress outputs at particular strain space locations by training local regression models based on Gaussian processes, using only a subset of the data for each local model, offering better and more reliable accuracy than ANNs. A modified Newton-Raphson approach is proposed to accommodate for the local nature of the laGPR approximation when solving the global structural problem in a FE setting. Hence, the presented work offers a complete and general framework enabling multiscale calculations combining a data-driven constitutive prediction using laGPR, and macroscopic calculations using an FE scheme that we test for finite-strain three-dimensional hyperelastic problems.

Model-data-driven constitutive responses: application to a multiscale computational framework

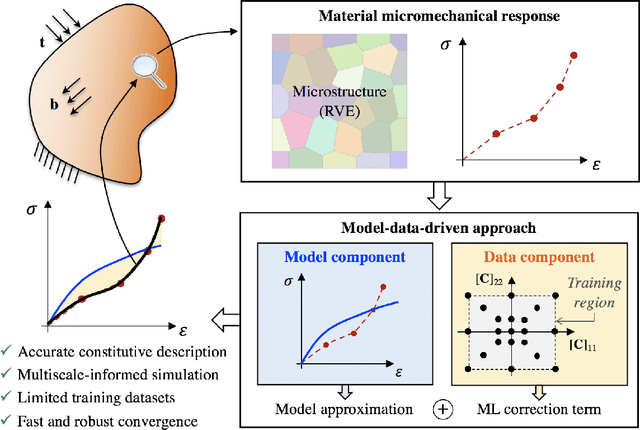
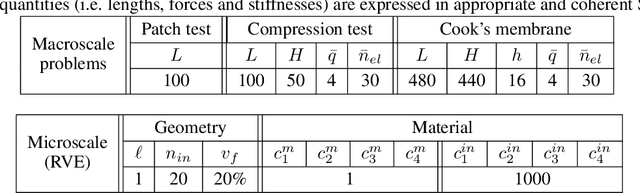
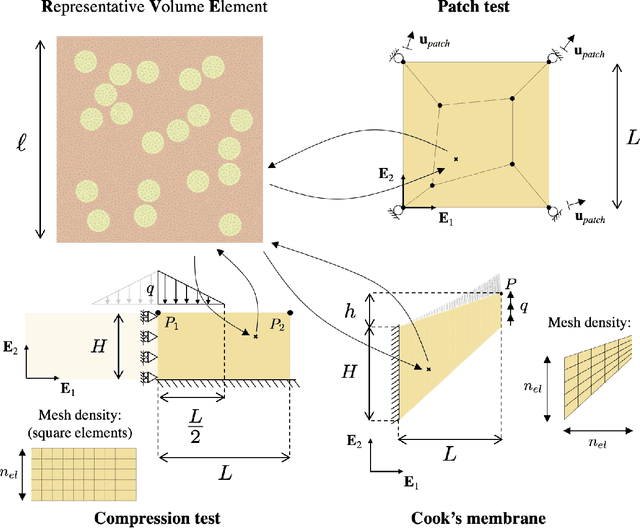
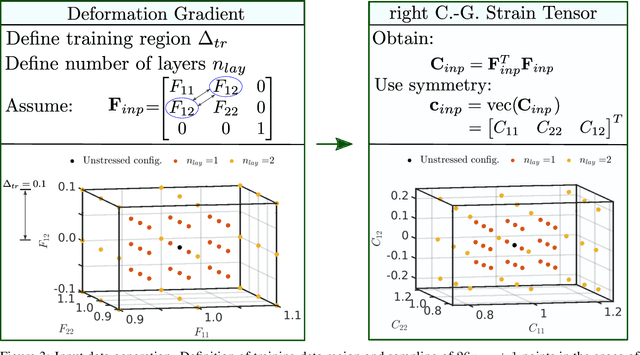
Computational multiscale methods for analyzing and deriving constitutive responses have been used as a tool in engineering problems because of their ability to combine information at different length scales. However, their application in a nonlinear framework can be limited by high computational costs, numerical difficulties, and/or inaccuracies. In this paper, a hybrid methodology is presented which combines classical constitutive laws (model-based), a data-driven correction component, and computational multiscale approaches. A model-based material representation is locally improved with data from lower scales obtained by means of a nonlinear numerical homogenization procedure leading to a model-data-driven approach. Therefore, macroscale simulations explicitly incorporate the true microscale response, maintaining the same level of accuracy that would be obtained with online micro-macro simulations but with a computational cost comparable to classical model-driven approaches. In the proposed approach, both model and data play a fundamental role allowing for the synergistic integration between a physics-based response and a machine learning black-box. Numerical applications are implemented in two dimensions for different tests investigating both material and structural responses in large deformation.

A machine learning based plasticity model using proper orthogonal decomposition

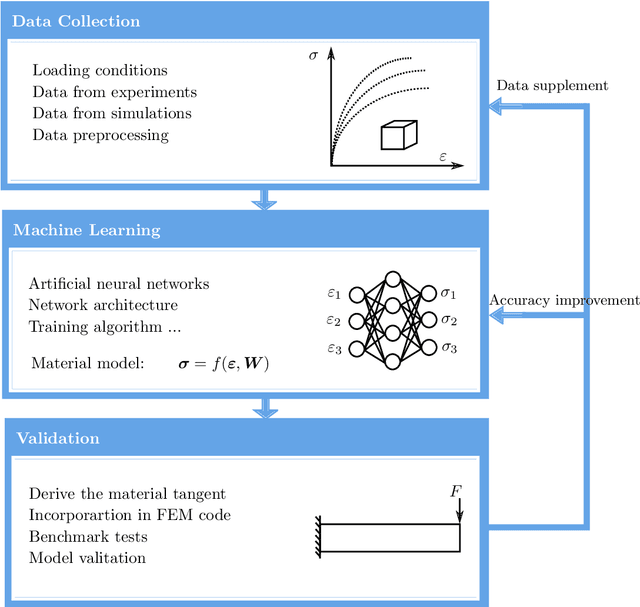
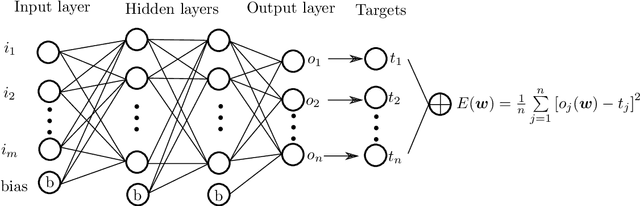
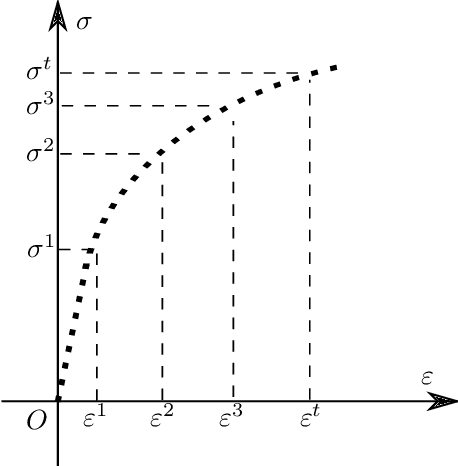
Data-driven material models have many advantages over classical numerical approaches, such as the direct utilization of experimental data and the possibility to improve performance of predictions when additional data is available. One approach to develop a data-driven material model is to use machine learning tools. These can be trained offline to fit an observed material behaviour and then be applied in online applications. However, learning and predicting history dependent material models, such as plasticity, is still challenging. In this work, a machine learning based material modelling framework is proposed for both elasticity and plasticity. The machine learning based hyperelasticity model is developed with the Feed forward Neural Network (FNN) directly whereas the machine learning based plasticity model is developed by using of a novel method called Proper Orthogonal Decomposition Feed forward Neural Network (PODFNN). In order to account for the loading history, the accumulated absolute strain is proposed to be the history variable of the plasticity model. Additionally, the strain-stress sequence data for plasticity is collected from different loading-unloading paths based on the concept of sequence for plasticity. By means of the POD, the multi-dimensional stress sequence is decoupled leading to independent one dimensional coefficient sequences. In this case, the neural network with multiple output is replaced by multiple independent neural networks each possessing a one-dimensional output, which leads to less training time and better training performance. To apply the machine learning based material model in finite element analysis, the tangent matrix is derived by the automatic symbolic differentiation tool AceGen. The effectiveness and generalization of the presented models are investigated by a series of numerical examples using both 2D and 3D finite element analysis.