Reese E. Jones
Uncertainty quantification of neural network models of evolving processes via Langevin sampling
Apr 21, 2025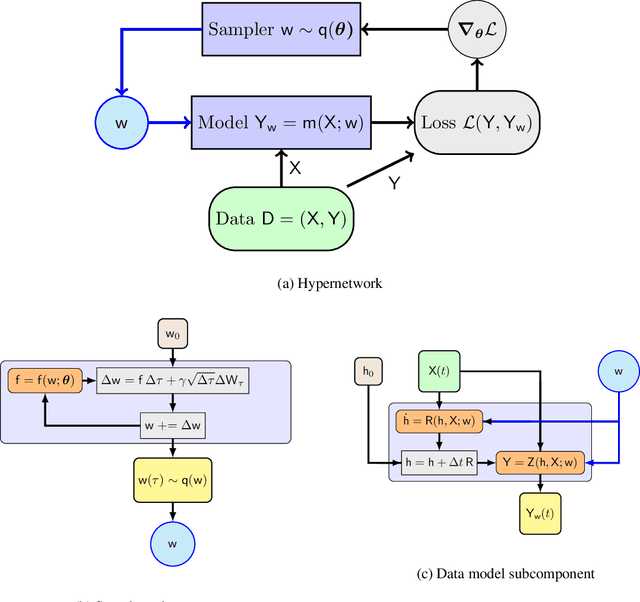
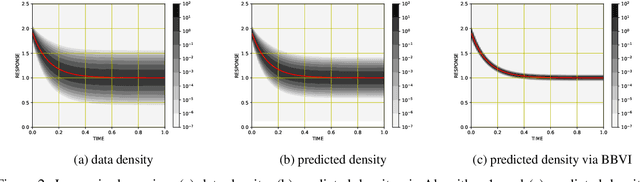
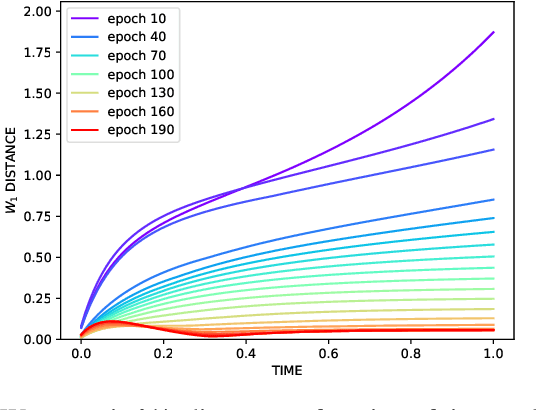
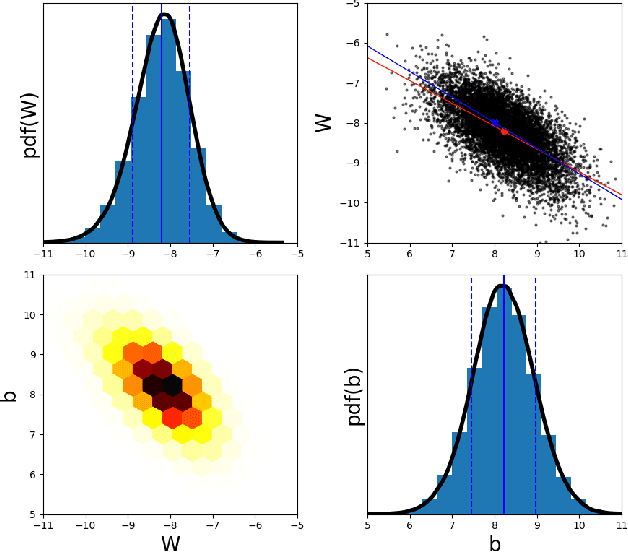
Abstract:We propose a scalable, approximate inference hypernetwork framework for a general model of history-dependent processes. The flexible data model is based on a neural ordinary differential equation (NODE) representing the evolution of internal states together with a trainable observation model subcomponent. The posterior distribution corresponding to the data model parameters (weights and biases) follows a stochastic differential equation with a drift term related to the score of the posterior that is learned jointly with the data model parameters. This Langevin sampling approach offers flexibility in balancing the computational budget between the evaluation cost of the data model and the approximation of the posterior density of its parameters. We demonstrate performance of the hypernetwork on chemical reaction and material physics data and compare it to mean-field variational inference.
Condensed Stein Variational Gradient Descent for Uncertainty Quantification of Neural Networks
Dec 21, 2024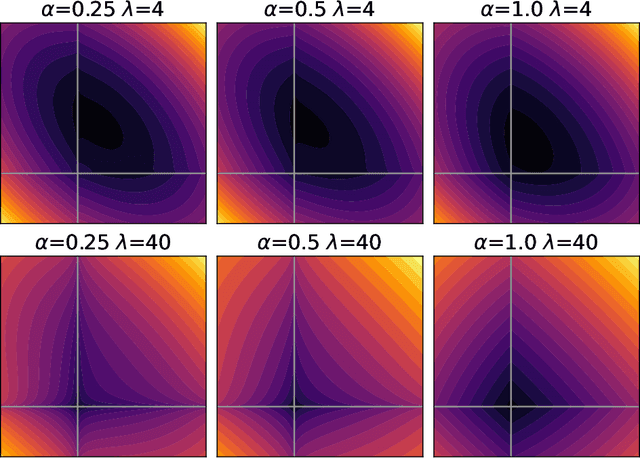
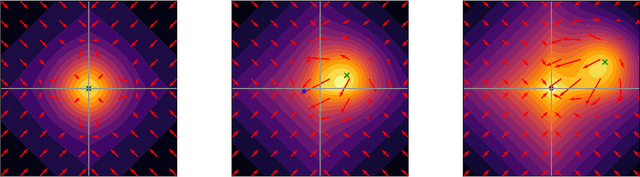
Abstract:We propose a Stein variational gradient descent method to concurrently sparsify, train, and provide uncertainty quantification of a complexly parameterized model such as a neural network. It employs a graph reconciliation and condensation process to reduce complexity and increase similarity in the Stein ensemble of parameterizations. Therefore, the proposed condensed Stein variational gradient (cSVGD) method provides uncertainty quantification on parameters, not just outputs. Furthermore, the parameter reduction speeds up the convergence of the Stein gradient descent as it reduces the combinatorial complexity by aligning and differentiating the sensitivity to parameters. These properties are demonstrated with an illustrative example and an application to a representation problem in solid mechanics.
Improving the performance of Stein variational inference through extreme sparsification of physically-constrained neural network models
Jun 30, 2024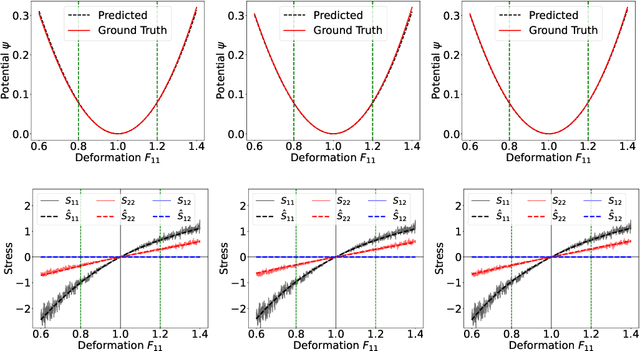
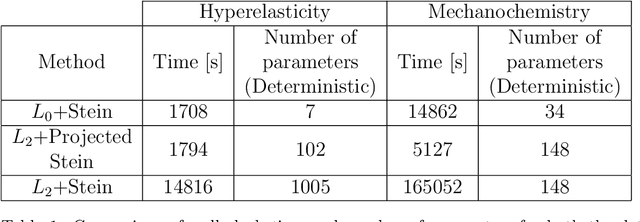
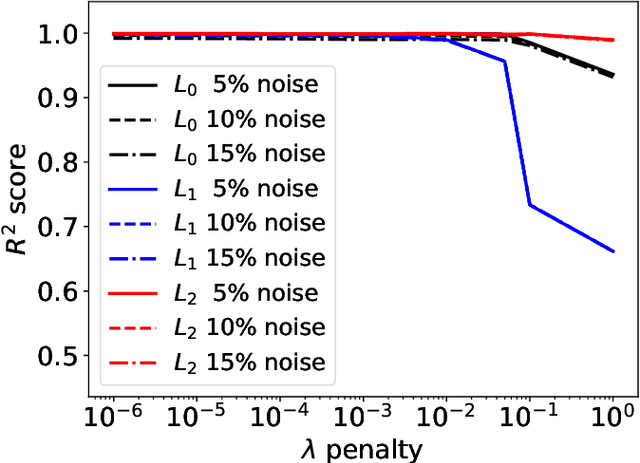
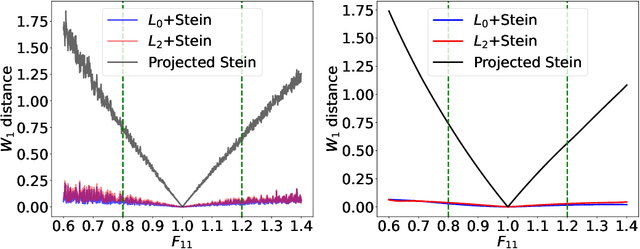
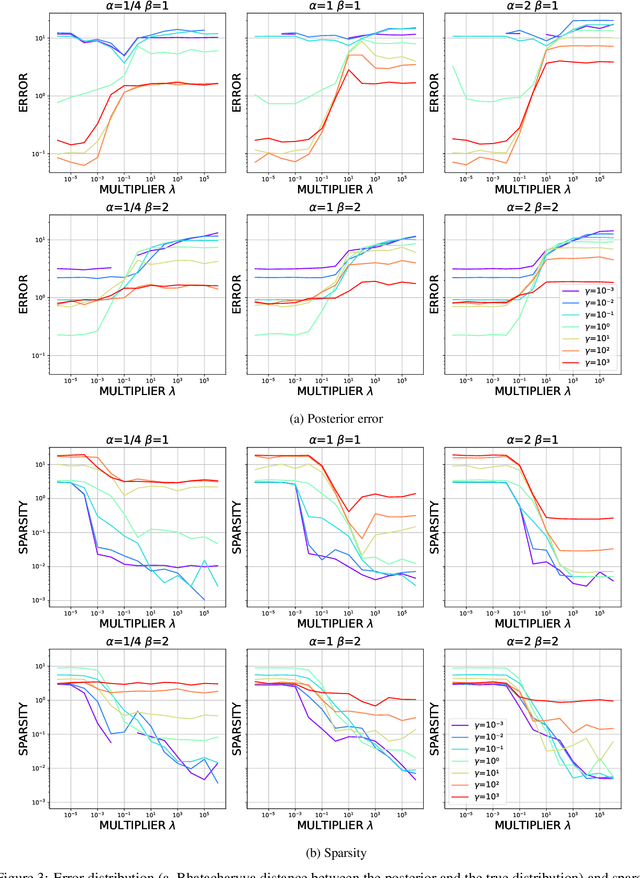
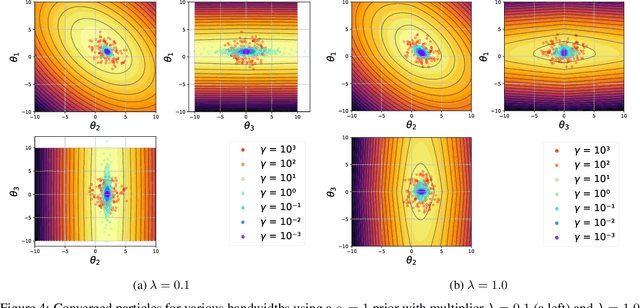
Abstract:Most scientific machine learning (SciML) applications of neural networks involve hundreds to thousands of parameters, and hence, uncertainty quantification for such models is plagued by the curse of dimensionality. Using physical applications, we show that $L_0$ sparsification prior to Stein variational gradient descent ($L_0$+SVGD) is a more robust and efficient means of uncertainty quantification, in terms of computational cost and performance than the direct application of SGVD or projected SGVD methods. Specifically, $L_0$+SVGD demonstrates superior resilience to noise, the ability to perform well in extrapolated regions, and a faster convergence rate to an optimal solution.
Uncertainty Quantification of Graph Convolution Neural Network Models of Evolving Processes
Feb 17, 2024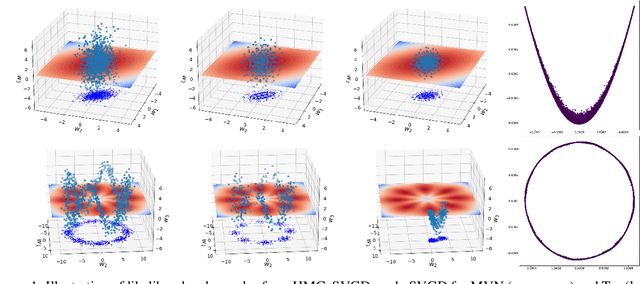
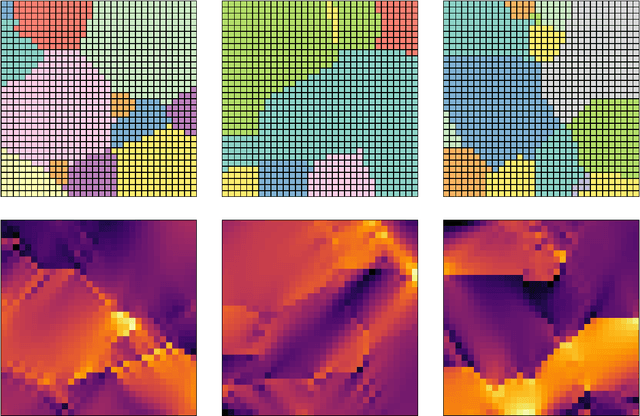
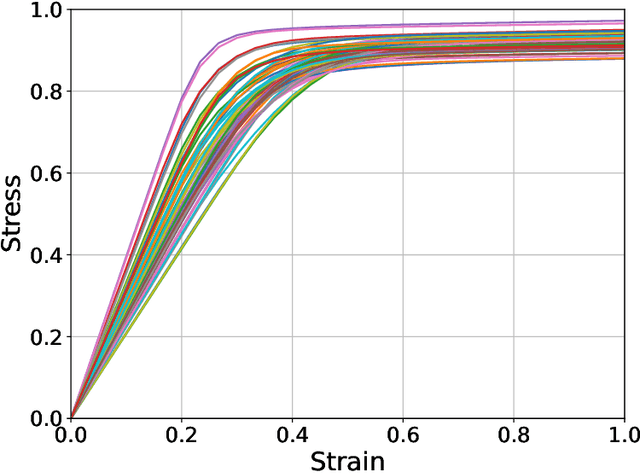
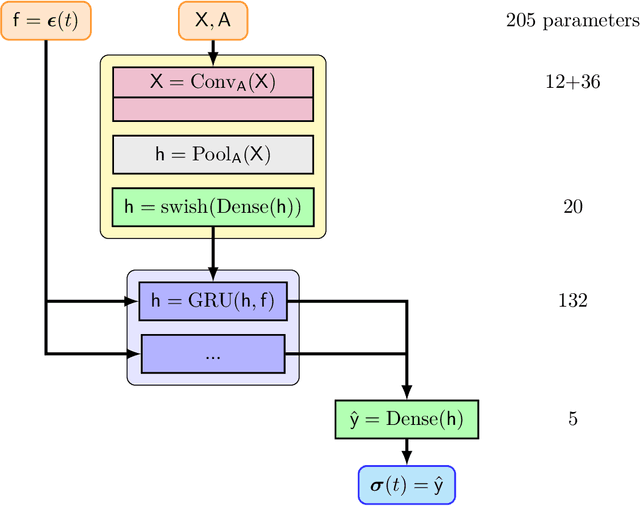
Abstract:The application of neural network models to scientific machine learning tasks has proliferated in recent years. In particular, neural network models have proved to be adept at modeling processes with spatial-temporal complexity. Nevertheless, these highly parameterized models have garnered skepticism in their ability to produce outputs with quantified error bounds over the regimes of interest. Hence there is a need to find uncertainty quantification methods that are suitable for neural networks. In this work we present comparisons of the parametric uncertainty quantification of neural networks modeling complex spatial-temporal processes with Hamiltonian Monte Carlo and Stein variational gradient descent and its projected variant. Specifically we apply these methods to graph convolutional neural network models of evolving systems modeled with recurrent neural network and neural ordinary differential equations architectures. We show that Stein variational inference is a viable alternative to Monte Carlo methods with some clear advantages for complex neural network models. For our exemplars, Stein variational interference gave similar uncertainty profiles through time compared to Hamiltonian Monte Carlo, albeit with generally more generous variance.Projected Stein variational gradient descent also produced similar uncertainty profiles to the non-projected counterpart, but large reductions in the active weight space were confounded by the stability of the neural network predictions and the convoluted likelihood landscape.
Accurate Data-Driven Surrogates of Dynamical Systems for Forward Propagation of Uncertainty
Oct 16, 2023Abstract:Stochastic collocation (SC) is a well-known non-intrusive method of constructing surrogate models for uncertainty quantification. In dynamical systems, SC is especially suited for full-field uncertainty propagation that characterizes the distributions of the high-dimensional primary solution fields of a model with stochastic input parameters. However, due to the highly nonlinear nature of the parameter-to-solution map in even the simplest dynamical systems, the constructed SC surrogates are often inaccurate. This work presents an alternative approach, where we apply the SC approximation over the dynamics of the model, rather than the solution. By combining the data-driven sparse identification of nonlinear dynamics (SINDy) framework with SC, we construct dynamics surrogates and integrate them through time to construct the surrogate solutions. We demonstrate that the SC-over-dynamics framework leads to smaller errors, both in terms of the approximated system trajectories as well as the model state distributions, when compared against full-field SC applied to the solutions directly. We present numerical evidence of this improvement using three test problems: a chaotic ordinary differential equation, and two partial differential equations from solid mechanics.
Extreme sparsification of physics-augmented neural networks for interpretable model discovery in mechanics
Oct 05, 2023Abstract:Data-driven constitutive modeling with neural networks has received increased interest in recent years due to its ability to easily incorporate physical and mechanistic constraints and to overcome the challenging and time-consuming task of formulating phenomenological constitutive laws that can accurately capture the observed material response. However, even though neural network-based constitutive laws have been shown to generalize proficiently, the generated representations are not easily interpretable due to their high number of trainable parameters. Sparse regression approaches exist that allow to obtaining interpretable expressions, but the user is tasked with creating a library of model forms which by construction limits their expressiveness to the functional forms provided in the libraries. In this work, we propose to train regularized physics-augmented neural network-based constitutive models utilizing a smoothed version of $L^{0}$-regularization. This aims to maintain the trustworthiness inherited by the physical constraints, but also enables interpretability which has not been possible thus far on any type of machine learning-based constitutive model where model forms were not assumed a-priory but were actually discovered. During the training process, the network simultaneously fits the training data and penalizes the number of active parameters, while also ensuring constitutive constraints such as thermodynamic consistency. We show that the method can reliably obtain interpretable and trustworthy constitutive models for compressible and incompressible hyperelasticity, yield functions, and hardening models for elastoplasticity, for synthetic and experimental data.
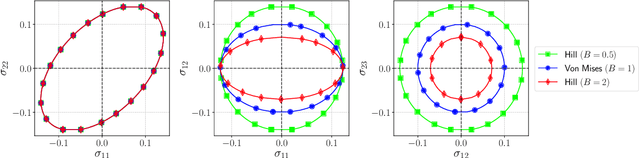
Stress representations for tensor basis neural networks: alternative formulations to Finger-Rivlin-Ericksen
Aug 21, 2023Abstract:Data-driven constitutive modeling frameworks based on neural networks and classical representation theorems have recently gained considerable attention due to their ability to easily incorporate constitutive constraints and their excellent generalization performance. In these models, the stress prediction follows from a linear combination of invariant-dependent coefficient functions and known tensor basis generators. However, thus far the formulations have been limited to stress representations based on the classical Rivlin and Ericksen form, while the performance of alternative representations has yet to be investigated. In this work, we survey a variety of tensor basis neural network models for modeling hyperelastic materials in a finite deformation context, including a number of so far unexplored formulations which use theoretically equivalent invariants and generators to Finger-Rivlin-Ericksen. Furthermore, we compare potential-based and coefficient-based approaches, as well as different calibration techniques. Nine variants are tested against both noisy and noiseless datasets for three different materials. Theoretical and practical insights into the performance of each formulation are given.
Design of experiments for the calibration of history-dependent models via deep reinforcement learning and an enhanced Kalman filter
Sep 27, 2022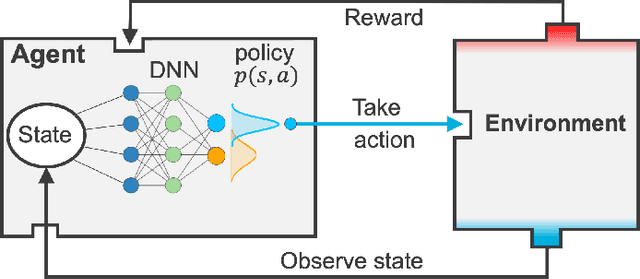

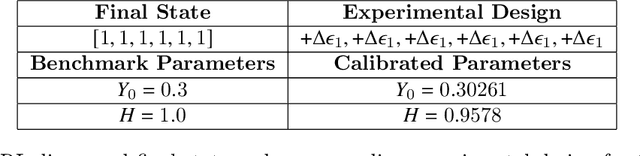
Abstract:Experimental data is costly to obtain, which makes it difficult to calibrate complex models. For many models an experimental design that produces the best calibration given a limited experimental budget is not obvious. This paper introduces a deep reinforcement learning (RL) algorithm for design of experiments that maximizes the information gain measured by Kullback-Leibler (KL) divergence obtained via the Kalman filter (KF). This combination enables experimental design for rapid online experiments where traditional methods are too costly. We formulate possible configurations of experiments as a decision tree and a Markov decision process (MDP), where a finite choice of actions is available at each incremental step. Once an action is taken, a variety of measurements are used to update the state of the experiment. This new data leads to a Bayesian update of the parameters by the KF, which is used to enhance the state representation. In contrast to the Nash-Sutcliffe efficiency (NSE) index, which requires additional sampling to test hypotheses for forward predictions, the KF can lower the cost of experiments by directly estimating the values of new data acquired through additional actions. In this work our applications focus on mechanical testing of materials. Numerical experiments with complex, history-dependent models are used to verify the implementation and benchmark the performance of the RL-designed experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge