Extreme sparsification of physics-augmented neural networks for interpretable model discovery in mechanics

Data-driven constitutive modeling with neural networks has received increased interest in recent years due to its ability to easily incorporate physical and mechanistic constraints and to overcome the challenging and time-consuming task of formulating phenomenological constitutive laws that can accurately capture the observed material response. However, even though neural network-based constitutive laws have been shown to generalize proficiently, the generated representations are not easily interpretable due to their high number of trainable parameters. Sparse regression approaches exist that allow to obtaining interpretable expressions, but the user is tasked with creating a library of model forms which by construction limits their expressiveness to the functional forms provided in the libraries. In this work, we propose to train regularized physics-augmented neural network-based constitutive models utilizing a smoothed version of $L^{0}$-regularization. This aims to maintain the trustworthiness inherited by the physical constraints, but also enables interpretability which has not been possible thus far on any type of machine learning-based constitutive model where model forms were not assumed a-priory but were actually discovered. During the training process, the network simultaneously fits the training data and penalizes the number of active parameters, while also ensuring constitutive constraints such as thermodynamic consistency. We show that the method can reliably obtain interpretable and trustworthy constitutive models for compressible and incompressible hyperelasticity, yield functions, and hardening models for elastoplasticity, for synthetic and experimental data.

Stress representations for tensor basis neural networks: alternative formulations to Finger-Rivlin-Ericksen

Data-driven constitutive modeling frameworks based on neural networks and classical representation theorems have recently gained considerable attention due to their ability to easily incorporate constitutive constraints and their excellent generalization performance. In these models, the stress prediction follows from a linear combination of invariant-dependent coefficient functions and known tensor basis generators. However, thus far the formulations have been limited to stress representations based on the classical Rivlin and Ericksen form, while the performance of alternative representations has yet to be investigated. In this work, we survey a variety of tensor basis neural network models for modeling hyperelastic materials in a finite deformation context, including a number of so far unexplored formulations which use theoretically equivalent invariants and generators to Finger-Rivlin-Ericksen. Furthermore, we compare potential-based and coefficient-based approaches, as well as different calibration techniques. Nine variants are tested against both noisy and noiseless datasets for three different materials. Theoretical and practical insights into the performance of each formulation are given.

Modular machine learning-based elastoplasticity: generalization in the context of limited data

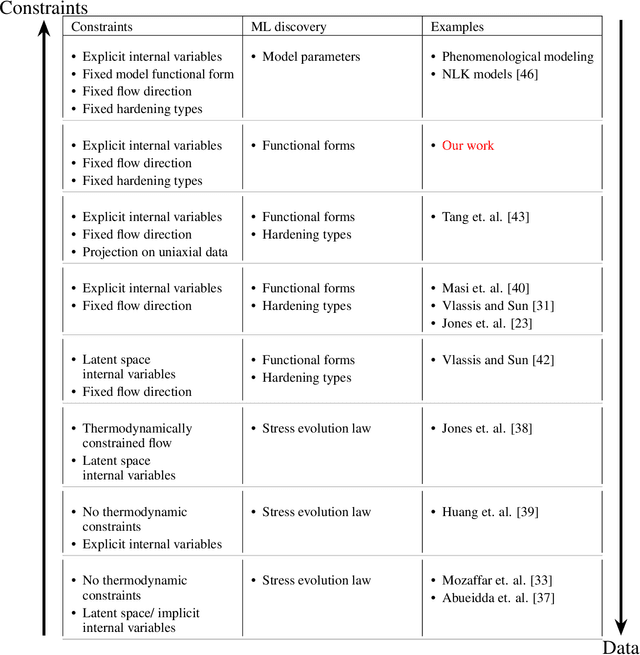
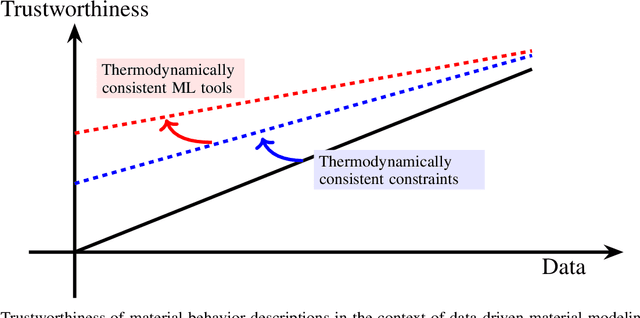
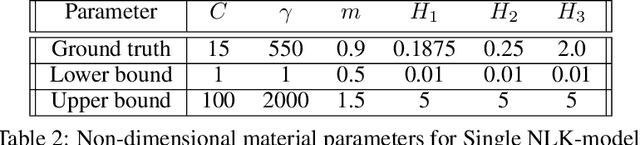
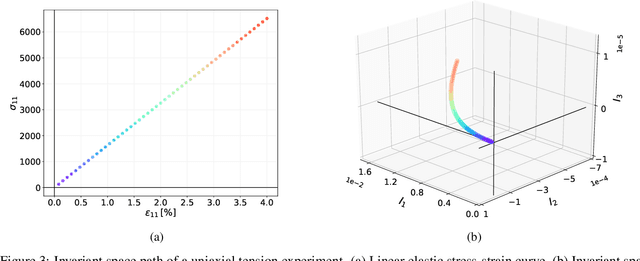
The development of accurate constitutive models for materials that undergo path-dependent processes continues to be a complex challenge in computational solid mechanics. Challenges arise both in considering the appropriate model assumptions and from the viewpoint of data availability, verification, and validation. Recently, data-driven modeling approaches have been proposed that aim to establish stress-evolution laws that avoid user-chosen functional forms by relying on machine learning representations and algorithms. However, these approaches not only require a significant amount of data but also need data that probes the full stress space with a variety of complex loading paths. Furthermore, they rarely enforce all necessary thermodynamic principles as hard constraints. Hence, they are in particular not suitable for low-data or limited-data regimes, where the first arises from the cost of obtaining the data and the latter from the experimental limitations of obtaining labeled data, which is commonly the case in engineering applications. In this work, we discuss a hybrid framework that can work on a variable amount of data by relying on the modularity of the elastoplasticity formulation where each component of the model can be chosen to be either a classical phenomenological or a data-driven model depending on the amount of available information and the complexity of the response. The method is tested on synthetic uniaxial data coming from simulations as well as cyclic experimental data for structural materials. The discovered material models are found to not only interpolate well but also allow for accurate extrapolation in a thermodynamically consistent manner far outside the domain of the training data. Training aspects and details of the implementation of these models into Finite Element simulations are discussed and analyzed.

The mixed deep energy method for resolving concentration features in finite strain hyperelasticity

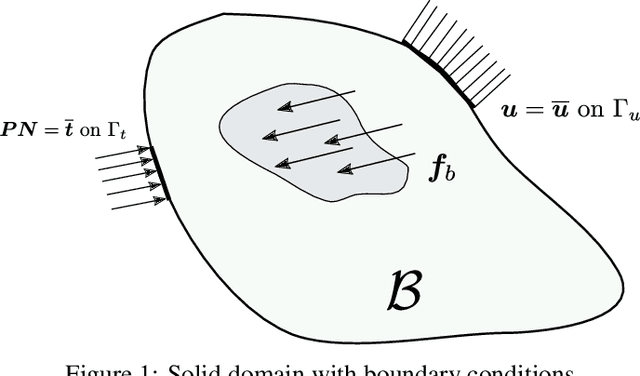
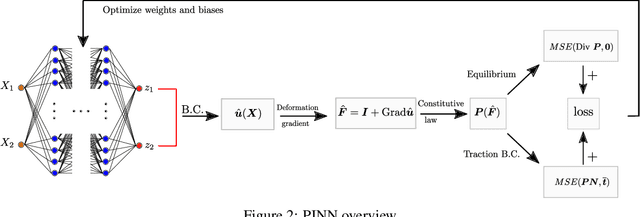
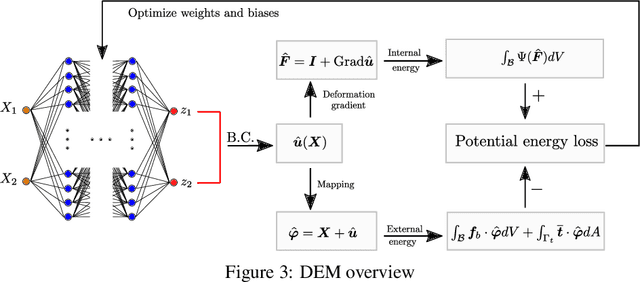
The introduction of Physics-informed Neural Networks (PINNs) has led to an increased interest in deep neural networks as universal approximators of PDEs in the solid mechanics community. Recently, the Deep Energy Method (DEM) has been proposed. DEM is based on energy minimization principles, contrary to PINN which is based on the residual of the PDEs. A significant advantage of DEM, is that it requires the approximation of lower order derivatives compared to formulations that are based on strong form residuals. However both DEM and classical PINN formulations struggle to resolve fine features of the stress and displacement fields, for example concentration features in solid mechanics applications. We propose an extension to the Deep Energy Method (DEM) to resolve these features for finite strain hyperelasticity. The developed framework termed mixed Deep Energy Method (mDEM) introduces stress measures as an additional output of the NN to the recently introduced pure displacement formulation. Using this approach, Neumann boundary conditions are approximated more accurately and the accuracy around spatial features which are typically responsible for high concentrations is increased. In order to make the proposed approach more versatile, we introduce a numerical integration scheme based on Delaunay integration, which enables the mDEM framework to be used for random training point position sets commonly needed for computational domains with stress concentrations. We highlight the advantages of the proposed approach while showing the shortcomings of classical PINN and DEM formulations. The method is offering comparable results to Finite-Element Method (FEM) on the forward calculation of challenging computational experiments involving domains with fine geometric features and concentrated loads.

An innovative adaptive kriging approach for efficient binary classification of mechanical problems

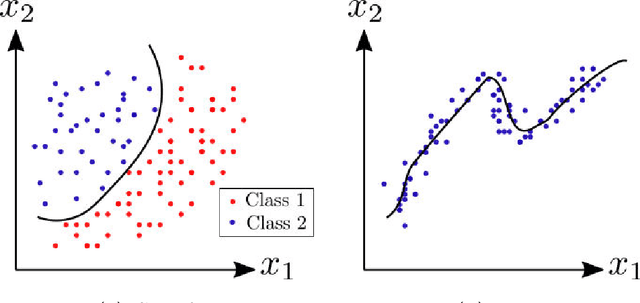
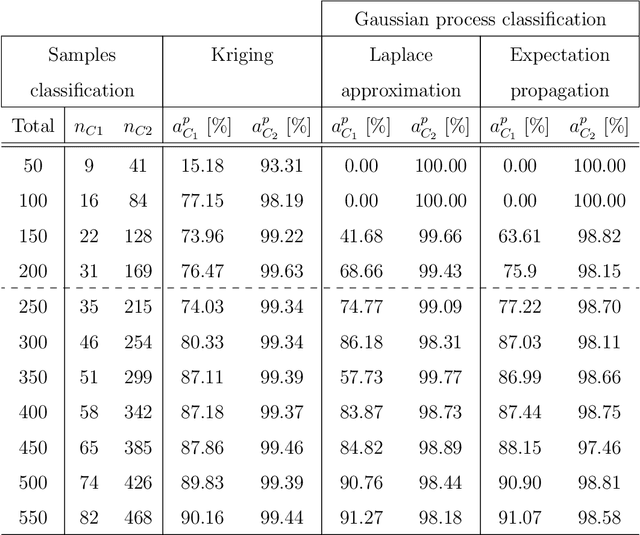
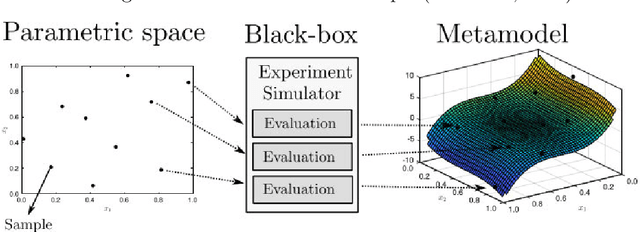
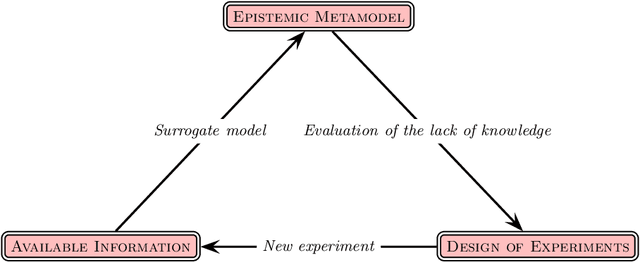
Kriging is an efficient machine-learning tool, which allows to obtain an approximate response of an investigated phenomenon on the whole parametric space. Adaptive schemes provide a the ability to guide the experiment yielding new sample point positions to enrich the metamodel. Herein a novel adaptive scheme called Monte Carlo-intersite Voronoi (MiVor) is proposed to efficiently identify binary decision regions on the basis of a regression surrogate model. The performance of the innovative approach is tested for analytical functions as well as some mechanical problems and is furthermore compared to two regression-based adaptive schemes. For smooth problems, all three methods have comparable performances. For highly fluctuating response surface as encountered e.g. for dynamics or damage problems, the innovative MiVor algorithm performs very well and provides accurate binary classification with only a few observation points.

Adaptive surrogate models for parametric studies

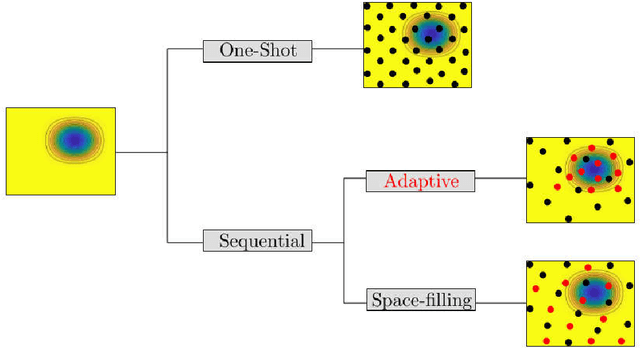
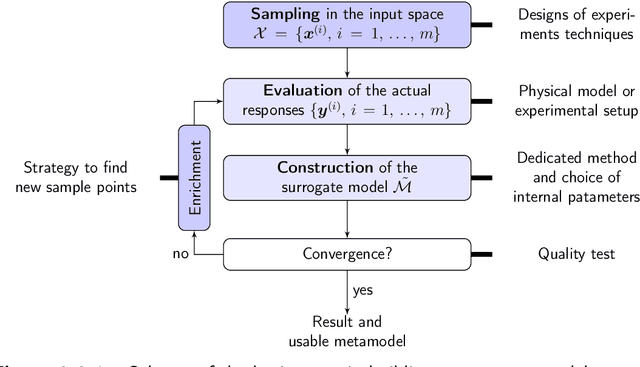
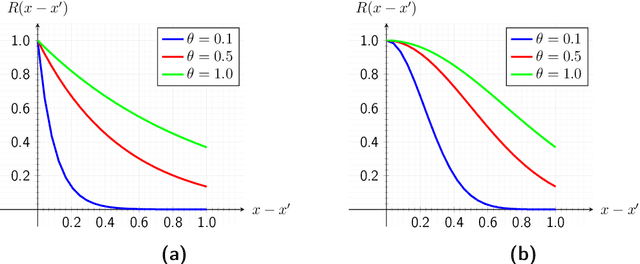
The computational effort for the evaluation of numerical simulations based on e.g. the finite-element method is high. Metamodels can be utilized to create a low-cost alternative. However the number of required samples for the creation of a sufficient metamodel should be kept low, which can be achieved by using adaptive sampling techniques. In this Master thesis adaptive sampling techniques are investigated for their use in creating metamodels with the Kriging technique, which interpolates values by a Gaussian process governed by prior covariances. The Kriging framework with extension to multifidelity problems is presented and utilized to compare adaptive sampling techniques found in the literature for benchmark problems as well as applications for contact mechanics. This thesis offers the first comprehensive comparison of a large spectrum of adaptive techniques for the Kriging framework. Furthermore a multitude of adaptive techniques is introduced to multifidelity Kriging as well as well as to a Kriging model with reduced hyperparameter dimension called partial least squares Kriging. In addition, an innovative adaptive scheme for binary classification is presented and tested for identifying chaotic motion of a Duffing's type oscillator.