Enhancing Polynomial Chaos Expansion Based Surrogate Modeling using a Novel Probabilistic Transfer Learning Strategy

In the field of surrogate modeling, polynomial chaos expansion (PCE) allows practitioners to construct inexpensive yet accurate surrogates to be used in place of the expensive forward model simulations. For black-box simulations, non-intrusive PCE allows the construction of these surrogates using a set of simulation response evaluations. In this context, the PCE coefficients can be obtained using linear regression, which is also known as point collocation or stochastic response surfaces. Regression exhibits better scalability and can handle noisy function evaluations in contrast to other non-intrusive approaches, such as projection. However, since over-sampling is generally advisable for the linear regression approach, the simulation requirements become prohibitive for expensive forward models. We propose to leverage transfer learning whereby knowledge gained through similar PCE surrogate construction tasks (source domains) is transferred to a new surrogate-construction task (target domain) which has a limited number of forward model simulations (training data). The proposed transfer learning strategy determines how much, if any, information to transfer using new techniques inspired by Bayesian modeling and data assimilation. The strategy is scrutinized using numerical investigations and applied to an engineering problem from the oil and gas industry.

Robust scalable initialization for Bayesian variational inference with multi-modal Laplace approximations

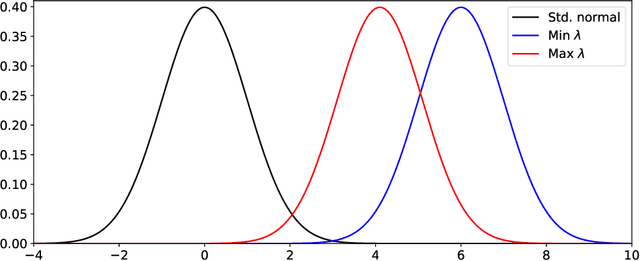
For predictive modeling relying on Bayesian inversion, fully independent, or ``mean-field'', Gaussian distributions are often used as approximate probability density functions in variational inference since the number of variational parameters is twice the number of unknown model parameters. The resulting diagonal covariance structure coupled with unimodal behavior can be too restrictive when dealing with highly non-Gaussian behavior, including multimodality. High-fidelity surrogate posteriors in the form of Gaussian mixtures can capture any distribution to an arbitrary degree of accuracy while maintaining some analytical tractability. Variational inference with Gaussian mixtures with full-covariance structures suffers from a quadratic growth in variational parameters with the number of model parameters. Coupled with the existence of multiple local minima due to nonconvex trends in the loss functions often associated with variational inference, these challenges motivate the need for robust initialization procedures to improve the performance and scalability of variational inference with mixture models. In this work, we propose a method for constructing an initial Gaussian mixture model approximation that can be used to warm-start the iterative solvers for variational inference. The procedure begins with an optimization stage in model parameter space in which local gradient-based optimization, globalized through multistart, is used to determine a set of local maxima, which we take to approximate the mixture component centers. Around each mode, a local Gaussian approximation is constructed via the Laplace method. Finally, the mixture weights are determined through constrained least squares regression. Robustness and scalability are demonstrated using synthetic tests. The methodology is applied to an inversion problem in structural dynamics involving unknown viscous damping coefficients.

Modular machine learning-based elastoplasticity: generalization in the context of limited data

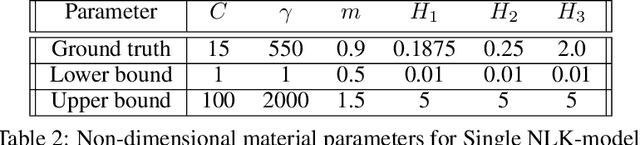
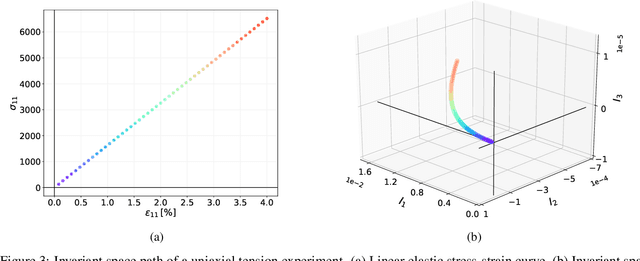
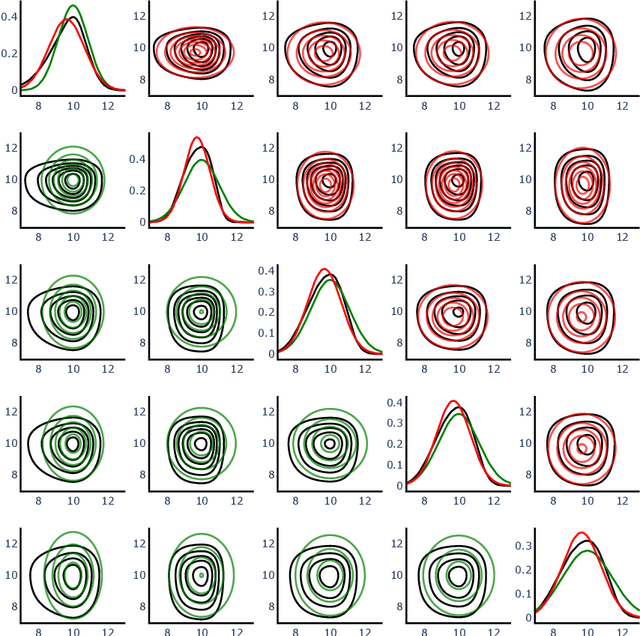
The development of accurate constitutive models for materials that undergo path-dependent processes continues to be a complex challenge in computational solid mechanics. Challenges arise both in considering the appropriate model assumptions and from the viewpoint of data availability, verification, and validation. Recently, data-driven modeling approaches have been proposed that aim to establish stress-evolution laws that avoid user-chosen functional forms by relying on machine learning representations and algorithms. However, these approaches not only require a significant amount of data but also need data that probes the full stress space with a variety of complex loading paths. Furthermore, they rarely enforce all necessary thermodynamic principles as hard constraints. Hence, they are in particular not suitable for low-data or limited-data regimes, where the first arises from the cost of obtaining the data and the latter from the experimental limitations of obtaining labeled data, which is commonly the case in engineering applications. In this work, we discuss a hybrid framework that can work on a variable amount of data by relying on the modularity of the elastoplasticity formulation where each component of the model can be chosen to be either a classical phenomenological or a data-driven model depending on the amount of available information and the complexity of the response. The method is tested on synthetic uniaxial data coming from simulations as well as cyclic experimental data for structural materials. The discovered material models are found to not only interpolate well but also allow for accurate extrapolation in a thermodynamically consistent manner far outside the domain of the training data. Training aspects and details of the implementation of these models into Finite Element simulations are discussed and analyzed.

Deep learning and multi-level featurization of graph representations of microstructural data

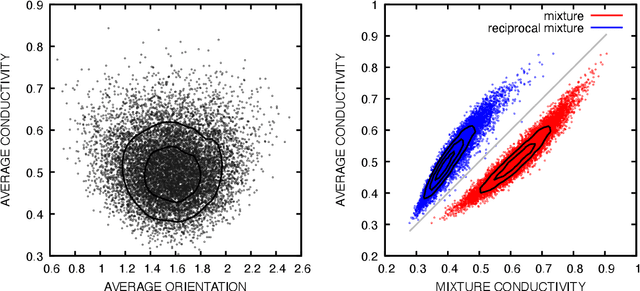
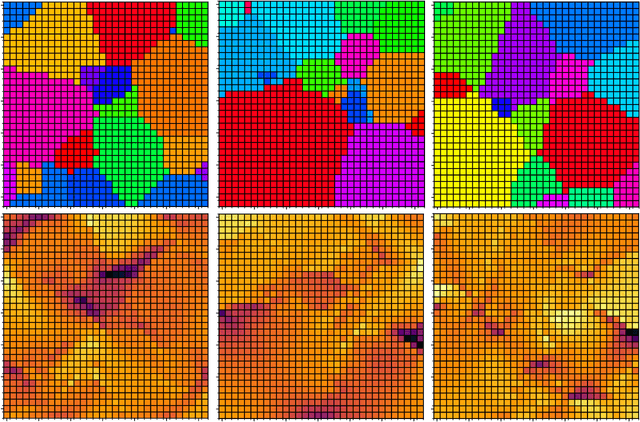
Many material response functions depend strongly on microstructure, such as inhomogeneities in phase or orientation. Homogenization presents the task of predicting the mean response of a sample of the microstructure to external loading for use in subgrid models and structure-property explorations. Although many microstructural fields have obvious segmentations, learning directly from the graph induced by the segmentation can be difficult because this representation does not encode all the information of the full field. We develop a means of deep learning of hidden features on the reduced graph given the native discretization and a segmentation of the initial input field. The features are associated with regions represented as nodes on the reduced graph. This reduced representation is then the basis for the subsequent multi-level/scale graph convolutional network model. There are a number of advantages of reducing the graph before fully processing with convolutional layers it, such as interpretable features and efficiency on large meshes. We demonstrate the performance of the proposed network relative to convolutional neural networks operating directly on the native discretization of the data using three physical exemplars.

A heteroencoder architecture for prediction of failure locations in porous metals using variational inference

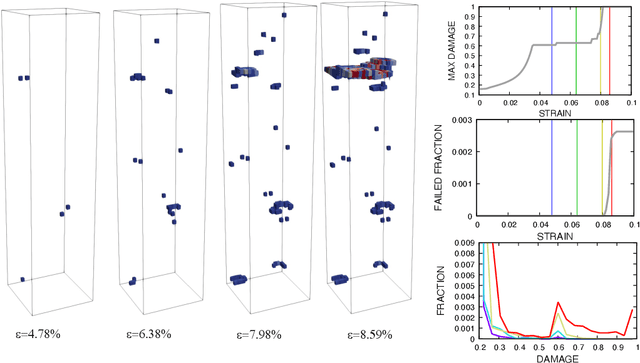
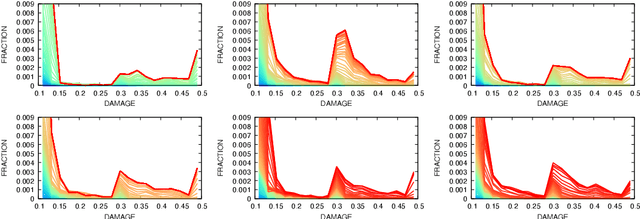
In this work we employ an encoder-decoder convolutional neural network to predict the failure locations of porous metal tension specimens based only on their initial porosities. The process we model is complex, with a progression from initial void nucleation, to saturation, and ultimately failure. The objective of predicting failure locations presents an extreme case of class imbalance since most of the material in the specimens do not fail. In response to this challenge, we develop and demonstrate the effectiveness of data- and loss-based regularization methods. Since there is considerable sensitivity of the failure location to the particular configuration of voids, we also use variational inference to provide uncertainties for the neural network predictions. We connect the deterministic and Bayesian convolutional neural networks at a theoretical level to explain how variational inference regularizes the training and predictions. We demonstrate that the resulting predicted variances are effective in ranking the locations that are most likely to fail in any given specimen.

Tensor Basis Gaussian Process Models of Hyperelastic Materials

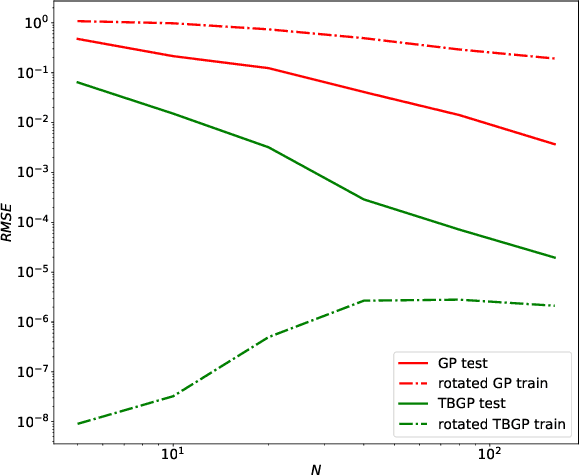
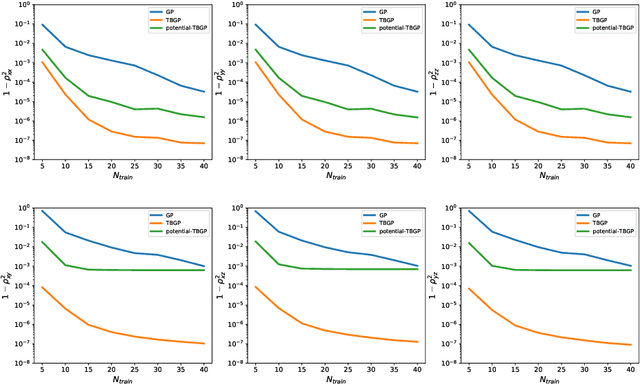
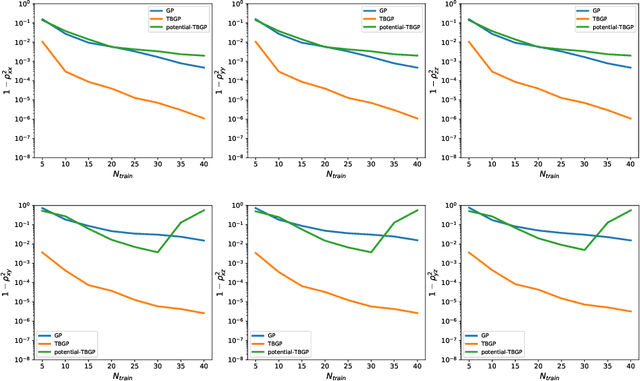
In this work, we develop Gaussian process regression (GPR) models of hyperelastic material behavior. First, we consider the direct approach of modeling the components of the Cauchy stress tensor as a function of the components of the Finger stretch tensor in a Gaussian process. We then consider an improvement on this approach that embeds rotational invariance of the stress-stretch constitutive relation in the GPR representation. This approach requires fewer training examples and achieves higher accuracy while maintaining invariance to rotations exactly. Finally, we consider an approach that recovers the strain-energy density function and derives the stress tensor from this potential. Although the error of this model for predicting the stress tensor is higher, the strain-energy density is recovered with high accuracy from limited training data. The approaches presented here are examples of physics-informed machine learning. They go beyond purely data-driven approaches by embedding the physical system constraints directly into the Gaussian process representation of materials models.