Uma Balakrishnan
Enhancing Polynomial Chaos Expansion Based Surrogate Modeling using a Novel Probabilistic Transfer Learning Strategy
Dec 07, 2023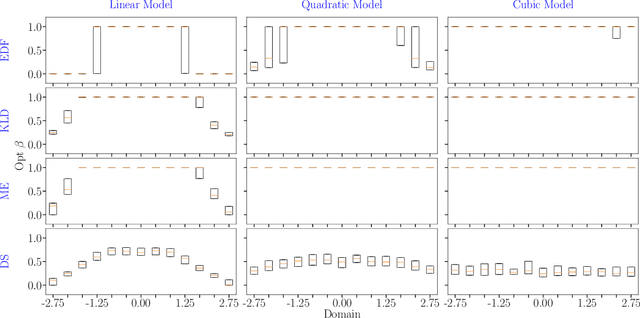
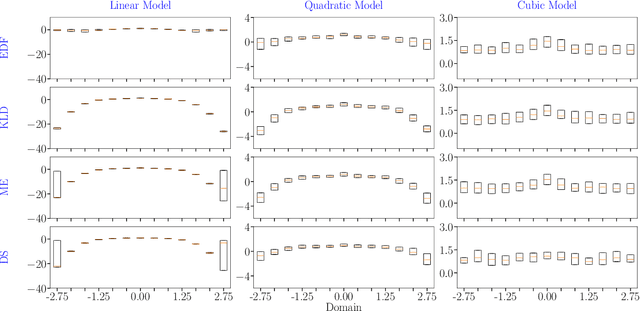
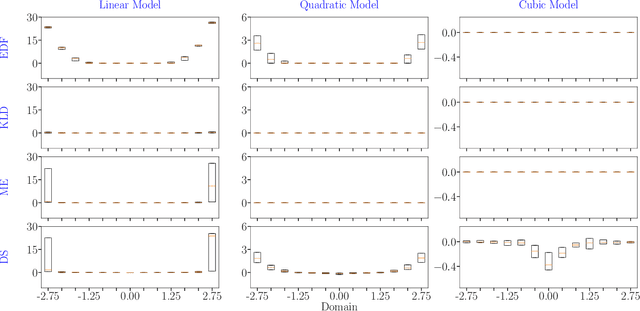
Abstract:In the field of surrogate modeling, polynomial chaos expansion (PCE) allows practitioners to construct inexpensive yet accurate surrogates to be used in place of the expensive forward model simulations. For black-box simulations, non-intrusive PCE allows the construction of these surrogates using a set of simulation response evaluations. In this context, the PCE coefficients can be obtained using linear regression, which is also known as point collocation or stochastic response surfaces. Regression exhibits better scalability and can handle noisy function evaluations in contrast to other non-intrusive approaches, such as projection. However, since over-sampling is generally advisable for the linear regression approach, the simulation requirements become prohibitive for expensive forward models. We propose to leverage transfer learning whereby knowledge gained through similar PCE surrogate construction tasks (source domains) is transferred to a new surrogate-construction task (target domain) which has a limited number of forward model simulations (training data). The proposed transfer learning strategy determines how much, if any, information to transfer using new techniques inspired by Bayesian modeling and data assimilation. The strategy is scrutinized using numerical investigations and applied to an engineering problem from the oil and gas industry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge