Cosmin Safta
Towards Spatio-Temporal Extrapolation of Phase-Field Simulations with Convolution-Only Neural Networks
Jan 08, 2026Abstract:Phase-field simulations of liquid metal dealloying (LMD) can capture complex microstructural evolutions but can be prohibitively expensive for large domains and long time horizons. In this paper, we introduce a fully convolutional, conditionally parameterized U-Net surrogate designed to extrapolate far beyond its training data in both space and time. The architecture integrates convolutional self-attention, physically informed padding, and a flood-fill corrector method to maintain accuracy under extreme extrapolation, while conditioning on simulation parameters allows for flexible time-step skipping and adaptation to varying alloy compositions. To remove the need for costly solver-based initialization, we couple the surrogate with a conditional diffusion model that generates synthetic, physically consistent initial conditions. We train our surrogate on simulations generated over small domain sizes and short time spans, but, by taking advantage of the convolutional nature of U-Nets, we are able to run and extrapolate surrogate simulations for longer time horizons than what would be achievable with classic numerical solvers. Across multiple alloy compositions, the framework is able to reproduce the LMD physics accurately. It predicts key quantities of interest and spatial statistics with relative errors typically below 5% in the training regime and under 15% during large-scale, long time-horizon extrapolations. Our framework can also deliver speed-ups of up to 36,000 times, bringing the time to run weeks-long simulations down to a few seconds. This work is a first stepping stone towards high-fidelity extrapolation in both space and time of phase-field simulation for LMD.
Uncertainty quantification of neural network models of evolving processes via Langevin sampling
Apr 21, 2025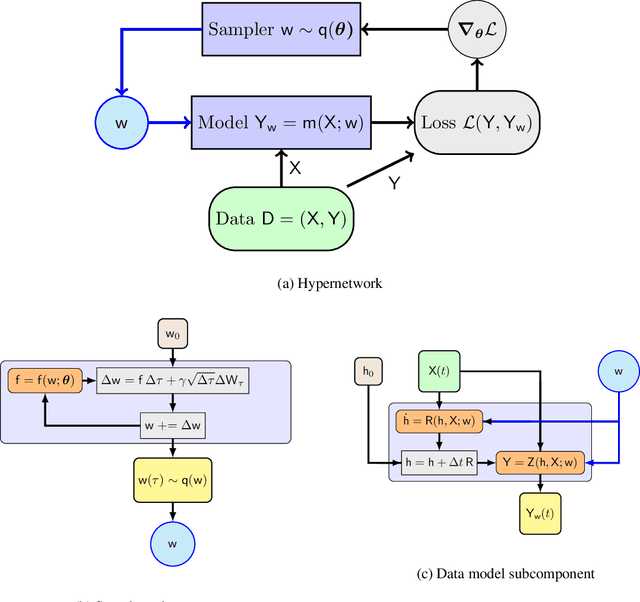
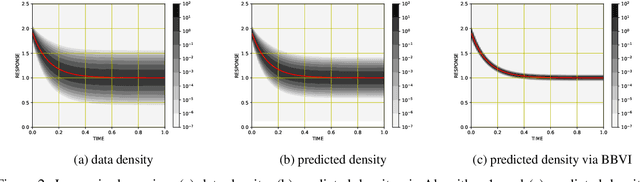
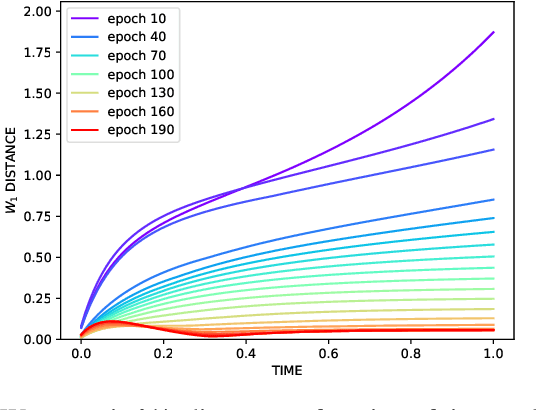
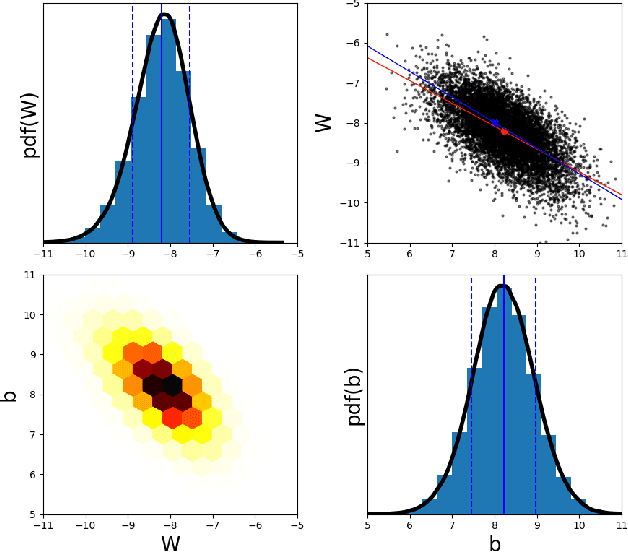
Abstract:We propose a scalable, approximate inference hypernetwork framework for a general model of history-dependent processes. The flexible data model is based on a neural ordinary differential equation (NODE) representing the evolution of internal states together with a trainable observation model subcomponent. The posterior distribution corresponding to the data model parameters (weights and biases) follows a stochastic differential equation with a drift term related to the score of the posterior that is learned jointly with the data model parameters. This Langevin sampling approach offers flexibility in balancing the computational budget between the evaluation cost of the data model and the approximation of the posterior density of its parameters. We demonstrate performance of the hypernetwork on chemical reaction and material physics data and compare it to mean-field variational inference.
Advancing calibration for stochastic agent-based models in epidemiology with Stein variational inference and Gaussian process surrogates
Feb 26, 2025
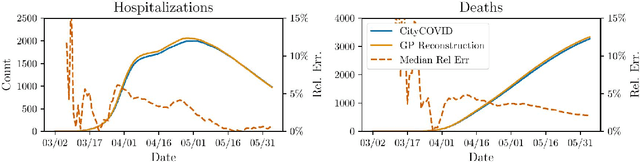
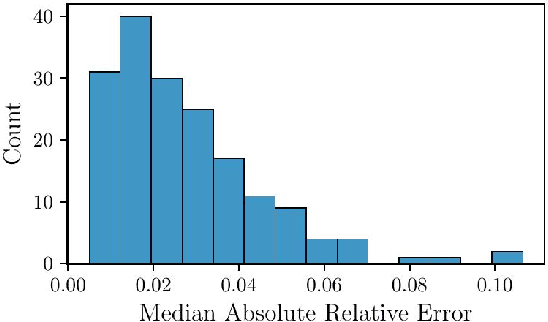

Abstract:Accurate calibration of stochastic agent-based models (ABMs) in epidemiology is crucial to make them useful in public health policy decisions and interventions. Traditional calibration methods, e.g., Markov Chain Monte Carlo (MCMC), that yield a probability density function for the parameters being calibrated, are often computationally expensive. When applied to ABMs which are highly parametrized, the calibration process becomes computationally infeasible. This paper investigates the utility of Stein Variational Inference (SVI) as an alternative calibration technique for stochastic epidemiological ABMs approximated by Gaussian process (GP) surrogates. SVI leverages gradient information to iteratively update a set of particles in the space of parameters being calibrated, offering potential advantages in scalability and efficiency for high-dimensional ABMs. The ensemble of particles yields a joint probability density function for the parameters and serves as the calibration. We compare the performance of SVI and MCMC in calibrating CityCOVID, a stochastic epidemiological ABM, focusing on predictive accuracy and calibration effectiveness. Our results demonstrate that SVI maintains predictive accuracy and calibration effectiveness comparable to MCMC, making it a viable alternative for complex epidemiological models. We also present the practical challenges of using a gradient-based calibration such as SVI which include careful tuning of hyperparameters and monitoring of the particle dynamics.
Condensed Stein Variational Gradient Descent for Uncertainty Quantification of Neural Networks
Dec 21, 2024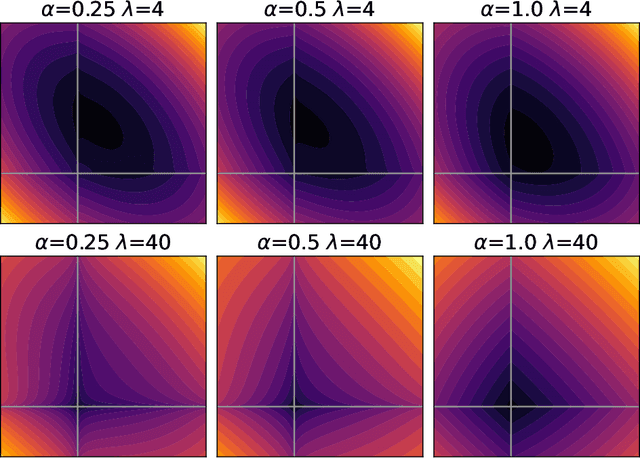
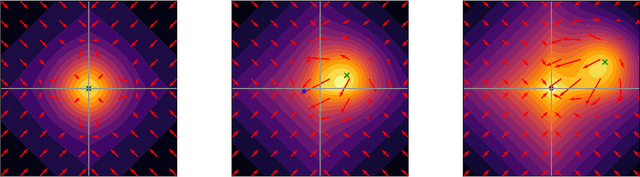
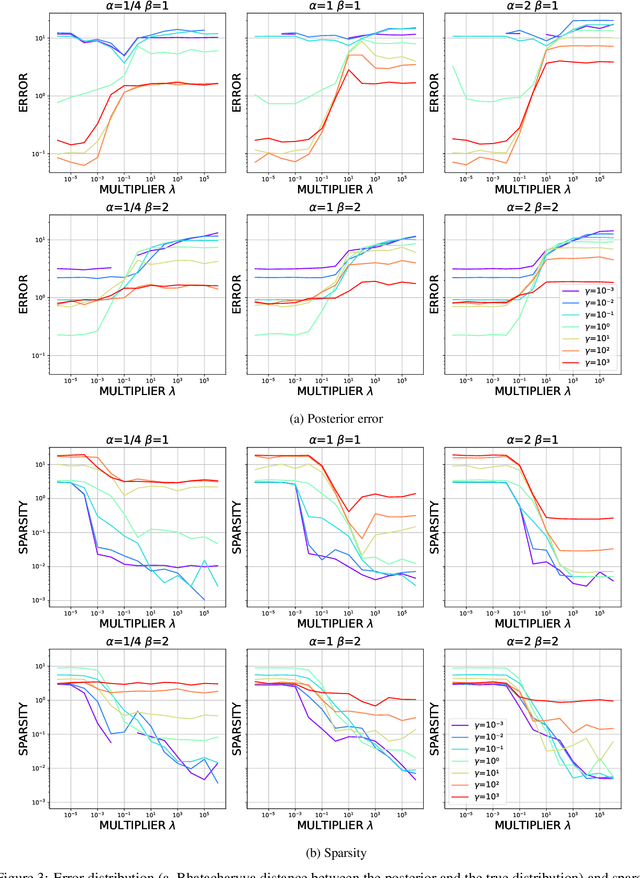
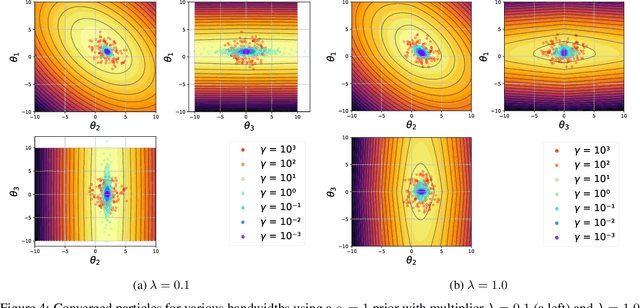
Abstract:We propose a Stein variational gradient descent method to concurrently sparsify, train, and provide uncertainty quantification of a complexly parameterized model such as a neural network. It employs a graph reconciliation and condensation process to reduce complexity and increase similarity in the Stein ensemble of parameterizations. Therefore, the proposed condensed Stein variational gradient (cSVGD) method provides uncertainty quantification on parameters, not just outputs. Furthermore, the parameter reduction speeds up the convergence of the Stein gradient descent as it reduces the combinatorial complexity by aligning and differentiating the sensitivity to parameters. These properties are demonstrated with an illustrative example and an application to a representation problem in solid mechanics.
A switching Kalman filter approach to online mitigation and correction sensor corruption for inertial navigation
Dec 09, 2024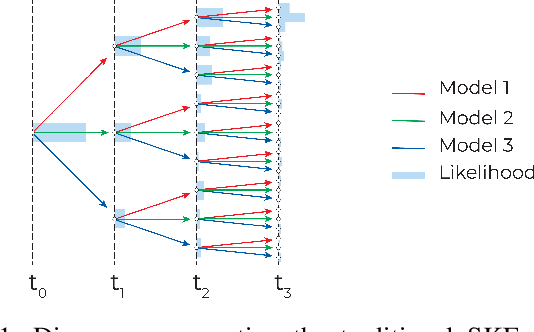
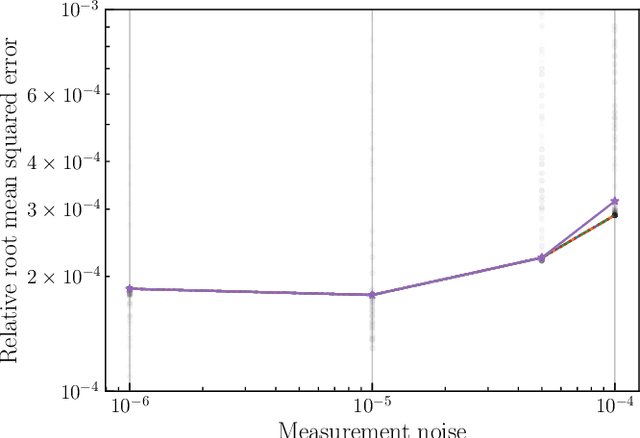
Abstract:This paper introduces a novel approach to detect and address faulty or corrupted external sensors in the context of inertial navigation by leveraging a switching Kalman Filter combined with parameter augmentation. Instead of discarding the corrupted data, the proposed method retains and processes it, running multiple observation models simultaneously and evaluating their likelihoods to accurately identify the true state of the system. We demonstrate the effectiveness of this approach to both identify the moment that a sensor becomes faulty and to correct for the resulting sensor behavior to maintain accurate estimates. We demonstrate our approach on an application of balloon navigation in the atmosphere and shuttle reentry. The results show that our method can accurately recover the true system state even in the presence of significant sensor bias, thereby improving the robustness and reliability of state estimation systems under challenging conditions. We also provide a statistical analysis of problem settings to determine when and where our method is most accurate and where it fails.
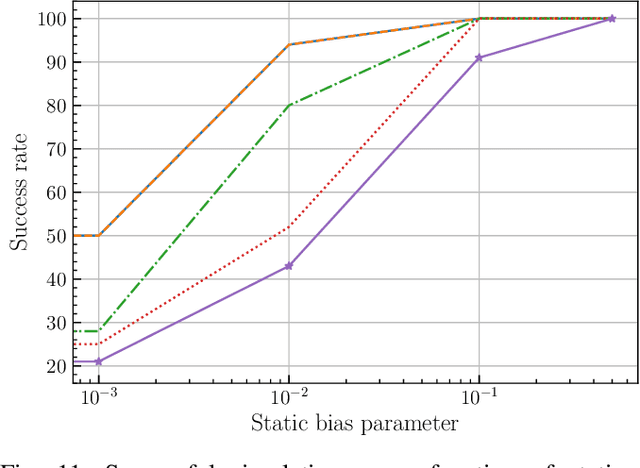
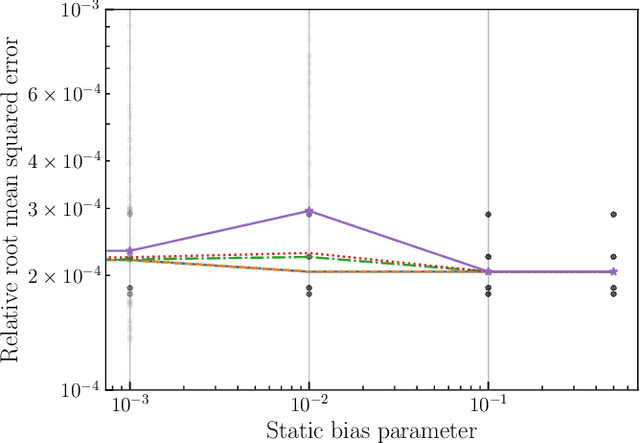
Improving the performance of Stein variational inference through extreme sparsification of physically-constrained neural network models
Jun 30, 2024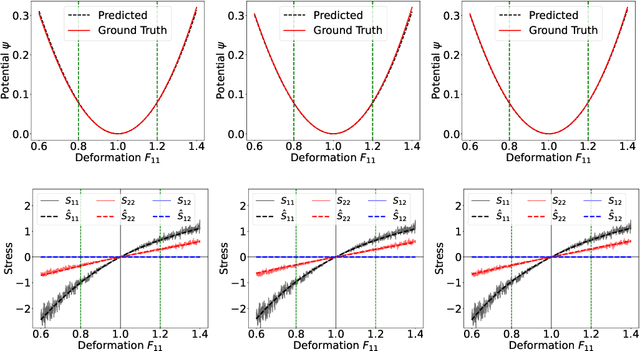
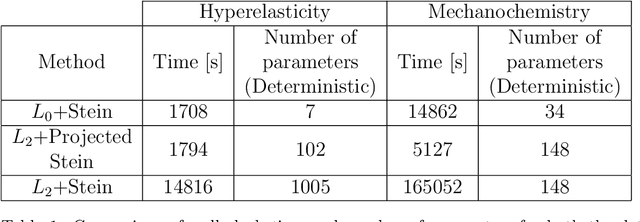
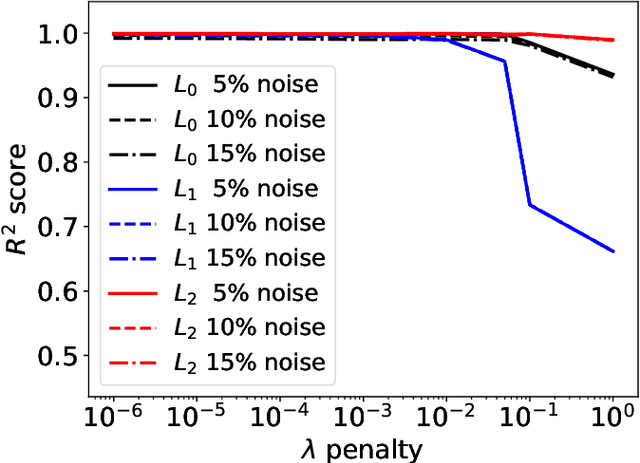
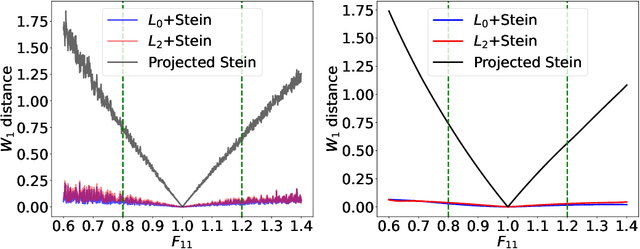
Abstract:Most scientific machine learning (SciML) applications of neural networks involve hundreds to thousands of parameters, and hence, uncertainty quantification for such models is plagued by the curse of dimensionality. Using physical applications, we show that $L_0$ sparsification prior to Stein variational gradient descent ($L_0$+SVGD) is a more robust and efficient means of uncertainty quantification, in terms of computational cost and performance than the direct application of SGVD or projected SGVD methods. Specifically, $L_0$+SVGD demonstrates superior resilience to noise, the ability to perform well in extrapolated regions, and a faster convergence rate to an optimal solution.
Bayesian calibration of stochastic agent based model via random forest
Jun 27, 2024Abstract:Agent-based models (ABM) provide an excellent framework for modeling outbreaks and interventions in epidemiology by explicitly accounting for diverse individual interactions and environments. However, these models are usually stochastic and highly parametrized, requiring precise calibration for predictive performance. When considering realistic numbers of agents and properly accounting for stochasticity, this high dimensional calibration can be computationally prohibitive. This paper presents a random forest based surrogate modeling technique to accelerate the evaluation of ABMs and demonstrates its use to calibrate an epidemiological ABM named CityCOVID via Markov chain Monte Carlo (MCMC). The technique is first outlined in the context of CityCOVID's quantities of interest, namely hospitalizations and deaths, by exploring dimensionality reduction via temporal decomposition with principal component analysis (PCA) and via sensitivity analysis. The calibration problem is then presented and samples are generated to best match COVID-19 hospitalization and death numbers in Chicago from March to June in 2020. These results are compared with previous approximate Bayesian calibration (IMABC) results and their predictive performance is analyzed showing improved performance with a reduction in computation.
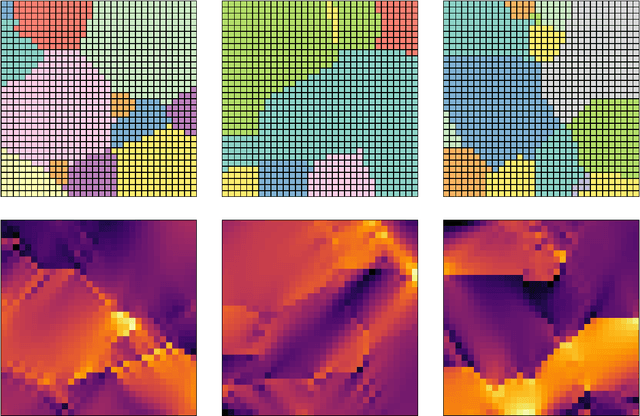
Accelerating Phase Field Simulations Through a Hybrid Adaptive Fourier Neural Operator with U-Net Backbone
Jun 24, 2024Abstract:Prolonged contact between a corrosive liquid and metal alloys can cause progressive dealloying. For such liquid-metal dealloying (LMD) process, phase field models have been developed. However, the governing equations often involve coupled non-linear partial differential equations (PDE), which are challenging to solve numerically. In particular, stiffness in the PDEs requires an extremely small time steps (e.g. $10^{-12}$ or smaller). This computational bottleneck is especially problematic when running LMD simulation until a late time horizon is required. This motivates the development of surrogate models capable of leaping forward in time, by skipping several consecutive time steps at-once. In this paper, we propose U-Shaped Adaptive Fourier Neural Operators (U-AFNO), a machine learning (ML) model inspired by recent advances in neural operator learning. U-AFNO employs U-Nets for extracting and reconstructing local features within the physical fields, and passes the latent space through a vision transformer (ViT) implemented in the Fourier space (AFNO). We use U-AFNOs to learn the dynamics mapping the field at a current time step into a later time step. We also identify global quantities of interest (QoI) describing the corrosion process (e.g. the deformation of the liquid-metal interface) and show that our proposed U-AFNO model is able to accurately predict the field dynamics, in-spite of the chaotic nature of LMD. Our model reproduces the key micro-structure statistics and QoIs with a level of accuracy on-par with the high-fidelity numerical solver. We also investigate the opportunity of using hybrid simulations, in which we alternate forward leap in time using the U-AFNO with high-fidelity time stepping. We demonstrate that while advantageous for some surrogate model design choices, our proposed U-AFNO model in fully auto-regressive settings consistently outperforms hybrid schemes.
Uncertainty Quantification of Graph Convolution Neural Network Models of Evolving Processes
Feb 17, 2024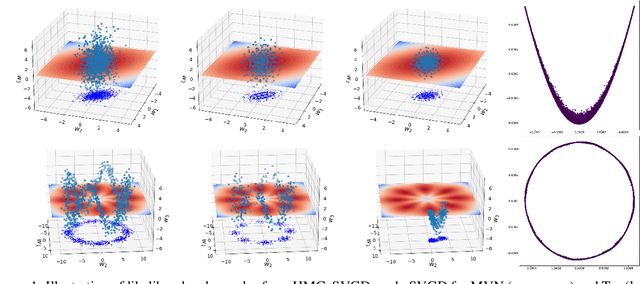
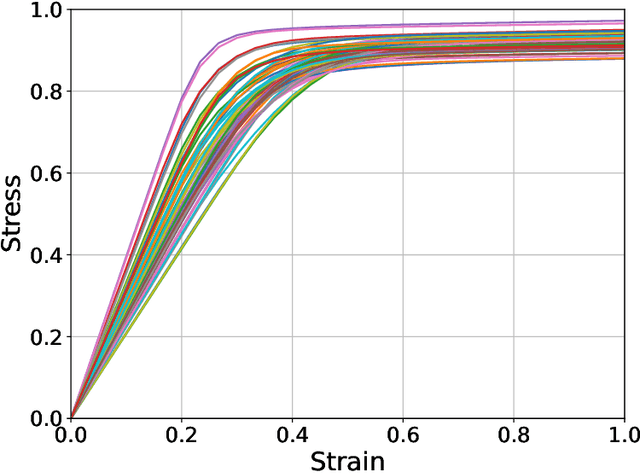
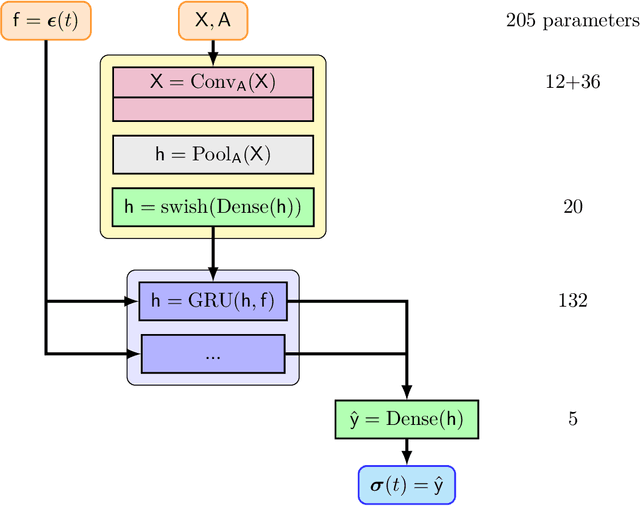
Abstract:The application of neural network models to scientific machine learning tasks has proliferated in recent years. In particular, neural network models have proved to be adept at modeling processes with spatial-temporal complexity. Nevertheless, these highly parameterized models have garnered skepticism in their ability to produce outputs with quantified error bounds over the regimes of interest. Hence there is a need to find uncertainty quantification methods that are suitable for neural networks. In this work we present comparisons of the parametric uncertainty quantification of neural networks modeling complex spatial-temporal processes with Hamiltonian Monte Carlo and Stein variational gradient descent and its projected variant. Specifically we apply these methods to graph convolutional neural network models of evolving systems modeled with recurrent neural network and neural ordinary differential equations architectures. We show that Stein variational inference is a viable alternative to Monte Carlo methods with some clear advantages for complex neural network models. For our exemplars, Stein variational interference gave similar uncertainty profiles through time compared to Hamiltonian Monte Carlo, albeit with generally more generous variance.Projected Stein variational gradient descent also produced similar uncertainty profiles to the non-projected counterpart, but large reductions in the active weight space were confounded by the stability of the neural network predictions and the convoluted likelihood landscape.
Enhancing Polynomial Chaos Expansion Based Surrogate Modeling using a Novel Probabilistic Transfer Learning Strategy
Dec 07, 2023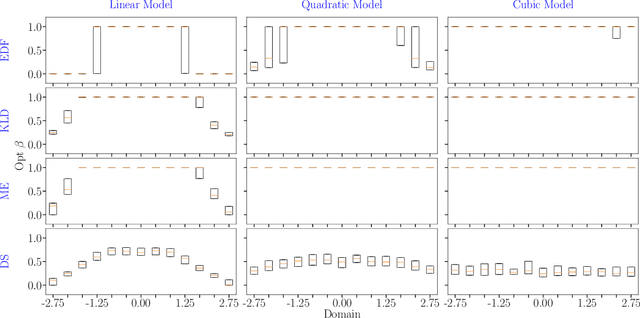
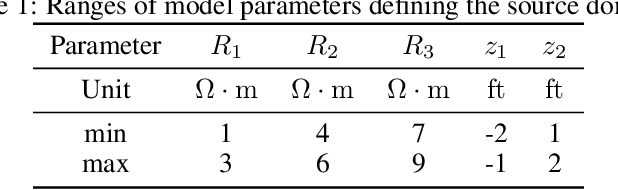
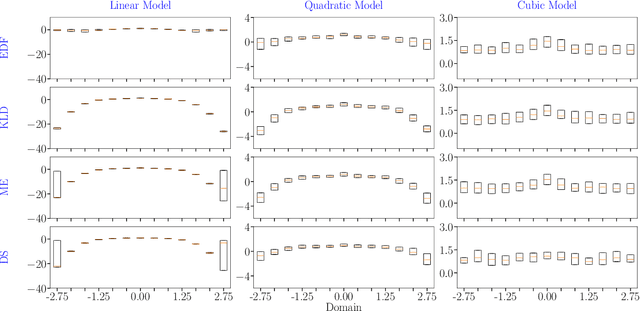
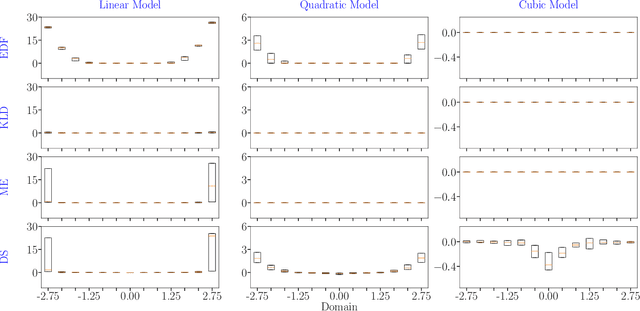
Abstract:In the field of surrogate modeling, polynomial chaos expansion (PCE) allows practitioners to construct inexpensive yet accurate surrogates to be used in place of the expensive forward model simulations. For black-box simulations, non-intrusive PCE allows the construction of these surrogates using a set of simulation response evaluations. In this context, the PCE coefficients can be obtained using linear regression, which is also known as point collocation or stochastic response surfaces. Regression exhibits better scalability and can handle noisy function evaluations in contrast to other non-intrusive approaches, such as projection. However, since over-sampling is generally advisable for the linear regression approach, the simulation requirements become prohibitive for expensive forward models. We propose to leverage transfer learning whereby knowledge gained through similar PCE surrogate construction tasks (source domains) is transferred to a new surrogate-construction task (target domain) which has a limited number of forward model simulations (training data). The proposed transfer learning strategy determines how much, if any, information to transfer using new techniques inspired by Bayesian modeling and data assimilation. The strategy is scrutinized using numerical investigations and applied to an engineering problem from the oil and gas industry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge