Condensed Stein Variational Gradient Descent for Uncertainty Quantification of Neural Networks
Paper and Code
Dec 21, 2024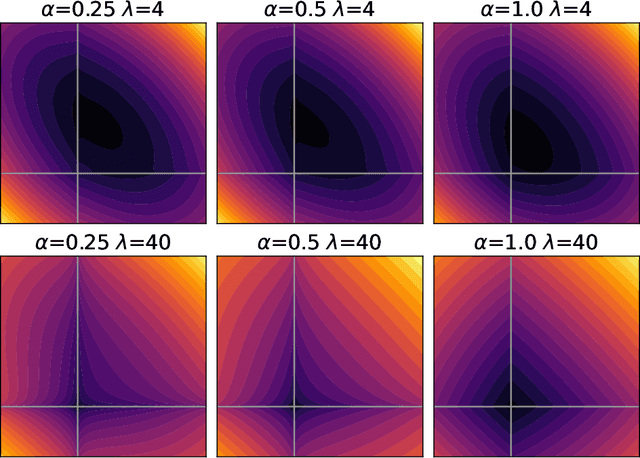
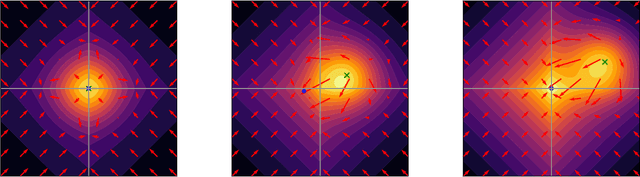
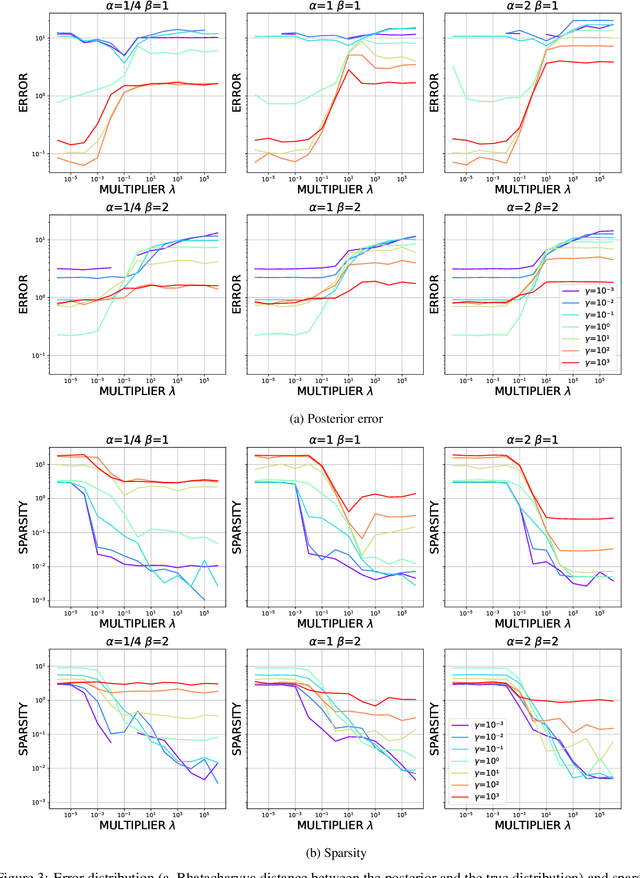
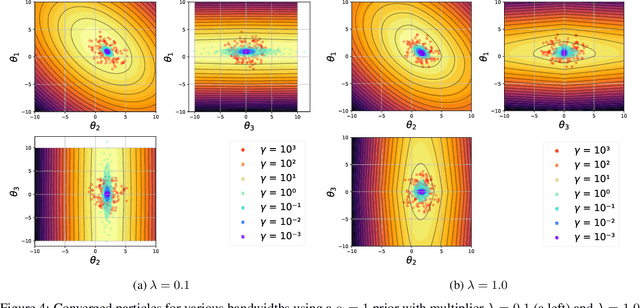
We propose a Stein variational gradient descent method to concurrently sparsify, train, and provide uncertainty quantification of a complexly parameterized model such as a neural network. It employs a graph reconciliation and condensation process to reduce complexity and increase similarity in the Stein ensemble of parameterizations. Therefore, the proposed condensed Stein variational gradient (cSVGD) method provides uncertainty quantification on parameters, not just outputs. Furthermore, the parameter reduction speeds up the convergence of the Stein gradient descent as it reduces the combinatorial complexity by aligning and differentiating the sensitivity to parameters. These properties are demonstrated with an illustrative example and an application to a representation problem in solid mechanics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge