Condensed Stein Variational Gradient Descent for Uncertainty Quantification of Neural Networks

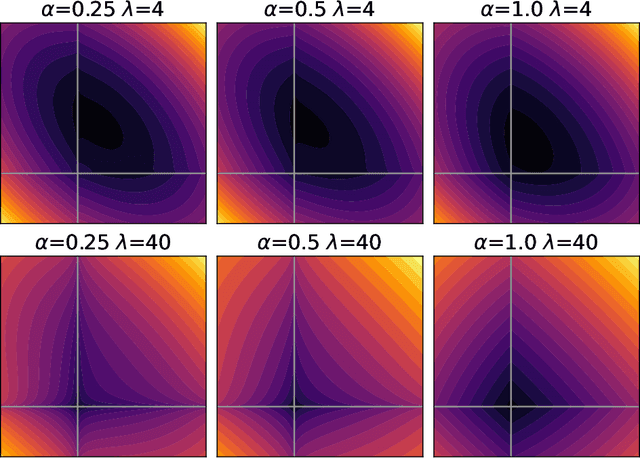
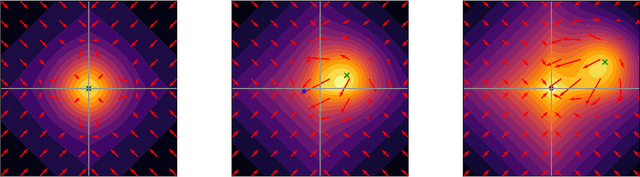
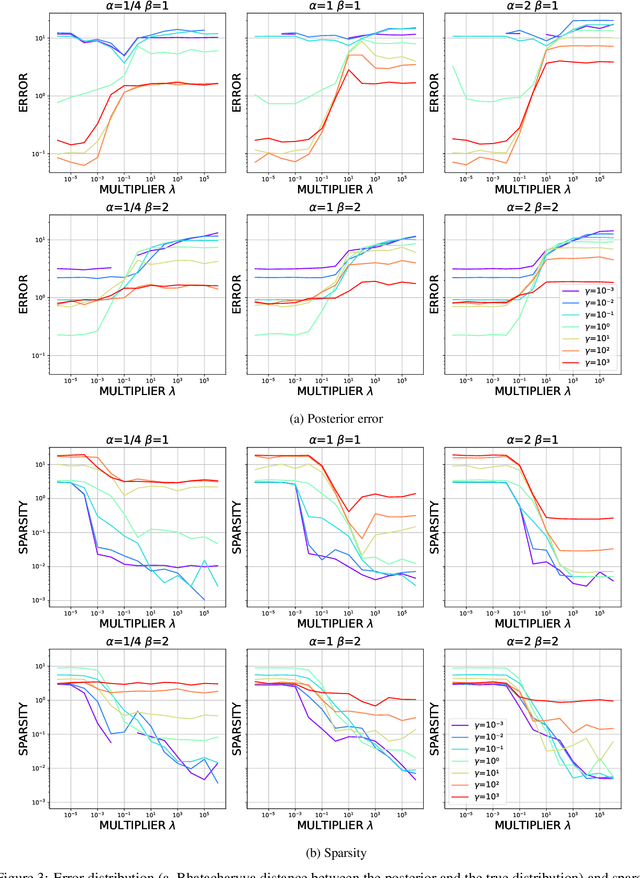
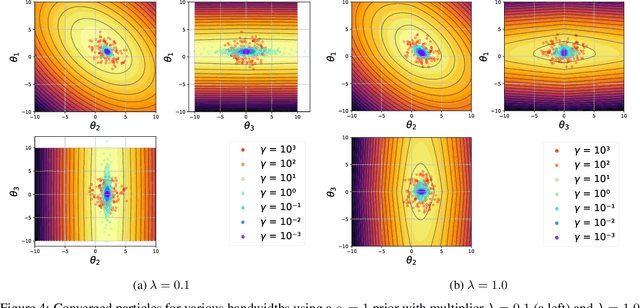
We propose a Stein variational gradient descent method to concurrently sparsify, train, and provide uncertainty quantification of a complexly parameterized model such as a neural network. It employs a graph reconciliation and condensation process to reduce complexity and increase similarity in the Stein ensemble of parameterizations. Therefore, the proposed condensed Stein variational gradient (cSVGD) method provides uncertainty quantification on parameters, not just outputs. Furthermore, the parameter reduction speeds up the convergence of the Stein gradient descent as it reduces the combinatorial complexity by aligning and differentiating the sensitivity to parameters. These properties are demonstrated with an illustrative example and an application to a representation problem in solid mechanics.

Improving the performance of Stein variational inference through extreme sparsification of physically-constrained neural network models

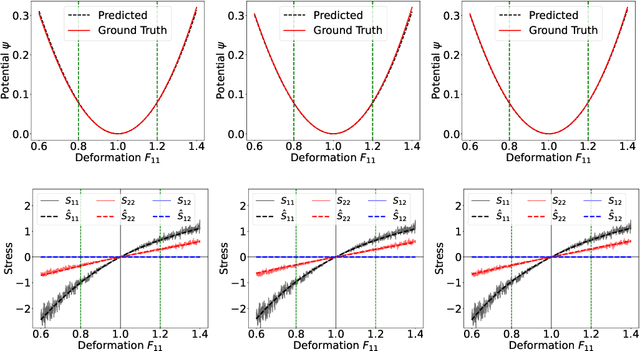
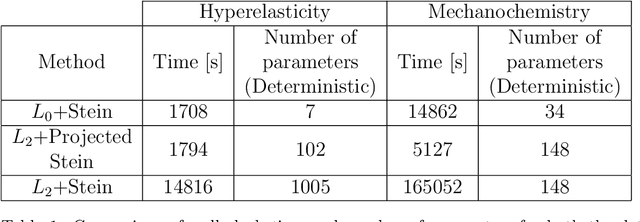
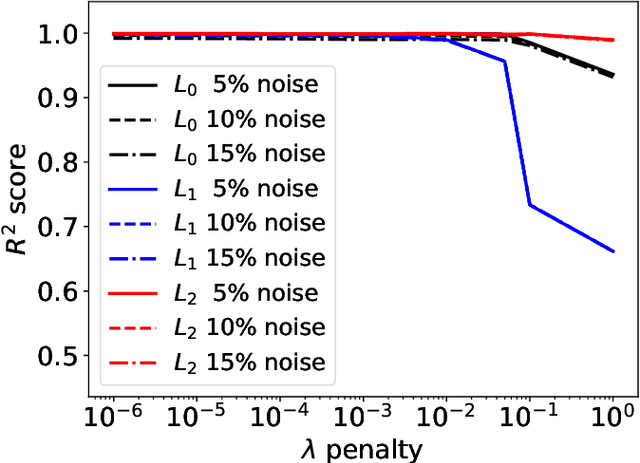
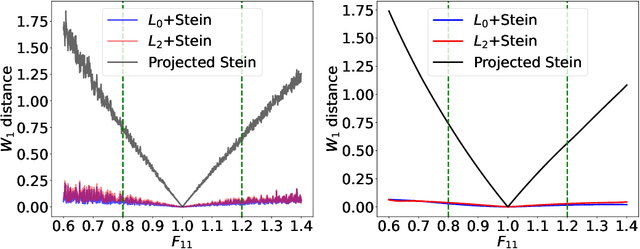
Most scientific machine learning (SciML) applications of neural networks involve hundreds to thousands of parameters, and hence, uncertainty quantification for such models is plagued by the curse of dimensionality. Using physical applications, we show that $L_0$ sparsification prior to Stein variational gradient descent ($L_0$+SVGD) is a more robust and efficient means of uncertainty quantification, in terms of computational cost and performance than the direct application of SGVD or projected SGVD methods. Specifically, $L_0$+SVGD demonstrates superior resilience to noise, the ability to perform well in extrapolated regions, and a faster convergence rate to an optimal solution.

A review on data-driven constitutive laws for solids

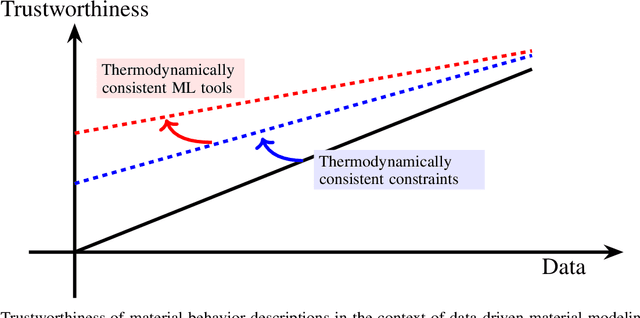
This review article highlights state-of-the-art data-driven techniques to discover, encode, surrogate, or emulate constitutive laws that describe the path-independent and path-dependent response of solids. Our objective is to provide an organized taxonomy to a large spectrum of methodologies developed in the past decades and to discuss the benefits and drawbacks of the various techniques for interpreting and forecasting mechanics behavior across different scales. Distinguishing between machine-learning-based and model-free methods, we further categorize approaches based on their interpretability and on their learning process/type of required data, while discussing the key problems of generalization and trustworthiness. We attempt to provide a road map of how these can be reconciled in a data-availability-aware context. We also touch upon relevant aspects such as data sampling techniques, design of experiments, verification, and validation.

Extreme sparsification of physics-augmented neural networks for interpretable model discovery in mechanics

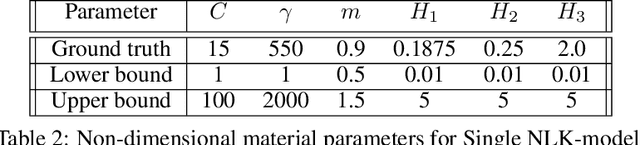
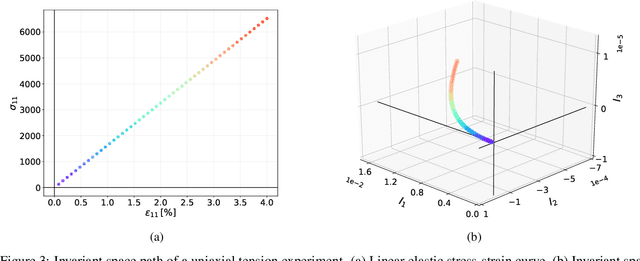
Data-driven constitutive modeling with neural networks has received increased interest in recent years due to its ability to easily incorporate physical and mechanistic constraints and to overcome the challenging and time-consuming task of formulating phenomenological constitutive laws that can accurately capture the observed material response. However, even though neural network-based constitutive laws have been shown to generalize proficiently, the generated representations are not easily interpretable due to their high number of trainable parameters. Sparse regression approaches exist that allow to obtaining interpretable expressions, but the user is tasked with creating a library of model forms which by construction limits their expressiveness to the functional forms provided in the libraries. In this work, we propose to train regularized physics-augmented neural network-based constitutive models utilizing a smoothed version of $L^{0}$-regularization. This aims to maintain the trustworthiness inherited by the physical constraints, but also enables interpretability which has not been possible thus far on any type of machine learning-based constitutive model where model forms were not assumed a-priory but were actually discovered. During the training process, the network simultaneously fits the training data and penalizes the number of active parameters, while also ensuring constitutive constraints such as thermodynamic consistency. We show that the method can reliably obtain interpretable and trustworthy constitutive models for compressible and incompressible hyperelasticity, yield functions, and hardening models for elastoplasticity, for synthetic and experimental data.

Stress representations for tensor basis neural networks: alternative formulations to Finger-Rivlin-Ericksen

Data-driven constitutive modeling frameworks based on neural networks and classical representation theorems have recently gained considerable attention due to their ability to easily incorporate constitutive constraints and their excellent generalization performance. In these models, the stress prediction follows from a linear combination of invariant-dependent coefficient functions and known tensor basis generators. However, thus far the formulations have been limited to stress representations based on the classical Rivlin and Ericksen form, while the performance of alternative representations has yet to be investigated. In this work, we survey a variety of tensor basis neural network models for modeling hyperelastic materials in a finite deformation context, including a number of so far unexplored formulations which use theoretically equivalent invariants and generators to Finger-Rivlin-Ericksen. Furthermore, we compare potential-based and coefficient-based approaches, as well as different calibration techniques. Nine variants are tested against both noisy and noiseless datasets for three different materials. Theoretical and practical insights into the performance of each formulation are given.

Modular machine learning-based elastoplasticity: generalization in the context of limited data

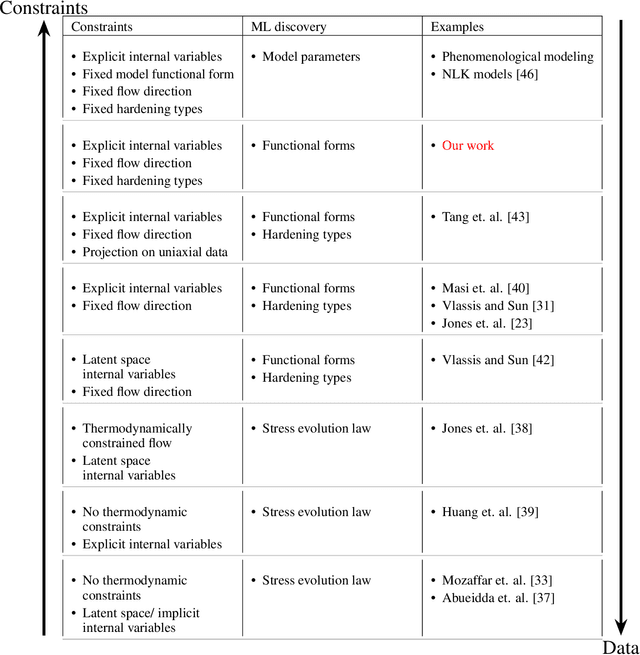
The development of accurate constitutive models for materials that undergo path-dependent processes continues to be a complex challenge in computational solid mechanics. Challenges arise both in considering the appropriate model assumptions and from the viewpoint of data availability, verification, and validation. Recently, data-driven modeling approaches have been proposed that aim to establish stress-evolution laws that avoid user-chosen functional forms by relying on machine learning representations and algorithms. However, these approaches not only require a significant amount of data but also need data that probes the full stress space with a variety of complex loading paths. Furthermore, they rarely enforce all necessary thermodynamic principles as hard constraints. Hence, they are in particular not suitable for low-data or limited-data regimes, where the first arises from the cost of obtaining the data and the latter from the experimental limitations of obtaining labeled data, which is commonly the case in engineering applications. In this work, we discuss a hybrid framework that can work on a variable amount of data by relying on the modularity of the elastoplasticity formulation where each component of the model can be chosen to be either a classical phenomenological or a data-driven model depending on the amount of available information and the complexity of the response. The method is tested on synthetic uniaxial data coming from simulations as well as cyclic experimental data for structural materials. The discovered material models are found to not only interpolate well but also allow for accurate extrapolation in a thermodynamically consistent manner far outside the domain of the training data. Training aspects and details of the implementation of these models into Finite Element simulations are discussed and analyzed.

Reduced order modeling with Barlow Twins self-supervised learning: Navigating the space between linear and nonlinear solution manifolds

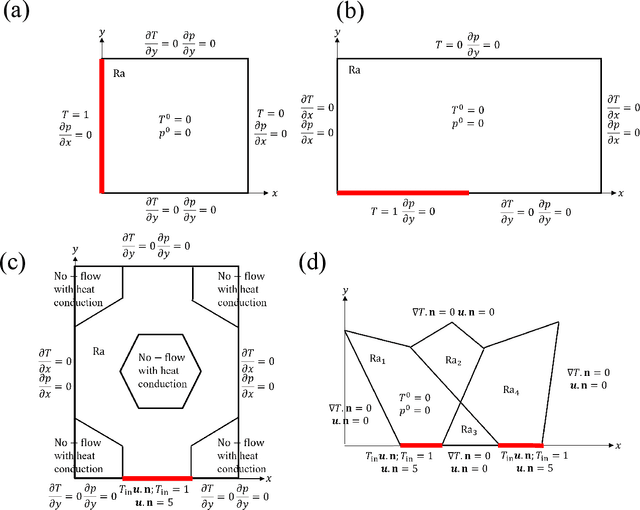
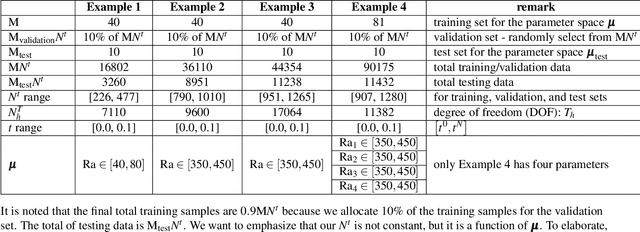
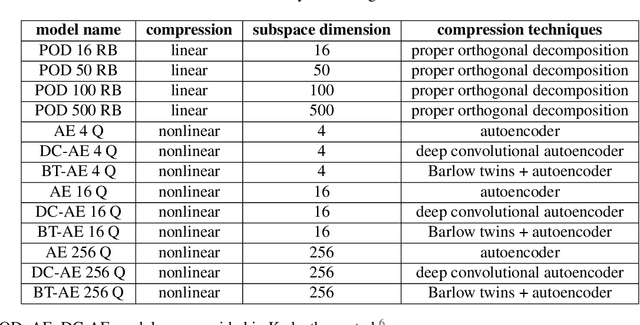
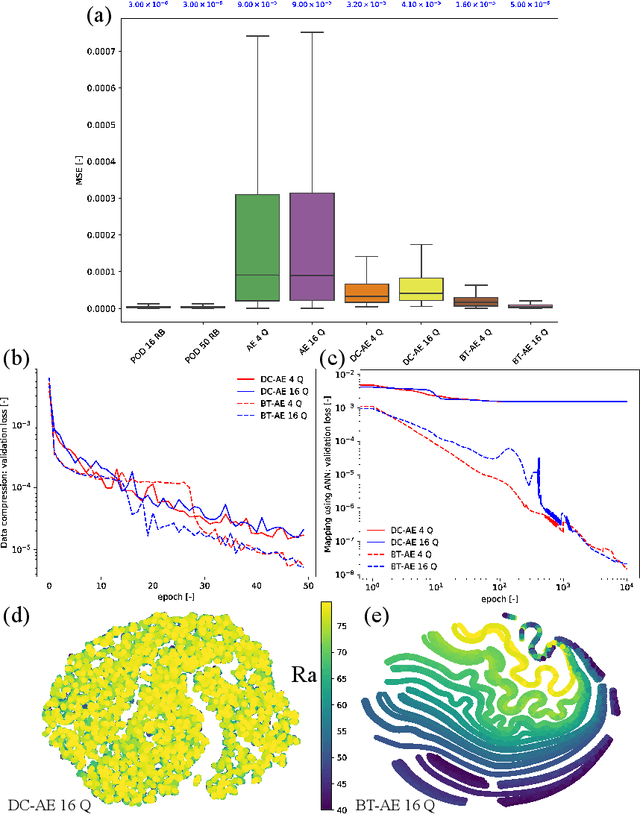
We propose a unified data-driven reduced order model (ROM) that bridges the performance gap between linear and nonlinear manifold approaches. Deep learning ROM (DL-ROM) using deep-convolutional autoencoders (DC-AE) has been shown to capture nonlinear solution manifolds but fails to perform adequately when linear subspace approaches such as proper orthogonal decomposition (POD) would be optimal. Besides, most DL-ROM models rely on convolutional layers, which might limit its application to only a structured mesh. The proposed framework in this study relies on the combination of an autoencoder (AE) and Barlow Twins (BT) self-supervised learning, where BT maximizes the information content of the embedding with the latent space through a joint embedding architecture. Through a series of benchmark problems of natural convection in porous media, BT-AE performs better than the previous DL-ROM framework by providing comparable results to POD-based approaches for problems where the solution lies within a linear subspace as well as DL-ROM autoencoder-based techniques where the solution lies on a nonlinear manifold; consequently, bridges the gap between linear and nonlinear reduced manifolds. Furthermore, this BT-AE framework can operate on unstructured meshes, which provides flexibility in its application to standard numerical solvers, on-site measurements, experimental data, or a combination of these sources.

Interval and fuzzy physics-informed neural networks for uncertain fields

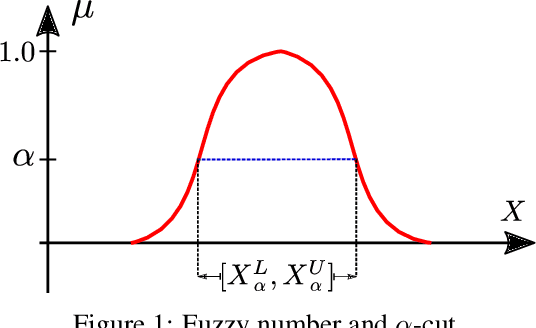
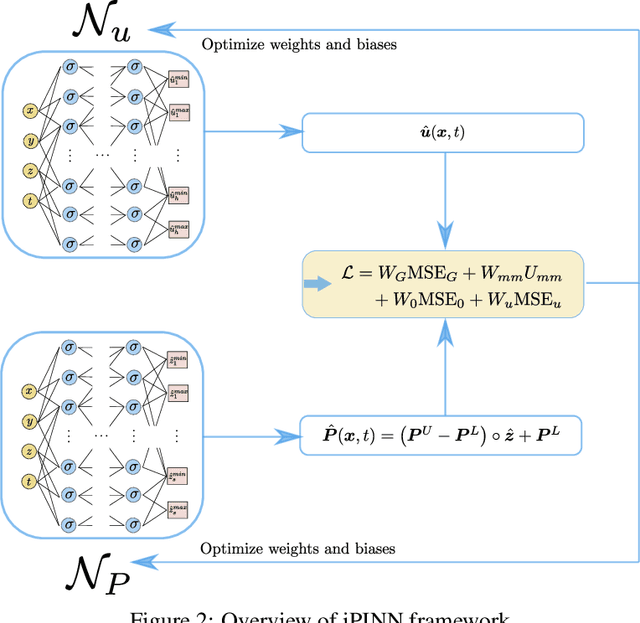
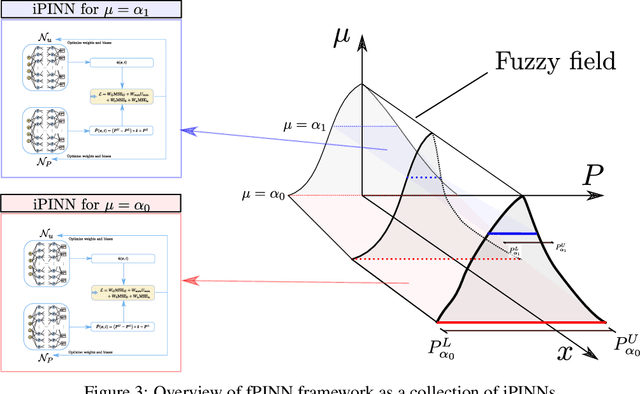
Temporally and spatially dependent uncertain parameters are regularly encountered in engineering applications. Commonly these uncertainties are accounted for using random fields and processes which require knowledge about the appearing probability distributions functions which is not readily available. In these cases non-probabilistic approaches such as interval analysis and fuzzy set theory are helpful uncertainty measures. Partial differential equations involving fuzzy and interval fields are traditionally solved using the finite element method where the input fields are sampled using some basis function expansion methods. This approach however is problematic, as it is reliant on knowledge about the spatial correlation fields. In this work we utilize physics-informed neural networks (PINNs) to solve interval and fuzzy partial differential equations. The resulting network structures termed interval physics-informed neural networks (iPINNs) and fuzzy physics-informed neural networks (fPINNs) show promising results for obtaining bounded solutions of equations involving spatially uncertain parameter fields. In contrast to finite element approaches, no correlation length specification of the input fields as well as no averaging via Monte-Carlo simulations are necessary. In fact, information about the input interval fields is obtained directly as a byproduct of the presented solution scheme. Furthermore, all major advantages of PINNs are retained, i.e. meshfree nature of the scheme, and ease of inverse problem set-up.

A framework for data-driven solution and parameter estimation of PDEs using conditional generative adversarial networks

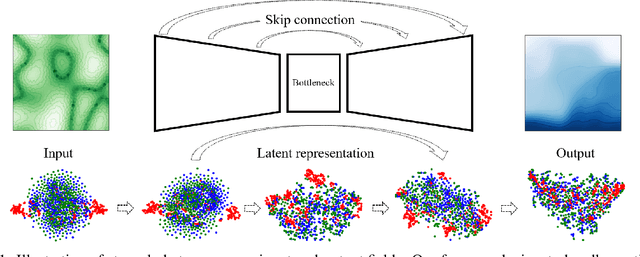
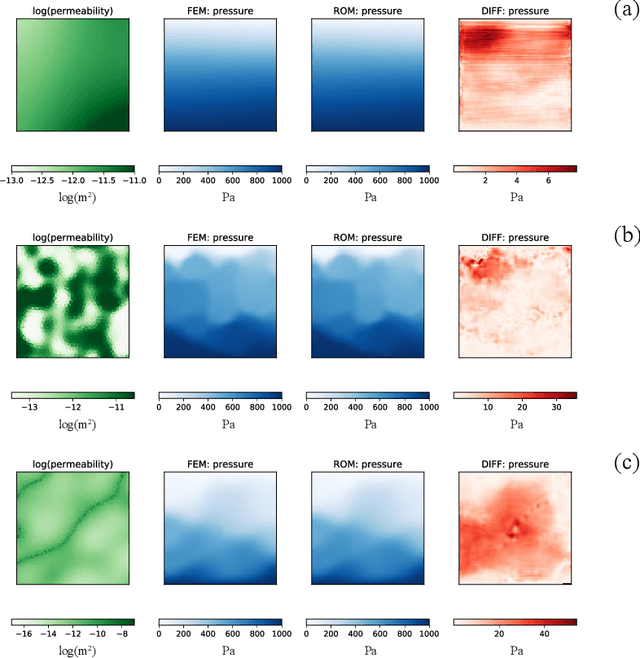
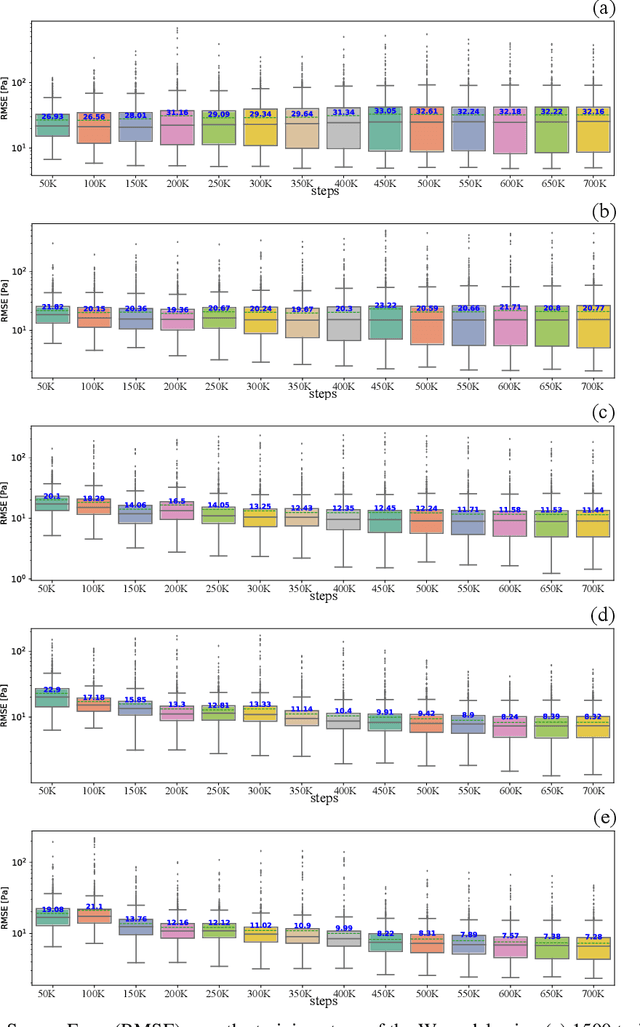
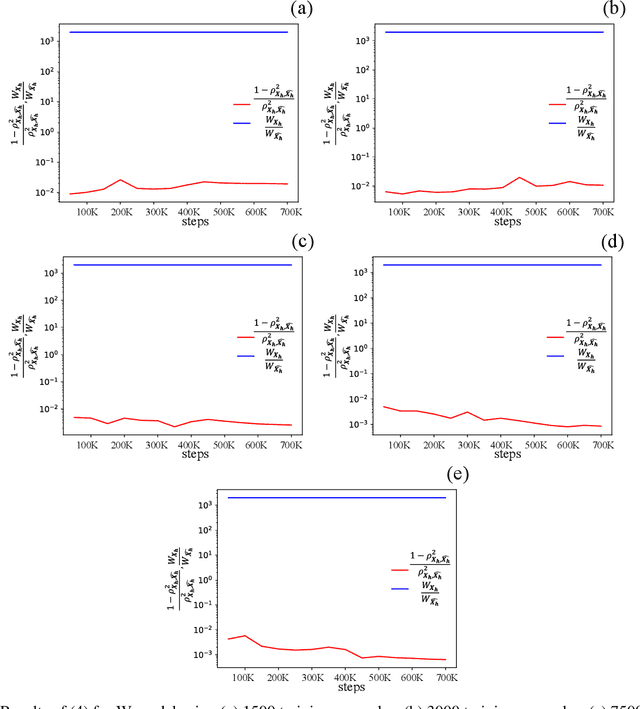
This work is the first to employ and adapt the image-to-image translation concept based on conditional generative adversarial networks (cGAN) towards learning a forward and an inverse solution operator of partial differential equations (PDEs). Even though the proposed framework could be applied as a surrogate model for the solution of any PDEs, here we focus on steady-state solutions of coupled hydro-mechanical processes in heterogeneous porous media. Strongly heterogeneous material properties, which translate to the heterogeneity of coefficients of the PDEs and discontinuous features in the solutions, require specialized techniques for the forward and inverse solution of these problems. Additionally, parametrization of the spatially heterogeneous coefficients is excessively difficult by using standard reduced order modeling techniques. In this work, we overcome these challenges by employing the image-to-image translation concept to learn the forward and inverse solution operators and utilize a U-Net generator and a patch-based discriminator. Our results show that the proposed data-driven reduced order model has competitive predictive performance capabilities in accuracy and computational efficiency as well as training time requirements compared to state-of-the-art data-driven methods for both forward and inverse problems.

Local approximate Gaussian process regression for data-driven constitutive laws: Development and comparison with neural networks

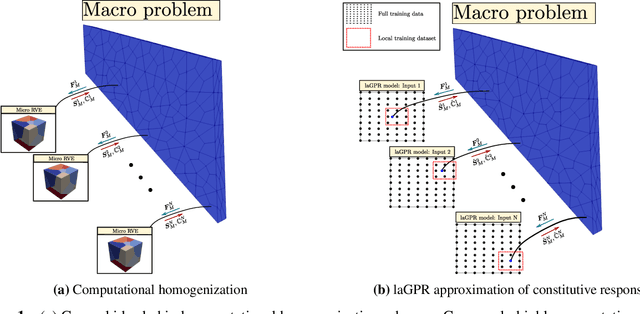
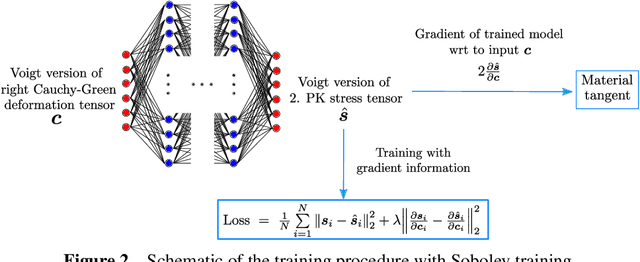
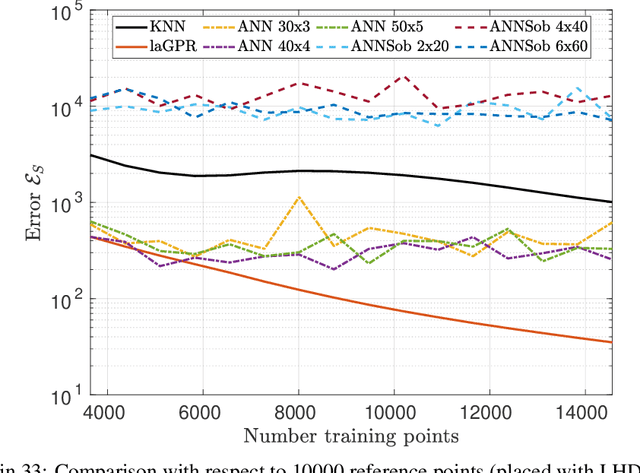
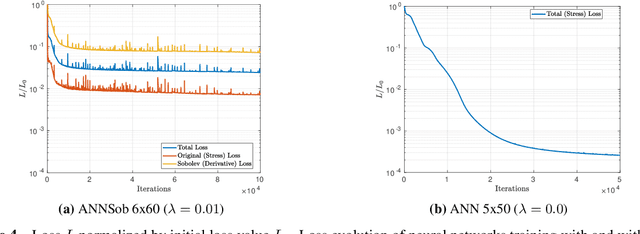
Hierarchical computational methods for multiscale mechanics such as the FE$^2$ and FE-FFT methods are generally accompanied by high computational costs. Data-driven approaches are able to speed the process up significantly by enabling to incorporate the effective micromechanical response in macroscale simulations without the need of performing additional computations at each Gauss point explicitly. Traditionally artificial neural networks (ANNs) have been the surrogate modeling technique of choice in the solid mechanics community. However they suffer from severe drawbacks due to their parametric nature and suboptimal training and inference properties for the investigated datasets in a three dimensional setting. These problems can be avoided using local approximate Gaussian process regression (laGPR). This method can allow the prediction of stress outputs at particular strain space locations by training local regression models based on Gaussian processes, using only a subset of the data for each local model, offering better and more reliable accuracy than ANNs. A modified Newton-Raphson approach is proposed to accommodate for the local nature of the laGPR approximation when solving the global structural problem in a FE setting. Hence, the presented work offers a complete and general framework enabling multiscale calculations combining a data-driven constitutive prediction using laGPR, and macroscopic calculations using an FE scheme that we test for finite-strain three-dimensional hyperelastic problems.