Reduced Order Modeling of Energetic Materials Using Physics-Aware Recurrent Convolutional Neural Networks in a Latent Space (LatentPARC)

Physics-aware deep learning (PADL) has gained popularity for use in complex spatiotemporal dynamics (field evolution) simulations, such as those that arise frequently in computational modeling of energetic materials (EM). Here, we show that the challenge PADL methods face while learning complex field evolution problems can be simplified and accelerated by decoupling it into two tasks: learning complex geometric features in evolving fields and modeling dynamics over these features in a lower dimensional feature space. To accomplish this, we build upon our previous work on physics-aware recurrent convolutions (PARC). PARC embeds knowledge of underlying physics into its neural network architecture for more robust and accurate prediction of evolving physical fields. PARC was shown to effectively learn complex nonlinear features such as the formation of hotspots and coupled shock fronts in various initiation scenarios of EMs, as a function of microstructures, serving effectively as a microstructure-aware burn model. In this work, we further accelerate PARC and reduce its computational cost by projecting the original dynamics onto a lower-dimensional invariant manifold, or 'latent space.' The projected latent representation encodes the complex geometry of evolving fields (e.g. temperature and pressure) in a set of data-driven features. The reduced dimension of this latent space allows us to learn the dynamics during the initiation of EM with a lighter and more efficient model. We observe a significant decrease in training and inference time while maintaining results comparable to PARC at inference. This work takes steps towards enabling rapid prediction of EM thermomechanics at larger scales and characterization of EM structure-property-performance linkages at a full application scale.

Rollout-LaSDI: Enhancing the long-term accuracy of Latent Space Dynamics

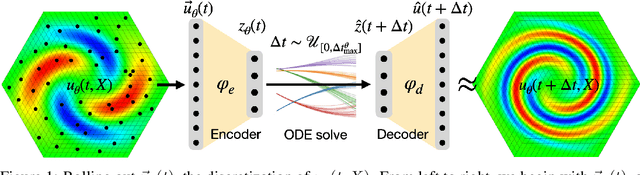
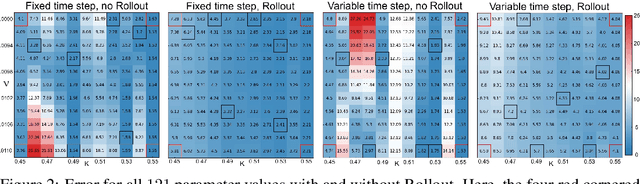
Solving complex partial differential equations is vital in the physical sciences, but often requires computationally expensive numerical methods. Reduced-order models (ROMs) address this by exploiting dimensionality reduction to create fast approximations. While modern ROMs can solve parameterized families of PDEs, their predictive power degrades over long time horizons. We address this by (1) introducing a flexible, high-order, yet inexpensive finite-difference scheme and (2) proposing a Rollout loss that trains ROMs to make accurate predictions over arbitrary time horizons. We demonstrate our approach on the 2D Burgers equation.

mLaSDI: Multi-stage latent space dynamics identification

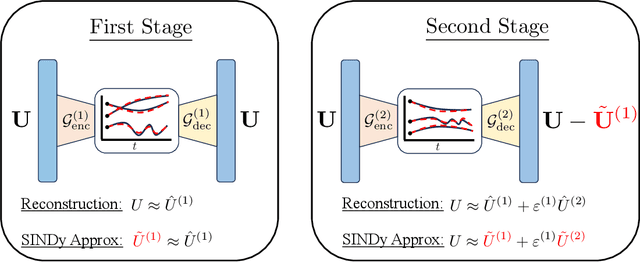
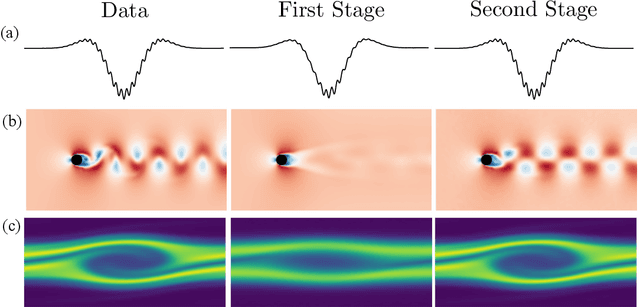
Determining accurate numerical solutions of partial differential equations (PDEs) is an important task in many scientific disciplines. However, solvers can be computationally expensive, leading to the development of reduced-order models (ROMs). Recently, Latent Space Dynamics Identification (LaSDI) was proposed as a data-driven, non-intrusive ROM framework. LaSDI compresses the training data using an autoencoder and learns a system of user-chosen ordinary differential equations (ODEs), which govern the latent space dynamics. This allows for rapid predictions by interpolating and evolving the low-dimensional ODEs in the latent space. While LaSDI has produced effective ROMs for numerous problems, the autoencoder can have difficulty accurately reconstructing training data while also satisfying the imposed dynamics in the latent space, particularly in complex or high-frequency regimes. To address this, we propose multi-stage Latent Space Dynamics Identification (mLaSDI). With mLaSDI, several autoencoders are trained sequentially in stages, where each autoencoder learns to correct the error of the previous stages. We find that applying mLaSDI with small autoencoders results in lower prediction and reconstruction errors, while also reducing training time compared to LaSDI.

Thermodynamically Consistent Latent Dynamics Identification for Parametric Systems

We propose an efficient thermodynamics-informed latent space dynamics identification (tLaSDI) framework for the reduced-order modeling of parametric nonlinear dynamical systems. This framework integrates autoencoders for dimensionality reduction with newly developed parametric GENERIC formalism-informed neural networks (pGFINNs), which enable efficient learning of parametric latent dynamics while preserving key thermodynamic principles such as free energy conservation and entropy generation across the parameter space. To further enhance model performance, a physics-informed active learning strategy is incorporated, leveraging a greedy, residual-based error indicator to adaptively sample informative training data, outperforming uniform sampling at equivalent computational cost. Numerical experiments on the Burgers' equation and the 1D/1V Vlasov-Poisson equation demonstrate that the proposed method achieves up to 3,528x speed-up with 1-3% relative errors, and significant reduction in training (50-90%) and inference (57-61%) cost. Moreover, the learned latent space dynamics reveal the underlying thermodynamic behavior of the system, offering valuable insights into the physical-space dynamics.

Defining Foundation Models for Computational Science: A Call for Clarity and Rigor

The widespread success of foundation models in natural language processing and computer vision has inspired researchers to extend the concept to scientific machine learning and computational science. However, this position paper argues that as the term "foundation model" is an evolving concept, its application in computational science is increasingly used without a universally accepted definition, potentially creating confusion and diluting its precise scientific meaning. In this paper, we address this gap by proposing a formal definition of foundation models in computational science, grounded in the core values of generality, reusability, and scalability. We articulate a set of essential and desirable characteristics that such models must exhibit, drawing parallels with traditional foundational methods, like the finite element and finite volume methods. Furthermore, we introduce the Data-Driven Finite Element Method (DD-FEM), a framework that fuses the modular structure of classical FEM with the representational power of data-driven learning. We demonstrate how DD-FEM addresses many of the key challenges in realizing foundation models for computational science, including scalability, adaptability, and physics consistency. By bridging traditional numerical methods with modern AI paradigms, this work provides a rigorous foundation for evaluating and developing novel approaches toward future foundation models in computational science.

Physics-informed reduced order model with conditional neural fields

This study presents the conditional neural fields for reduced-order modeling (CNF-ROM) framework to approximate solutions of parametrized partial differential equations (PDEs). The approach combines a parametric neural ODE (PNODE) for modeling latent dynamics over time with a decoder that reconstructs PDE solutions from the corresponding latent states. We introduce a physics-informed learning objective for CNF-ROM, which includes two key components. First, the framework uses coordinate-based neural networks to calculate and minimize PDE residuals by computing spatial derivatives via automatic differentiation and applying the chain rule for time derivatives. Second, exact initial and boundary conditions (IC/BC) are imposed using approximate distance functions (ADFs) [Sukumar and Srivastava, CMAME, 2022]. However, ADFs introduce a trade-off as their second- or higher-order derivatives become unstable at the joining points of boundaries. To address this, we introduce an auxiliary network inspired by [Gladstone et al., NeurIPS ML4PS workshop, 2022]. Our method is validated through parameter extrapolation and interpolation, temporal extrapolation, and comparisons with analytical solutions.

Data-Driven, Parameterized Reduced-order Models for Predicting Distortion in Metal 3D Printing

In Laser Powder Bed Fusion (LPBF), the applied laser energy produces high thermal gradients that lead to unacceptable final part distortion. Accurate distortion prediction is essential for optimizing the 3D printing process and manufacturing a part that meets geometric accuracy requirements. This study introduces data-driven parameterized reduced-order models (ROMs) to predict distortion in LPBF across various machine process settings. We propose a ROM framework that combines Proper Orthogonal Decomposition (POD) with Gaussian Process Regression (GPR) and compare its performance against a deep-learning based parameterized graph convolutional autoencoder (GCA). The POD-GPR model demonstrates high accuracy, predicting distortions within $\pm0.001mm$, and delivers a computational speed-up of approximately 1800x.

Quantifying Qualitative Insights: Leveraging LLMs to Market Predict

Recent advancements in Large Language Models (LLMs) have the potential to transform financial analytics by integrating numerical and textual data. However, challenges such as insufficient context when fusing multimodal information and the difficulty in measuring the utility of qualitative outputs, which LLMs generate as text, have limited their effectiveness in tasks such as financial forecasting. This study addresses these challenges by leveraging daily reports from securities firms to create high-quality contextual information. The reports are segmented into text-based key factors and combined with numerical data, such as price information, to form context sets. By dynamically updating few-shot examples based on the query time, the sets incorporate the latest information, forming a highly relevant set closely aligned with the query point. Additionally, a crafted prompt is designed to assign scores to the key factors, converting qualitative insights into quantitative results. The derived scores undergo a scaling process, transforming them into real-world values that are used for prediction. Our experiments demonstrate that LLMs outperform time-series models in market forecasting, though challenges such as imperfect reproducibility and limited explainability remain.

WgLaSDI: Weak-Form Greedy Latent Space Dynamics Identification

The parametric greedy latent space dynamics identification (gLaSDI) framework has demonstrated promising potential for accurate and efficient modeling of high-dimensional nonlinear physical systems. However, it remains challenging to handle noisy data. To enhance robustness against noise, we incorporate the weak-form estimation of nonlinear dynamics (WENDy) into gLaSDI. In the proposed weak-form gLaSDI (WgLaSDI) framework, an autoencoder and WENDy are trained simultaneously to discover intrinsic nonlinear latent-space dynamics of high-dimensional data. Compared to the standard sparse identification of nonlinear dynamics (SINDy) employed in gLaSDI, WENDy enables variance reduction and robust latent space discovery, therefore leading to more accurate and efficient reduced-order modeling. Furthermore, the greedy physics-informed active learning in WgLaSDI enables adaptive sampling of optimal training data on the fly for enhanced modeling accuracy. The effectiveness of the proposed framework is demonstrated by modeling various nonlinear dynamical problems, including viscous and inviscid Burgers' equations, time-dependent radial advection, and the Vlasov equation for plasma physics. With data that contains 5-10% Gaussian white noise, WgLaSDI outperforms gLaSDI by orders of magnitude, achieving 1-7% relative errors. Compared with the high-fidelity models, WgLaSDI achieves 121 to 1,779x speed-up.

A Comprehensive Review of Latent Space Dynamics Identification Algorithms for Intrusive and Non-Intrusive Reduced-Order-Modeling

Numerical solvers of partial differential equations (PDEs) have been widely employed for simulating physical systems. However, the computational cost remains a major bottleneck in various scientific and engineering applications, which has motivated the development of reduced-order models (ROMs). Recently, machine-learning-based ROMs have gained significant popularity and are promising for addressing some limitations of traditional ROM methods, especially for advection dominated systems. In this chapter, we focus on a particular framework known as Latent Space Dynamics Identification (LaSDI), which transforms the high-fidelity data, governed by a PDE, to simpler and low-dimensional latent-space data, governed by ordinary differential equations (ODEs). These ODEs can be learned and subsequently interpolated to make ROM predictions. Each building block of LaSDI can be easily modulated depending on the application, which makes the LaSDI framework highly flexible. In particular, we present strategies to enforce the laws of thermodynamics into LaSDI models (tLaSDI), enhance robustness in the presence of noise through the weak form (WLaSDI), select high-fidelity training data efficiently through active learning (gLaSDI, GPLaSDI), and quantify the ROM prediction uncertainty through Gaussian processes (GPLaSDI). We demonstrate the performance of different LaSDI approaches on Burgers equation, a non-linear heat conduction problem, and a plasma physics problem, showing that LaSDI algorithms can achieve relative errors of less than a few percent and up to thousands of times speed-ups.