WGFINNs: Weak formulation-based GENERIC formalism informed neural networks'

Data-driven discovery of governing equations from noisy observations remains a fundamental challenge in scientific machine learning. While GENERIC formalism informed neural networks (GFINNs) provide a principled framework that enforces the laws of thermodynamics by construction, their reliance on strong-form loss formulations makes them highly sensitive to measurement noise. To address this limitation, we propose weak formulation-based GENERIC formalism informed neural networks (WGFINNs), which integrate the weak formulation of dynamical systems with the structure-preserving architecture of GFINNs. WGFINNs significantly enhance robustness to noisy data while retaining exact satisfaction of GENERIC degeneracy and symmetry conditions. We further incorporate a state-wise weighted loss and a residual-based attention mechanism to mitigate scale imbalance across state variables. Theoretical analysis contrasts quantitative differences between the strong-form and the weak-form estimators. Mainly, the strong-form estimator diverges as the time step decreases in the presence of noise, while the weak-form estimator can be accurate even with noisy data if test functions satisfy certain conditions. Numerical experiments demonstrate that WGFINNs consistently outperform GFINNs at varying noise levels, achieving more accurate predictions and reliable recovery of physical quantities.

tLaSDI: Thermodynamics-informed latent space dynamics identification

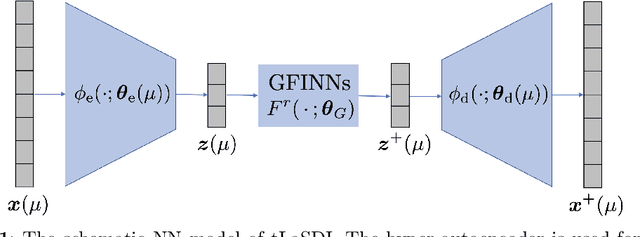
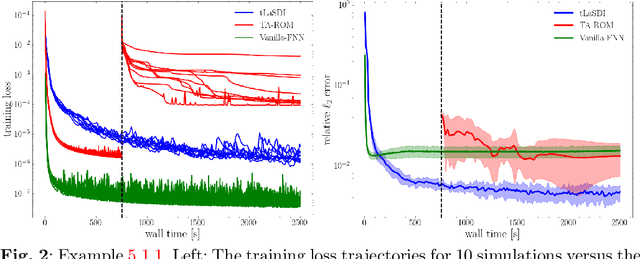
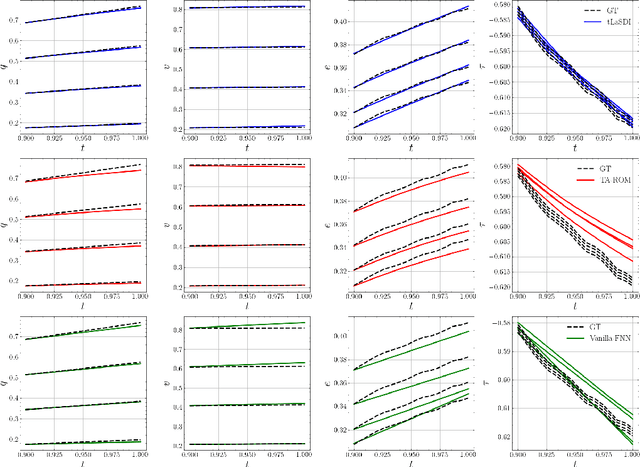
We propose a data-driven latent space dynamics identification method (tLaSDI) that embeds the first and second principles of thermodynamics. The latent variables are learned through an autoencoder as a nonlinear dimension reduction model. The dynamics of the latent variables are constructed by a neural network-based model that preserves certain structures to respect the thermodynamic laws through the GENERIC formalism. An abstract error estimate of the approximation is established, which provides a new loss formulation involving the Jacobian computation of autoencoder. Both the autoencoder and the latent dynamics are trained to minimize the new loss. Numerical examples are presented to demonstrate the performance of tLaSDI, which exhibits robust generalization ability, even in extrapolation. In addition, an intriguing correlation is empirically observed between the entropy production rates in the latent space and the behaviors of the full-state solution.