Yeonjong Shin
Thermodynamically Consistent Latent Dynamics Identification for Parametric Systems
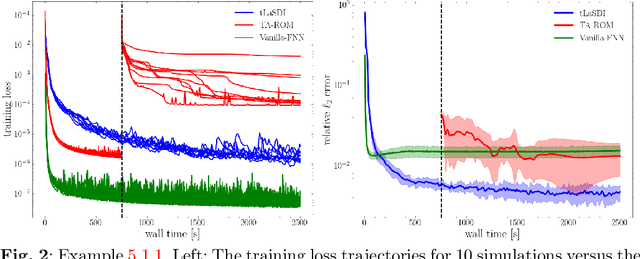
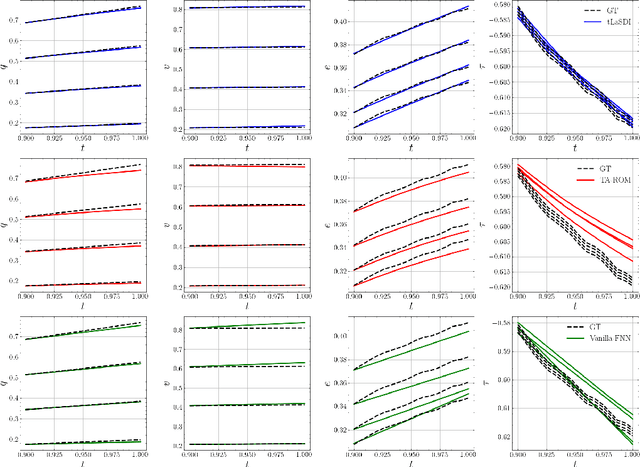
Jun 10, 2025Abstract:We propose an efficient thermodynamics-informed latent space dynamics identification (tLaSDI) framework for the reduced-order modeling of parametric nonlinear dynamical systems. This framework integrates autoencoders for dimensionality reduction with newly developed parametric GENERIC formalism-informed neural networks (pGFINNs), which enable efficient learning of parametric latent dynamics while preserving key thermodynamic principles such as free energy conservation and entropy generation across the parameter space. To further enhance model performance, a physics-informed active learning strategy is incorporated, leveraging a greedy, residual-based error indicator to adaptively sample informative training data, outperforming uniform sampling at equivalent computational cost. Numerical experiments on the Burgers' equation and the 1D/1V Vlasov-Poisson equation demonstrate that the proposed method achieves up to 3,528x speed-up with 1-3% relative errors, and significant reduction in training (50-90%) and inference (57-61%) cost. Moreover, the learned latent space dynamics reveal the underlying thermodynamic behavior of the system, offering valuable insights into the physical-space dynamics.
A Comprehensive Review of Latent Space Dynamics Identification Algorithms for Intrusive and Non-Intrusive Reduced-Order-Modeling
Mar 16, 2024
Abstract:Numerical solvers of partial differential equations (PDEs) have been widely employed for simulating physical systems. However, the computational cost remains a major bottleneck in various scientific and engineering applications, which has motivated the development of reduced-order models (ROMs). Recently, machine-learning-based ROMs have gained significant popularity and are promising for addressing some limitations of traditional ROM methods, especially for advection dominated systems. In this chapter, we focus on a particular framework known as Latent Space Dynamics Identification (LaSDI), which transforms the high-fidelity data, governed by a PDE, to simpler and low-dimensional latent-space data, governed by ordinary differential equations (ODEs). These ODEs can be learned and subsequently interpolated to make ROM predictions. Each building block of LaSDI can be easily modulated depending on the application, which makes the LaSDI framework highly flexible. In particular, we present strategies to enforce the laws of thermodynamics into LaSDI models (tLaSDI), enhance robustness in the presence of noise through the weak form (WLaSDI), select high-fidelity training data efficiently through active learning (gLaSDI, GPLaSDI), and quantify the ROM prediction uncertainty through Gaussian processes (GPLaSDI). We demonstrate the performance of different LaSDI approaches on Burgers equation, a non-linear heat conduction problem, and a plasma physics problem, showing that LaSDI algorithms can achieve relative errors of less than a few percent and up to thousands of times speed-ups.
tLaSDI: Thermodynamics-informed latent space dynamics identification
Mar 09, 2024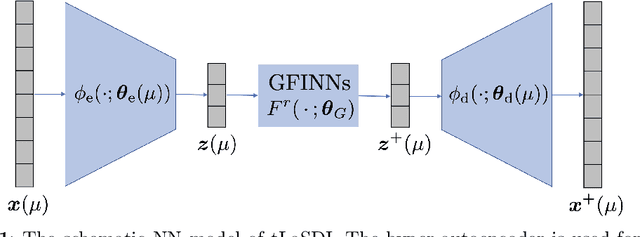

Abstract:We propose a data-driven latent space dynamics identification method (tLaSDI) that embeds the first and second principles of thermodynamics. The latent variables are learned through an autoencoder as a nonlinear dimension reduction model. The dynamics of the latent variables are constructed by a neural network-based model that preserves certain structures to respect the thermodynamic laws through the GENERIC formalism. An abstract error estimate of the approximation is established, which provides a new loss formulation involving the Jacobian computation of autoencoder. Both the autoencoder and the latent dynamics are trained to minimize the new loss. Numerical examples are presented to demonstrate the performance of tLaSDI, which exhibits robust generalization ability, even in extrapolation. In addition, an intriguing correlation is empirically observed between the entropy production rates in the latent space and the behaviors of the full-state solution.
Randomized Forward Mode of Automatic Differentiation for Optimization Algorithms
Oct 24, 2023Abstract:Backpropagation within neural networks leverages a fundamental element of automatic differentiation, which is referred to as the reverse mode differentiation, or vector Jacobian Product (VJP) or, in the context of differential geometry, known as the pull-back process. The computation of gradient is important as update of neural network parameters is performed using gradient descent method. In this study, we present a genric randomized method, which updates the parameters of neural networks by using directional derivatives of loss functions computed efficiently by using forward mode AD or Jacobian vector Product (JVP). These JVP are computed along the random directions sampled from different probability distributions e.g., Bernoulli, Normal, Wigner, Laplace and Uniform distributions. The computation of gradient is performed during the forward pass of the neural network. We also present a rigorous analysis of the presented methods providing the rate of convergence along with the computational experiments deployed in scientific Machine learning in particular physics-informed neural networks and Deep Operator Networks.
On the training and generalization of deep operator networks
Sep 02, 2023Abstract:We present a novel training method for deep operator networks (DeepONets), one of the most popular neural network models for operators. DeepONets are constructed by two sub-networks, namely the branch and trunk networks. Typically, the two sub-networks are trained simultaneously, which amounts to solving a complex optimization problem in a high dimensional space. In addition, the nonconvex and nonlinear nature makes training very challenging. To tackle such a challenge, we propose a two-step training method that trains the trunk network first and then sequentially trains the branch network. The core mechanism is motivated by the divide-and-conquer paradigm and is the decomposition of the entire complex training task into two subtasks with reduced complexity. Therein the Gram-Schmidt orthonormalization process is introduced which significantly improves stability and generalization ability. On the theoretical side, we establish a generalization error estimate in terms of the number of training data, the width of DeepONets, and the number of input and output sensors. Numerical examples are presented to demonstrate the effectiveness of the two-step training method, including Darcy flow in heterogeneous porous media.
GFINNs: GENERIC Formalism Informed Neural Networks for Deterministic and Stochastic Dynamical Systems
Aug 31, 2021

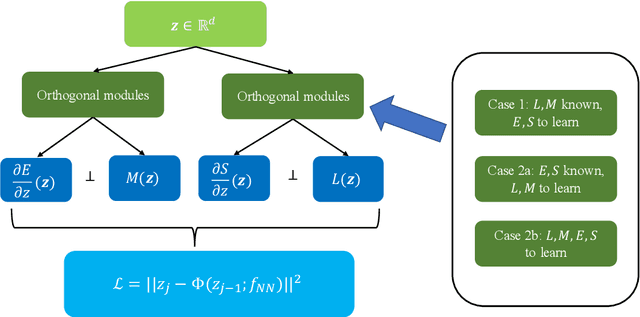
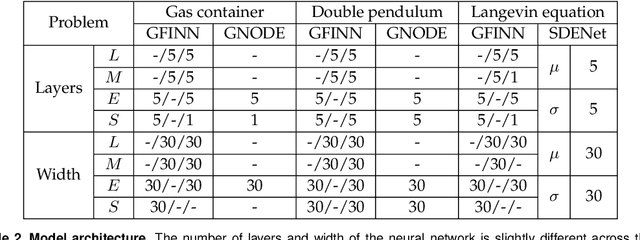
Abstract:We propose the GENERIC formalism informed neural networks (GFINNs) that obey the symmetric degeneracy conditions of the GENERIC formalism. GFINNs comprise two modules, each of which contains two components. We model each component using a neural network whose architecture is designed to satisfy the required conditions. The component-wise architecture design provides flexible ways of leveraging available physics information into neural networks. We prove theoretically that GFINNs are sufficiently expressive to learn the underlying equations, hence establishing the universal approximation theorem. We demonstrate the performance of GFINNs in three simulation problems: gas containers exchanging heat and volume, thermoelastic double pendulum and the Langevin dynamics. In all the examples, GFINNs outperform existing methods, hence demonstrating good accuracy in predictions for both deterministic and stochastic systems.
Deep Kronecker neural networks: A general framework for neural networks with adaptive activation functions
May 20, 2021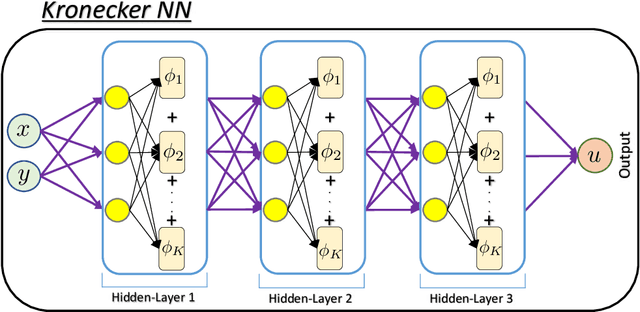

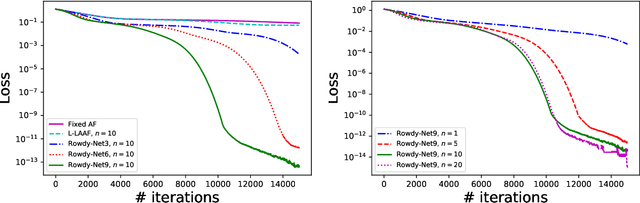

Abstract:We propose a new type of neural networks, Kronecker neural networks (KNNs), that form a general framework for neural networks with adaptive activation functions. KNNs employ the Kronecker product, which provides an efficient way of constructing a very wide network while keeping the number of parameters low. Our theoretical analysis reveals that under suitable conditions, KNNs induce a faster decay of the loss than that by the feed-forward networks. This is also empirically verified through a set of computational examples. Furthermore, under certain technical assumptions, we establish global convergence of gradient descent for KNNs. As a specific case, we propose the Rowdy activation function that is designed to get rid of any saturation region by injecting sinusoidal fluctuations, which include trainable parameters. The proposed Rowdy activation function can be employed in any neural network architecture like feed-forward neural networks, Recurrent neural networks, Convolutional neural networks etc. The effectiveness of KNNs with Rowdy activation is demonstrated through various computational experiments including function approximation using feed-forward neural networks, solution inference of partial differential equations using the physics-informed neural networks, and standard deep learning benchmark problems using convolutional and fully-connected neural networks.
A Caputo fractional derivative-based algorithm for optimization
Apr 06, 2021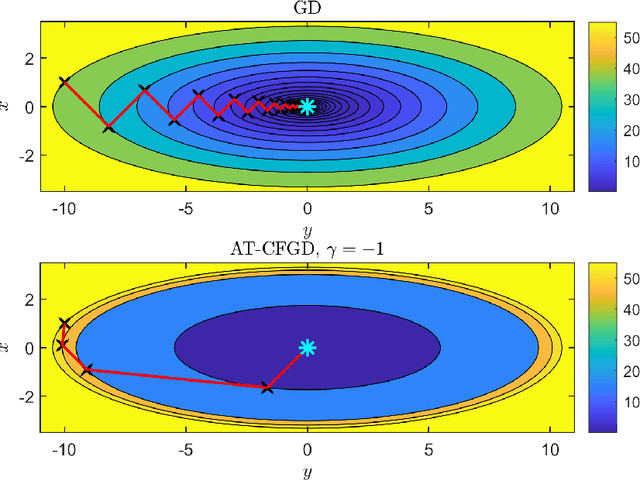

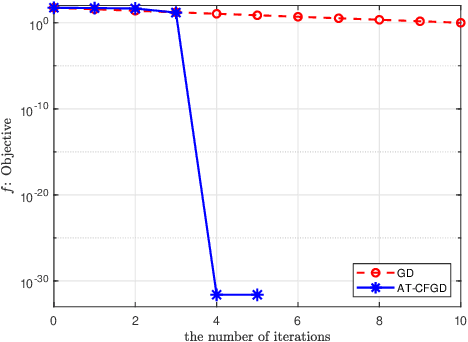
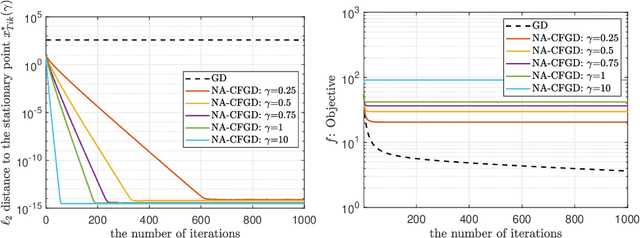
Abstract:We propose a novel Caputo fractional derivative-based optimization algorithm. Upon defining the Caputo fractional gradient with respect to the Cartesian coordinate, we present a generic Caputo fractional gradient descent (CFGD) method. We prove that the CFGD yields the steepest descent direction of a locally smoothed objective function. The generic CFGD requires three parameters to be specified, and a choice of the parameters yields a version of CFGD. We propose three versions -- non-adaptive, adaptive terminal and adaptive order. By focusing on quadratic objective functions, we provide a convergence analysis. We prove that the non-adaptive CFGD converges to a Tikhonov regularized solution. For the two adaptive versions, we derive error bounds, which show convergence to integer-order stationary point under some conditions. We derive an explicit formula of CFGD for quadratic functions. We computationally found that the adaptive terminal (AT) CFGD mitigates the dependence on the condition number in the rate of convergence and results in significant acceleration over gradient descent (GD). For non-quadratic functions, we develop an efficient implementation of CFGD using the Gauss-Jacobi quadrature, whose computational cost is approximately proportional to the number of the quadrature points and the cost of GD. Our numerical examples show that AT-CFGD results in acceleration over GD, even when a small number of the Gauss-Jacobi quadrature points (including a single point) is used.
Plateau Phenomenon in Gradient Descent Training of ReLU networks: Explanation, Quantification and Avoidance
Jul 14, 2020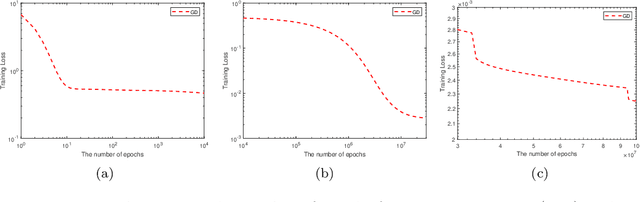
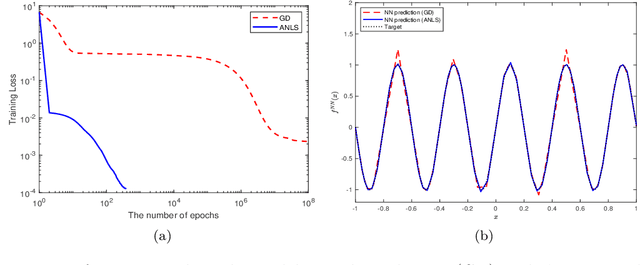
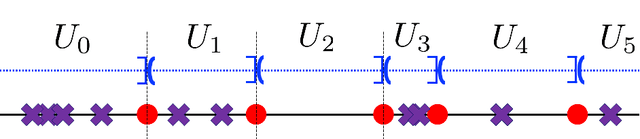
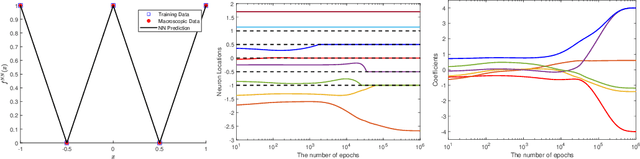
Abstract:The ability of neural networks to provide `best in class' approximation across a wide range of applications is well-documented. Nevertheless, the powerful expressivity of neural networks comes to naught if one is unable to effectively train (choose) the parameters defining the network. In general, neural networks are trained by gradient descent type optimization methods, or a stochastic variant thereof. In practice, such methods result in the loss function decreases rapidly at the beginning of training but then, after a relatively small number of steps, significantly slow down. The loss may even appear to stagnate over the period of a large number of epochs, only to then suddenly start to decrease fast again for no apparent reason. This so-called plateau phenomenon manifests itself in many learning tasks. The present work aims to identify and quantify the root causes of plateau phenomenon. No assumptions are made on the number of neurons relative to the number of training data, and our results hold for both the lazy and adaptive regimes. The main findings are: plateaux correspond to periods during which activation patterns remain constant, where activation pattern refers to the number of data points that activate a given neuron; quantification of convergence of the gradient flow dynamics; and, characterization of stationary points in terms solutions of local least squares regression lines over subsets of the training data. Based on these conclusions, we propose a new iterative training method, the Active Neuron Least Squares (ANLS), characterised by the explicit adjustment of the activation pattern at each step, which is designed to enable a quick exit from a plateau. Illustrative numerical examples are included throughout.
On the Convergence and generalization of Physics Informed Neural Networks
Apr 03, 2020
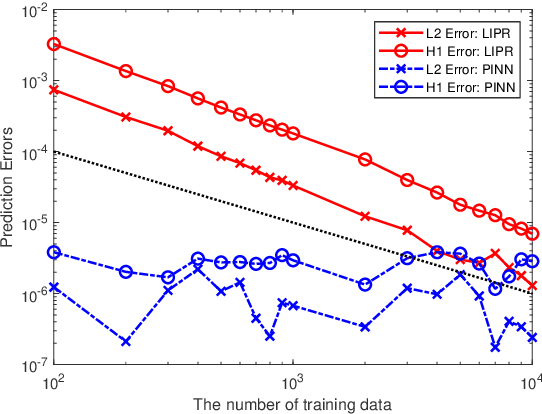
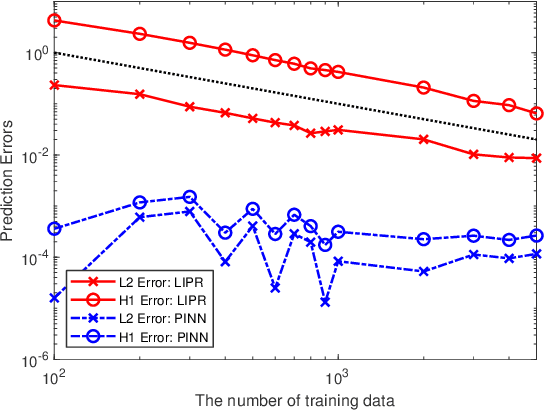
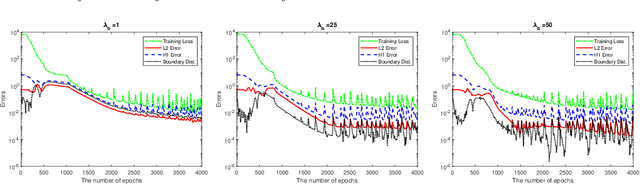
Abstract:Physics informed neural networks (PINNs) are deep learning based techniques for solving partial differential equations (PDEs). Guided by data and physical laws, PINNs find a neural network that approximates the solution to a system of PDEs. Such a neural network is obtained by minimizing a loss function in which any prior knowledge of PDEs and data are encoded. Despite its remarkable empirical success, there is little theoretical justification for PINNs. In this paper, we establish a mathematical foundation of the PINNs methodology. As the number of data grows, PINNs generate a sequence of minimizers which correspond to a sequence of neural networks. We want to answer the question: Does the sequence of minimizers converge to the solution to the PDE? This question is also related to the generalization of PINNs. We consider two classes of PDEs: elliptic and parabolic. By adapting the Schuader approach, we show that the sequence of minimizers strongly converges to the PDE solution in $L^2$. Furthermore, we show that if each minimizer satisfies the initial/boundary conditions, the convergence mode can be improved to $H^1$. Computational examples are provided to illustrate our theoretical findings. To the best of our knowledge, this is the first theoretical work that shows the consistency of the PINNs methodology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge