Deep Kronecker neural networks: A general framework for neural networks with adaptive activation functions
Paper and Code
May 20, 2021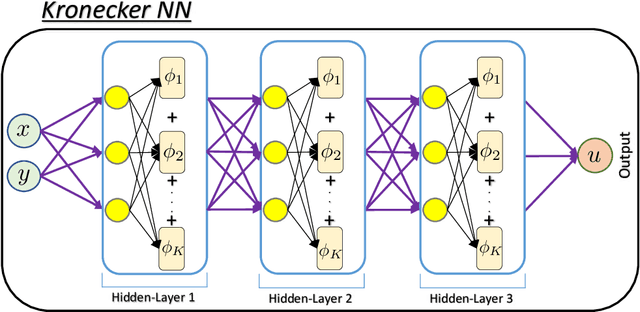

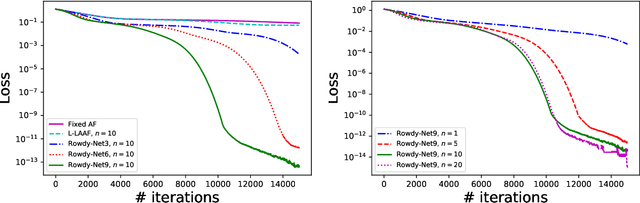

We propose a new type of neural networks, Kronecker neural networks (KNNs), that form a general framework for neural networks with adaptive activation functions. KNNs employ the Kronecker product, which provides an efficient way of constructing a very wide network while keeping the number of parameters low. Our theoretical analysis reveals that under suitable conditions, KNNs induce a faster decay of the loss than that by the feed-forward networks. This is also empirically verified through a set of computational examples. Furthermore, under certain technical assumptions, we establish global convergence of gradient descent for KNNs. As a specific case, we propose the Rowdy activation function that is designed to get rid of any saturation region by injecting sinusoidal fluctuations, which include trainable parameters. The proposed Rowdy activation function can be employed in any neural network architecture like feed-forward neural networks, Recurrent neural networks, Convolutional neural networks etc. The effectiveness of KNNs with Rowdy activation is demonstrated through various computational experiments including function approximation using feed-forward neural networks, solution inference of partial differential equations using the physics-informed neural networks, and standard deep learning benchmark problems using convolutional and fully-connected neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge