Neural Functions for Learning Periodic Signal

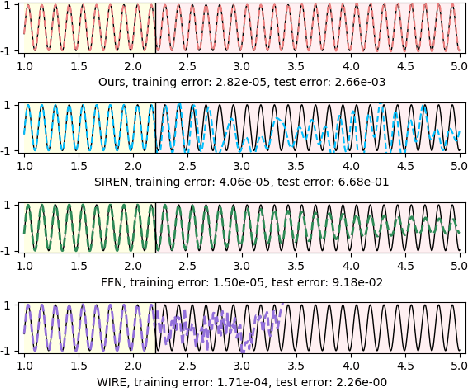
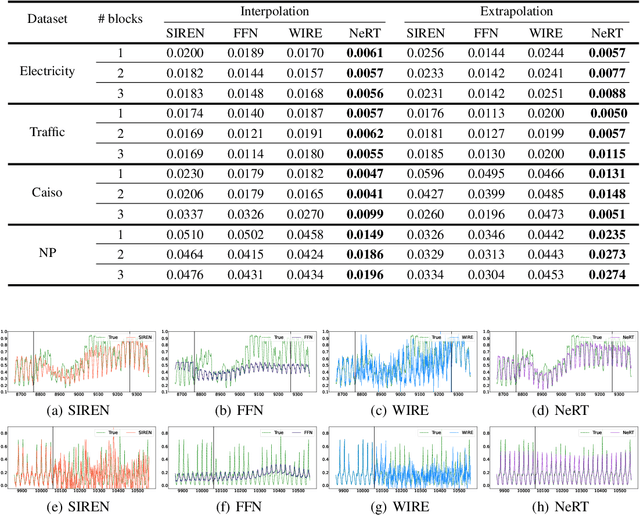
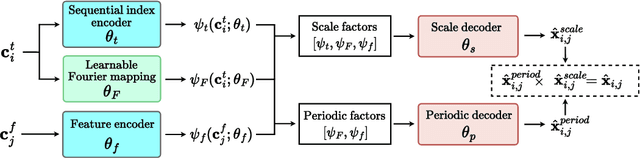
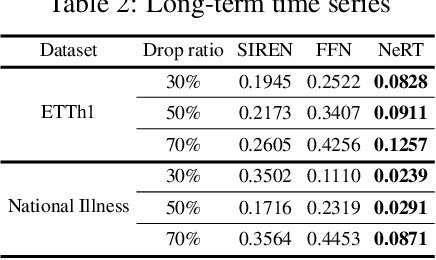
As function approximators, deep neural networks have served as an effective tool to represent various signal types. Recent approaches utilize multi-layer perceptrons (MLPs) to learn a nonlinear mapping from a coordinate to its corresponding signal, facilitating the learning of continuous neural representations from discrete data points. Despite notable successes in learning diverse signal types, coordinate-based MLPs often face issues of overfitting and limited generalizability beyond the training region, resulting in subpar extrapolation performance. This study addresses scenarios where the underlying true signals exhibit periodic properties, either spatially or temporally. We propose a novel network architecture, which extracts periodic patterns from measurements and leverages this information to represent the signal, thereby enhancing generalization and improving extrapolation performance. We demonstrate the efficacy of the proposed method through comprehensive experiments, including the learning of the periodic solutions for differential equations, and time series imputation (interpolation) and forecasting (extrapolation) on real-world datasets.

Thermodynamically Consistent Latent Dynamics Identification for Parametric Systems

We propose an efficient thermodynamics-informed latent space dynamics identification (tLaSDI) framework for the reduced-order modeling of parametric nonlinear dynamical systems. This framework integrates autoencoders for dimensionality reduction with newly developed parametric GENERIC formalism-informed neural networks (pGFINNs), which enable efficient learning of parametric latent dynamics while preserving key thermodynamic principles such as free energy conservation and entropy generation across the parameter space. To further enhance model performance, a physics-informed active learning strategy is incorporated, leveraging a greedy, residual-based error indicator to adaptively sample informative training data, outperforming uniform sampling at equivalent computational cost. Numerical experiments on the Burgers' equation and the 1D/1V Vlasov-Poisson equation demonstrate that the proposed method achieves up to 3,528x speed-up with 1-3% relative errors, and significant reduction in training (50-90%) and inference (57-61%) cost. Moreover, the learned latent space dynamics reveal the underlying thermodynamic behavior of the system, offering valuable insights into the physical-space dynamics.

PIORF: Physics-Informed Ollivier-Ricci Flow for Long-Range Interactions in Mesh Graph Neural Networks

Recently, data-driven simulators based on graph neural networks have gained attention in modeling physical systems on unstructured meshes. However, they struggle with long-range dependencies in fluid flows, particularly in refined mesh regions. This challenge, known as the 'over-squashing' problem, hinders information propagation. While existing graph rewiring methods address this issue to some extent, they only consider graph topology, overlooking the underlying physical phenomena. We propose Physics-Informed Ollivier-Ricci Flow (PIORF), a novel rewiring method that combines physical correlations with graph topology. PIORF uses Ollivier-Ricci curvature (ORC) to identify bottleneck regions and connects these areas with nodes in high-velocity gradient nodes, enabling long-range interactions and mitigating over-squashing. Our approach is computationally efficient in rewiring edges and can scale to larger simulations. Experimental results on 3 fluid dynamics benchmark datasets show that PIORF consistently outperforms baseline models and existing rewiring methods, achieving up to 26.2 improvement.

Unveiling the Potential of Superexpressive Networks in Implicit Neural Representations

In this study, we examine the potential of one of the ``superexpressive'' networks in the context of learning neural functions for representing complex signals and performing machine learning downstream tasks. Our focus is on evaluating their performance on computer vision and scientific machine learning tasks including signal representation/inverse problems and solutions of partial differential equations. Through an empirical investigation in various benchmark tasks, we demonstrate that superexpressive networks, as proposed by [Zhang et al. NeurIPS, 2022], which employ a specialized network structure characterized by having an additional dimension, namely width, depth, and ``height'', can surpass recent implicit neural representations that use highly-specialized nonlinear activation functions.

Understanding and Mitigating Membership Inference Risks of Neural Ordinary Differential Equations

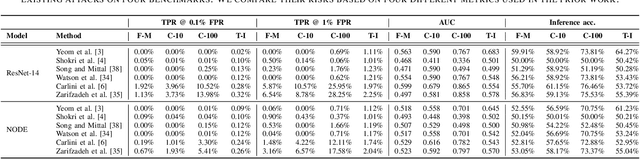
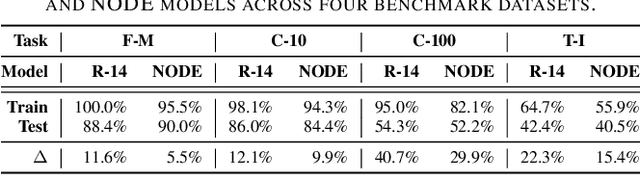
Neural ordinary differential equations (NODEs) are an emerging paradigm in scientific computing for modeling dynamical systems. By accurately learning underlying dynamics in data in the form of differential equations, NODEs have been widely adopted in various domains, such as healthcare, finance, computer vision, and language modeling. However, there remains a limited understanding of the privacy implications of these fundamentally different models, particularly with regard to their membership inference risks. In this work, we study the membership inference risks associated with NODEs. We first comprehensively evaluate NODEs against membership inference attacks. We show that NODEs are twice as resistant to these privacy attacks compared to conventional feedforward models such as ResNets. By analyzing the variance in membership risks across different NODE models, we identify the factors that contribute to their lower risks. We then demonstrate, both theoretically and empirically, that membership inference risks can be further mitigated by utilizing a stochastic variant of NODEs: Neural stochastic differential equations (NSDEs). We show that NSDEs are differentially-private (DP) learners that provide the same provable privacy guarantees as DP-SGD, the de-facto mechanism for training private models. NSDEs are also effective in mitigating existing membership inference attacks, demonstrating risks comparable to private models trained with DP-SGD while offering an improved privacy-utility trade-off. Moreover, we propose a drop-in-replacement strategy that efficiently integrates NSDEs into conventional feedforward models to enhance their privacy.

Physics-informed reduced order model with conditional neural fields

This study presents the conditional neural fields for reduced-order modeling (CNF-ROM) framework to approximate solutions of parametrized partial differential equations (PDEs). The approach combines a parametric neural ODE (PNODE) for modeling latent dynamics over time with a decoder that reconstructs PDE solutions from the corresponding latent states. We introduce a physics-informed learning objective for CNF-ROM, which includes two key components. First, the framework uses coordinate-based neural networks to calculate and minimize PDE residuals by computing spatial derivatives via automatic differentiation and applying the chain rule for time derivatives. Second, exact initial and boundary conditions (IC/BC) are imposed using approximate distance functions (ADFs) [Sukumar and Srivastava, CMAME, 2022]. However, ADFs introduce a trade-off as their second- or higher-order derivatives become unstable at the joining points of boundaries. To address this, we introduce an auxiliary network inspired by [Gladstone et al., NeurIPS ML4PS workshop, 2022]. Our method is validated through parameter extrapolation and interpolation, temporal extrapolation, and comparisons with analytical solutions.

MaD-Scientist: AI-based Scientist solving Convection-Diffusion-Reaction Equations Using Massive PINN-Based Prior Data

Large language models (LLMs), like ChatGPT, have shown that even trained with noisy prior data, they can generalize effectively to new tasks through in-context learning (ICL) and pre-training techniques. Motivated by this, we explore whether a similar approach can be applied to scientific foundation models (SFMs). Our methodology is structured as follows: (i) we collect low-cost physics-informed neural network (PINN)-based approximated prior data in the form of solutions to partial differential equations (PDEs) constructed through an arbitrary linear combination of mathematical dictionaries; (ii) we utilize Transformer architectures with self and cross-attention mechanisms to predict PDE solutions without knowledge of the governing equations in a zero-shot setting; (iii) we provide experimental evidence on the one-dimensional convection-diffusion-reaction equation, which demonstrate that pre-training remains robust even with approximated prior data, with only marginal impacts on test accuracy. Notably, this finding opens the path to pre-training SFMs with realistic, low-cost data instead of (or in conjunction with) numerical high-cost data. These results support the conjecture that SFMs can improve in a manner similar to LLMs, where fully cleaning the vast set of sentences crawled from the Internet is nearly impossible.

FastLRNR and Sparse Physics Informed Backpropagation

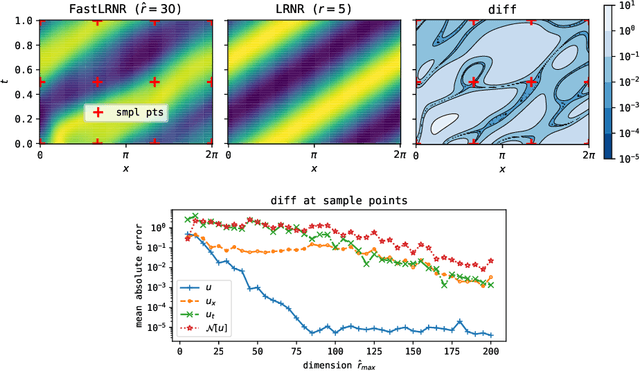
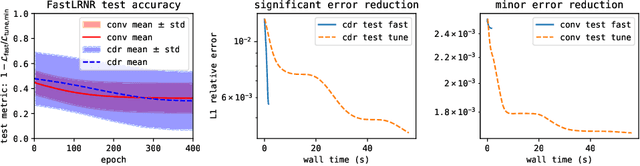
We introduce Sparse Physics Informed Backpropagation (SPInProp), a new class of methods for accelerating backpropagation for a specialized neural network architecture called Low Rank Neural Representation (LRNR). The approach exploits the low rank structure within LRNR and constructs a reduced neural network approximation that is much smaller in size. We call the smaller network FastLRNR. We show that backpropagation of FastLRNR can be substituted for that of LRNR, enabling a significant reduction in complexity. We apply SPInProp to a physics informed neural networks framework and demonstrate how the solution of parametrized partial differential equations is accelerated.

Latent Space Energy-based Neural ODEs

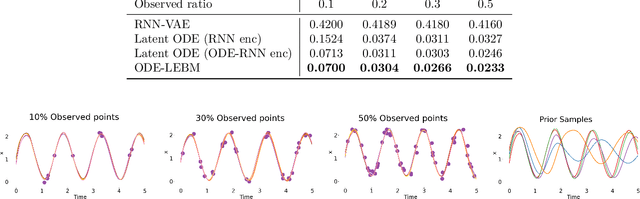
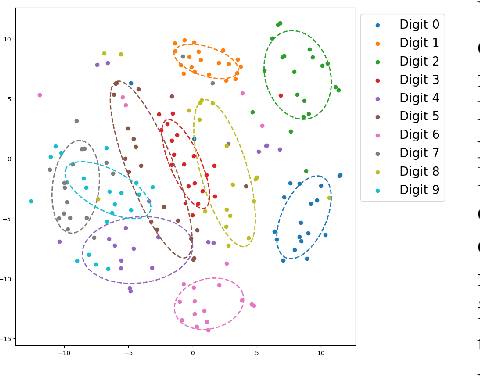
This paper introduces a novel family of deep dynamical models designed to represent continuous-time sequence data. This family of models generates each data point in the time series by a neural emission model, which is a non-linear transformation of a latent state vector. The trajectory of the latent states is implicitly described by a neural ordinary differential equation (ODE), with the initial state following an informative prior distribution parameterized by an energy-based model. Furthermore, we can extend this model to disentangle dynamic states from underlying static factors of variation, represented as time-invariant variables in the latent space. We train the model using maximum likelihood estimation with Markov chain Monte Carlo (MCMC) in an end-to-end manner, without requiring additional assisting components such as an inference network. Our experiments on oscillating systems, videos and real-world state sequences (MuJoCo) illustrate that ODEs with the learnable energy-based prior outperform existing counterparts, and can generalize to new dynamic parameterization, enabling long-horizon predictions.

Parameterized Physics-informed Neural Networks for Parameterized PDEs

Complex physical systems are often described by partial differential equations (PDEs) that depend on parameters such as the Reynolds number in fluid mechanics. In applications such as design optimization or uncertainty quantification, solutions of those PDEs need to be evaluated at numerous points in the parameter space. While physics-informed neural networks (PINNs) have emerged as a new strong competitor as a surrogate, their usage in this scenario remains underexplored due to the inherent need for repetitive and time-consuming training. In this paper, we address this problem by proposing a novel extension, parameterized physics-informed neural networks (P$^2$INNs). P$^2$INNs enable modeling the solutions of parameterized PDEs via explicitly encoding a latent representation of PDE parameters. With the extensive empirical evaluation, we demonstrate that P$^2$INNs outperform the baselines both in accuracy and parameter efficiency on benchmark 1D and 2D parameterized PDEs and are also effective in overcoming the known "failure modes".